大带宽通信压缩域干扰抑制方法综述

张永顺，朱卫纲，贾 鑫，詹亚云

(1.航天工程大学 电子与光学工程系，北京 101416；2.航天工程大学 研究生院，北京 101416；3.空军指挥学院 研究生大队，北京 10089)

近几十年来，信息技术突飞猛进，人们对信息量的需求不断增加。为了满足人们日益增加的信息需求，除了通信信号体制创新之外，通信系统的传输速率和带宽急剧增加。经典的信号采集处理理论以Shannon-Nyqust采样定理为基础，要求采样速率为信号最高频率或者信号带宽的两倍。这一限制使得基于Shannon-Nyquist采样定理的宽带信号处理面临信号采集代价过高的问题，有时甚至出现采样速率无法达到系统要求的情况。此外，即使付出较大代价实现信号采样后，高速采集的信号往往包含冗余，不利于后续信号的存储、传输和实时处理。近年来兴起的压缩感知(Compressive Sensing,CS)理论为解决大带宽信号的采集问题提供了一条可行的途径。该理论指出，当接收信号为稀疏信号或可压缩信号时，接收端能以远低于Nyquist-Shannon采样理论要求的速率对信号进行采样，并通过系统后端的数字处理算法准确地恢复出原信号。目前，很多学者将CS理论应用于宽带信号采集和处理，取得了大量的研究成果[1-3]。

信息量需求的激增使得自由空间传播的无线电信号急剧增加，无线通信面临的电磁环境日益复杂，各种无意或有意干扰对通信的有效性和可靠性构成了严重的挑战。大带宽通信系统由于系统接收机通带较宽更易受到各种干扰的影响，需要使用干扰抑制技术才能实现可靠通信。然而，应用CS理论虽然能够有效降低大带宽通信系统的采样速率，也带来了一个显著的问题，即压缩信号虽然保留了原信号的结构信息，但其特性相比于Nyquist-Shannon采样信号已经发生明显变化[4]，这使得传统的通信干扰抑制技术不再适用，而没有有效的干扰抑制技术将导致干扰条件下信号无法有效重构。因此，研究大带宽通信压缩域干扰抑制技术显得很有必要。

目前，国内外关于压缩域干扰抑制方法的研究方兴未艾，公开报道了很多研究成果，但是对压缩域干扰抑制方法的综述文章还未见报道。本文主要针对大带宽通信压缩域干扰抑制研究的相关问题进行分析总结。压缩域干扰抑制研究主要涉及3个方面的问题：压缩域干扰检测问题；压缩域干扰参数估计问题；压缩域干扰抑制问题。本文将对上述三方面问题的研究现状分别进行分析概括。同时，对可能用于上述3个方面问题解决的方法的研究现状也进行总结分析。在分析现有研究成果优势与不足的基础上，进一步展望未来需要重点研究的问题。需要指出的是本文中的大带宽通信主要指的是民用通信中常见的正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)通信以及军用通信中常见的扩谱通信。

1 CS理论简介

设任意N维信号s=[s1,s2,s3,…,sN]T∈RN或CN，满足

(1)

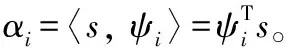
CS信号获取数学模型可以表示为

y=Φs=ΦΨα

(2)

式中，Φ∈RM×N或Φ∈CM×N表示大小为M×N的随机测量矩阵；y∈RM或y∈CM表示长度为M的压缩信号。此处，压缩信号的长度小于输入信号的长度，即M

重构算法的输入即压缩信号y和感知矩阵Θ，其中Θ=ΦΨ∈RM×N或Θ=ΦΨ∈CM×N。通过求解式(2)的逆即可实现从压缩信号中重构出原始信号，但由于M

(3)

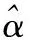
式(3)被证明是非确定性多项式(Non-deterministic Polynomial,NP)难问题[8]。因此，通常情况下将式(3)转化为式(4)所示的可使用凸优化方法进行求解的最小化l1范数问题：

(4)

2 压缩域干扰检测

干扰检测能够为干扰抑制提供必要的先验信息，降低干扰抑制算法的复杂度，进一步提高干扰抑制算法的性能。压缩域干扰检测就是利用干扰信号的稀疏特性，从压缩采样数据中获取干扰信息，完成干扰检测的任务。相比于干扰重构，压缩域干扰检测所需的压缩测量值更少。

文献[9]将压缩域干扰检测建模为如式(5)所示的二元假设问题。

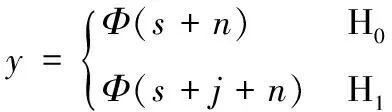
(5)

式中:s表示发送信号；n表示背景噪声，通常建模为高斯白噪声；j为待检测的干扰。根据上述模型，若干扰存在判定为H1，否则判定为H0。

由于信号和干扰通常具有不同的稀疏特性，这使得干扰和信号在压缩域是可分的，例如，干扰和信号不能在同一字典上得到稀疏表示或者虽然干扰和信号能在同一字典得到稀疏表示，但干扰稀疏系数向量和信号稀疏系数向量之间具有明显可分的特征。压缩域干扰检测即利用这种可分性在有用信号和噪声存在的条件下，利用压缩信号实现干扰检测的目的。文献[9]利用正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法内积搜索阶段中获取最大相关性列向量的思想，提出了基于OMP和单元平均恒虚警(Cell Average Constant False Alarm Rate,CA-CFAR)检测的直扩(Direct Sequence Spread Spectrum,DSSS)通信压缩域干扰检测方法。该方法只利用一次内积运算即可获取干扰检测的特征值，算法计算量小，并且由于利用CFAR检测技术对特征量进行检测，算法能够实现自适应的干扰检测。该方法的不足之处是要求干扰在其稀疏字典上具有高度稀疏性。由于具有的一定带宽的窄带干扰(Narrowband Interference,NBI)在频域的稀疏性较差，文献[9]中提出的方法对NBI的检测性能较差。文献[10]针对这一不足，详细分析了NBI的频域块稀疏性，提出了基于块稀疏贝叶斯学习(Block Sparse Bayesian Learning,BSBL)的DSSS通信NBI检测方法。该方法能够实现对具有一定带宽的NBI的有效检测。但该算法在干扰检测中需要对NBI进行部分重构，算法较为复杂，并且由于BSBL算法运算效率较低，导致该算法的时效性较差。

目前压缩域干扰检测方法研究的文献仍然较少，利用大带宽通信信号的功率平坦特性，可行的解决思路是将压缩域信号检测方法应用到大带宽通信压缩域干扰检测，并结合干扰特性进行相应的改进。目前，压缩域信号检测方法大致可以分为以下几类：基于部分重构的压缩域信号检测方法[11]；基于信号概率分布模型的压缩域信号检测方法[12]；基于信号循环平稳特性的压缩域信号检测方法[13]。

3 压缩域干扰参数估计

3.1 稀疏度估计

稀疏度信息的获取被认为是CS理论与实用之间一个需要重点解决的问题。在大多数算法中，通常假设信号稀疏度是已知的，但实际系统中，干扰稀疏度信息对于接收端而言是未知的。为解决稀疏度未知条件下信号的重构问题，学者们提出了不依赖稀疏度信息的信号重构算法，比如稀疏度自适应匹配追踪算法[14]，但是该类算法在噪声环境下性能较差，不适用于干扰重构。此外，一种常见的解决方案是用统计意义下的最大稀疏度Kmax代替实际稀疏度K，而Kmax与K之间的差异必然会带来不必要采样开销。目前，关于干扰稀疏度估计问题研究的文献仍然相对较少，研究具有低复杂度的、快速的干扰稀疏度估计方法是压缩域干扰抑制研究需要亟待解决的一个问题。利用大带宽信号功率谱平坦的特性，可行的解决思路是将现有的信号稀疏度估计算法应用于干扰稀疏度的估计。已有信号稀疏度估计方法可以分为以下几类：

1)基于信号重构的稀疏度估计方法。文献[15]首次提出了稀疏度估计这一概念，并提出了一种两步稀疏度估计算法。该算法首先利用较少的采样点数估计稀疏度，然后利用稀疏度估计值自适应调整采样速率。该算法的不足是稀疏度估计主要基于Monte-Carlo模拟和曲线拟合方法，缺乏理论分析，且算法需要重构原始信号，计算复杂度较高。文献[16]提出一种利用序列采样估计稀疏度的算法。该算法通过逐次递增观测次数，直至信号重建结果收敛。但由于需要反复重构原始信号，故算法计算复杂度较高。文献[17]表明可以从信号重构中估计稀疏度，并证明了估计稀疏度所需的压缩测量值的理论上限。但该理论上限只能使用数值的方法获取并且信号重构中需要解决复杂的优化问题。

2)基于测量矩阵的稀疏度估计方法。文献[18]表明，由柯西和高斯分布式测量矩阵组成的测量矩阵能够利用信号的l1范数和l2范数实现对稀疏度的连续测量。但是，此度量只是稀疏度的近似结果，与信号真实的稀疏度并不完全相等[19]。此外，该方法对测量矩阵的组成要求非常严格。文献[20]提出使用稀疏测量矩阵估计信号稀疏度的算法。使用该算法得到的稀疏度估计器复杂度较低。但该算法对测量矩阵的非相干性要求较高，并且该算法只适用于信号维度较大的情况，对于维度较低的信号的稀疏度估计不适用。文献[21]利用构造的具有Khatri-Rao结构的测量矩阵对信号进行压缩采样，将稀疏度估计问题转换为测量向量的重新排列的矩阵的秩估计问题进行求解，算法不需要重构原始信号，算法复杂度较低。但该算法同样存在对测量矩阵的非相干性要求较高的问题。

3)基于信号协方差矩阵的稀疏度估计方法。文献[19]利用渐近随机矩阵理论提出了一种基于特征值的信号稀疏度估计算法。针对多重测量向量稀疏度估计问题，建立了信号稀疏度和压缩信号协方差矩阵的秩之间的联系，通过估计压缩信号协方差矩阵的秩实现对信号稀疏度的估计。但该算法在实现过程中需要兼顾信号的平稳性以及稀疏表示系数的时变性，这限制了该算法在许多实际问题中的应用。文献[22]提出一种基于压缩信号协方差矩阵最大特征值的稀疏度估计方法，但该算法应用的最大特征值具有较大随机性，估计精度有待进一步提高。文献[23]推导了压缩信号协方差矩阵的极限特征值概率密度函数以及能量与稀疏度之间的关系，提出了一种基于压缩信号平均能量的稀疏度估计算法，算法对稀疏度的估计精度高并且计算复杂度较低，但算法实现依赖压缩率以及信噪比等先验信息。

3.2 波达方向(Direction of Arrival,DOA)估计

通过DOA估计，能够获取无线通信系统中目标信号源的位置和角度等信息。在通信干扰抑制研究中，能估计出信号和干扰的来向即可通过控制天线阵列的方向图实现增强信号、削弱干扰的目的。与传统DOA估计方法[24]相比，从稀疏信号重构的角度进行DOA估计具有所需数据样本数量较少，对信噪比(Signal-to-Noise Ratio,SNR)灵敏度较低以及具有处理相干源的能力等优势[25]。

Sacchi等[26]首先提出利用柯西先验约束DOA估计的稀疏性，并采用迭代方法求解优化问题实现DOA估计的算法。文献[27]利用FOCUSS算法及其改进算法得到目标定位系统的稀疏解，实现了信号源DOA的估计，但当SNR较低时，算法性能下降严重。Fuchs提出了基于波束域稀疏重构的信号源DOA估计算法[28]，该算法将波束输出矢量建模为基矩阵列向量的线性组合，利用l1范数约束稀疏向量的稀疏度，l2范数约束背景噪声强度，得到了较好的DOA分辨效果。该算法实现需要较多快拍数，不适用于相关信号的DOA估计。Malioutov等[29]通过利用l1范数约束接收信号的稀疏性，提出了L1-SVD算法，该算法能够得到优于传统方法的DOA分辨能力和估计精度，算法鲁棒性较好并且能同时适用于单测量数据以及多快拍数据。此外，该算法适用于相关信号的DOA估计。但由于算法采用SVD分解方法提取信号子空间，当目标个数估计不准确时会导致信号子空间估计错误，进而降低算法性能。

文献[30]通过结合独立成分分析和稀疏重构的思想，提出了适用于多径信号欠定DOA估计的算法，该算法适用于处理目标个数大于阵元个数的工作场景。Zheng Ling等[31]将短时傅里叶变换和稀疏重构的思想结合起来，提出了基于短时傅里叶变换值稀疏表示的DOA估计算法。该算法能够实现高分辨率的DOA估计，同时该算法也适用于欠定工作场景。Ottersten等[32]通过理论分析证明矢量化样本协方差矩阵与理论协方差矩阵之间存在误差，并且该误差矢量近似服从渐近高斯分布。据此，学者们提出了基于协方差矩阵稀疏重构的DOA估计算法[33]。该算法具有较好的DOA估计精度，但当快拍数较少时算法性能较差。

4 压缩域干扰抑制

压缩域干扰抑制方法始于Davenport等[34]的研究工作，利用干扰和信号压缩分量的正交特性构造滤波算子，提出了一种压缩域滤波算法，可以实现对压缩信号中干扰分量的有效滤除。由于直接对压缩数据进行处理，算法复杂度较低并且实现简单，但该算法要求干扰和信号在同一稀疏字典上得到稀疏表达，算法实现需要获取干扰子空间、干扰稀疏度等先验信息。Chang等[35]对文献[34]中测量矩阵的RIP性质和RIC性质进行了详细的数学推导，给出了算法的RIC上界。Wang等[36]针对文献[34]中滤波算子会对有用信号造成损伤并且无法抑制噪声的不足，提出了基于最小均方误差(Minimization Mean Square Error,MMSE)的压缩域干扰抑制算法，但该算法需要获取干扰稀疏度、系统SNR、系统干信比(Jamming-to-Signal Ratio,JSR)等先验信息，算法应用范围较小。田鹏武等[37]针对文献[34]算法要求干扰和信号满足正交性的不足，提出了基于倾斜投影算子的压缩域滤波算法，进一步扩展了算法的应用范围，但是该算法只是改进了算法中滤波算子的构造方法，针对算法实现依赖较多干扰先验信息的不足没有提出相应的改进方法。Liu等[38]提出了基于稀疏最大似然估计(Maximum Likelihood Estimation,MLE)的压缩域干扰抑制算法，该算法实际上是对文献[34]的进一步发展和完善。裴立业等[39]利用噪声和信号的不同稀疏特性，通过构造测量矩阵实现对信号采样而对噪声不采样，提出了压缩域宽带噪声干扰抑制算法。该算法本质上与文献[34]相同，只是利用预处理方法获取干扰子空间，算法的鲁棒性更好，但算法复杂度较大。

4.1 OFDM通信压缩域干扰抑制方法

在接收端和发送端精确同步的条件下，OFDM系统时域接收信号可以表示为[40]

y=HFzPs+Λf0HJj+n

(6)

式中:H和HJ分别表示发送信号和干扰对应的多径信道增益矩阵；s为OFDM信号；n为背景噪声；j为干扰信号；Λf0为干扰的频率补偿矩阵；FzP表示预编码矩阵。

经过适当变换后，可将式(6)表示为

(7)

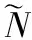
1)针对NBI的抑制方法。文献[40]提出首先进行OFDM系统中的NBI的估计，然后进行时域对消的NBI抑制算法，并把该算法扩展到电力线通信和具有频率偏移的NBI的中继系统。文献[41]进一步将该算法推广到时变衰落信道条件下的NBI抑制。刘思聪等[42]通过利用相邻时域同步OFDM(Time Domain Synchronous OFDM,TDS-OFDM)帧头的差分采样建立压缩采样模型，能够在不依赖信道估计的条件下，精确重构NBI并实现干扰抑制，显著提高了传输系统的鲁棒性。但从导频信号中估计出的NBI与数据符号中的NBI并不完全一致，该算法只适用于TDS-OFDM系统[43]，并不适用于循环前缀OFDM(Cyclic prefix OFDM,CP-OFDM)系统。此外，具有一定带宽的NBI在传统的CS框架下是非稀疏的，传统的CS方法在对具有一定带宽的NBI估计效果较差。文献[44]针对该问题利用循环前缀与其OFDM符号块中的副本之间的差分操作构建NBI稀疏表示模型，然后利用改进的BSBL算法实现NBI的重构，并在时域对消NBI，实现了对具有一定带宽的NBI的有效抑制。

2)针对噪声脉冲干扰的抑制方法。噪声脉冲干扰是一种猝发信号，在时域具有稀疏性。部分学者利用噪声脉冲干扰的这一特性，提出了基于重构对消的压缩域噪声脉冲干扰抑制方法。文献[45]首次提出基于凸优化的压缩域噪声脉冲干扰抑制算法。文献[46]充分利用离散Fourier变换矩阵的结构特性及噪声脉冲干扰幅度分布的先验信息，提出了低复杂度的压缩域噪声脉冲干扰抑制算法。文献[47]采用混合高斯模型对OFDM系统中的突发性噪声脉冲干扰进行建模，基于稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)方法迭代重构噪声脉冲干扰，然后在时域对消噪声脉冲干扰。尽管压缩域噪声脉冲干扰估计和对消方法实现了优于传统方法的干扰抑制性能，但该方法降低了OFDM系统的频谱效率。此外，当背景噪声较强以及噪声脉冲干扰稀疏性较差时，上述方法会导致噪声脉冲干扰估计不准确，进而影响噪声脉冲干扰的抑制效果。文献[48]针对上述问题，提出利用BSBL估计异步噪声脉冲干扰的算法，进一步提高了噪声脉冲干扰抑制算法的鲁棒性。此外，刘思聪等[49]将机器学习的思想引入到OFDM系统中噪声脉冲干扰的抑制，提出了基于稀疏机器学习的OFDM通信压缩域脉冲干扰抑制算法，进一步提高了对噪声脉冲干扰的抑制效果。

4.2 扩谱通信压缩域干扰抑制方法

1)DSSS通信压缩域干扰抑制方法。干扰条件下DSSS系统的接收信号可以表示为

x=s+j+n

(8)

式中，x表示系统接收信号。

文献[50]详细分析了DSSS信号和多音干扰的不同压缩域特性，并利用贪婪算法分别实现干扰稀疏系数向量和信号稀疏系数向量的估计，将压缩域干扰抑制问题建模为式(9)所示的模型：

(9)

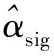
文献[51]将该算法进一步推广到扫频干扰的抑制，利用相同思想实现了DSSS通信中扫频干扰的有效抑制。上述算法虽然能够有效实现对DSSS通信中多音干扰和扫频干扰的抑制，但是算法依赖于干扰稀疏度先验信息。对于信号接收端而言，干扰稀疏度先验信息难以获取。文献[52]针对这一不足，提出了压缩域自适应干扰抑制方法，该算法通过推导贪婪算法迭代中干扰归一化残差的变化，证明经过多次迭代后干扰归一化残差趋近于常数，将该常数作为干扰迭代终止阈值能够实现算法流程的控制，进而实现不依赖于干扰稀疏度先验信息的干扰抑制。算法实现简单，对多音干扰和扫频干扰等具有高度稀疏性的干扰类型具有较好的干扰抑制性能。

文献[50-52]中所提干扰抑制算法均要求干扰在相应的稀疏字典上具有高度稀疏度性，然而将干扰建模为具有一定带宽的NBI更接近于干扰的真实情况。上述算法对具有一定带宽的NBI抑制性能较差。文献[3]针对这一不足，详细分析了DSSS通信NBI的频域块稀疏特性，提出了基于改进BSBL算法的DSSS通信NBI抑制算法。该算法利用DSSS信号的类噪声特性，将干扰估计问题建模为式(10)所示的模型。

y=Φ(s+j+n)=ΦΨNBIαNBI+Φ(s+n)=

ΦΨNBI(αNBI+αs+αn)=ΘNBI(αNBI+αs+αn)

(10)

式中:ΨNBI和αNBI分别表示NBI稀疏字典和稀疏系数向量；αs和αn分别表示发送DSSS信号和噪声系数向量；ΘNBI表示干扰信号感知矩阵。

由于噪声和DSSS信号不能在干扰稀疏字典上得到有效稀疏表示，因此||αs+αn||2相比于||αNBI||2较小，利用改进的BSBL算法能够从压缩信号中重构出NBI，进而在时域对消干扰，实现对DSSS通信中NBI的有效抑制。由于算法利用改进的BSBL算法实现NBI重构，算法运行效率较低。

2)跳频通信(Frequency Hopping Spread Spectrum,FHSS)压缩域干扰抑制方法。针对FHSS通信干扰抑制问题，文献[53]提出了基于自学习的FHSS通信压缩域多音干扰和扫频干扰抑制算法，该方法能够实现对两类干扰的有效抑制，但由于算法在实现中需要不断学习干扰特征，算法复杂度较大。文献[54]将文献[53]中方法拓展到FHSS通信扫频干扰的抑制，实现了对FHSS通信扫频干扰的有效抑制。但由于构建的FHSS信号字典和扫频干扰字典不完全满足形态学成分分析要求，干扰抑制过程中将对信号造成损伤，导致FHSS信号解调性能有所降低。针对FHSS通信中常见的梳状干扰的抑制问题，文献[55]详细分析了梳状干扰的频域块稀疏特性，以及梳状干扰和FHSS信号压缩域的可分性，提出了基于BSBL的FHSS通信压缩域梳状干扰抑制算法，算法能够在梳状干扰覆盖跳频信号多数频点的条件下实现对梳状干扰的有效抑制，进一步提高了FHSS通信梳状干扰抑制能力。但由于使用BSBL算法估计梳状干扰，算法计算效率较低，算法时效性较差。此外，算法只能实现对干扰的抑制，而不能完全消除干扰的影响。

4.3 压缩域干扰抑制方法对比分析

综合分析上述文献中提出的压缩域干扰抑制算法，可分为以下3类。

1)基于线性测量的干扰抑制方法[34,37,39]。该类算法通过设计具有不同特性的测量矩阵实现对接收信号的选择性测量，达到对信号进行压缩采样而对干扰不进行压缩采样的效果，进而实现干扰抑制。该方法由于在线性测量阶段实现干扰抑制，算法结构简单，干扰抑制效果较好。该类方法的不足包括：无法验证选择性测量矩阵的RIP性质；在选择性测量中对受干扰的信号不进行压缩采样，将降低信号的重构性能，进而降低重构信号的解调性能；由于算法实现需要不断寻找最优的干扰子空间，算法计算效率较低。

2)基于干扰、信号分离的干扰抑制方法[50-54]。该类算法直接利用压缩域干扰和信号的可分性实现干扰与信号的分离，进而实现干扰抑制的目的。该类方法的优点是算法计算简单，不需要重构干扰或是只需要部分重构干扰，降低了干扰抑制算法的实现复杂度。该类方法的不足包括：要求干扰具有高度稀疏性，干扰稀疏性较差将降低信号重构性能；对信号和干扰的稀疏字典要求较高，要求分别构建信号和干扰的稀疏字典且信号和干扰在彼此的稀疏字典上不能够得到稀疏表示。

3)基于重构对消的干扰抑制方法[3,40-49,55]。该类算法可以实现有效的干扰抑制，干扰强度越强，干扰重构效果越好，该类方法主要应用于干扰强度较强的条件下，并且由于使用“重构-对消”的干扰抑制策略，该方法可以解决传统干扰抑制方法对信号损伤较大的不足，干扰抑制性能较好。该方法的不足包括：该类算法存在一个悖论，即干扰越强，干扰重构精度越高，但是由于干扰重构精度不能无限提高，在强干扰条件，干扰抑制后仍然会对信号造成干扰，该类算法与传统干扰抑制算法一样存在干扰抑制不彻底的不足；由于需要实现干扰对消，算法硬件实现需要使用多天线结构，增大了算法硬件实现代价。

5 压缩域干扰抑制研究展望

压缩域干扰抑制方法适用于压缩采样后信号的干扰抑制处理，相比于传统的干扰抑制方法，压缩域干扰抑制方法兼顾了大带宽信号处理中降低系统采样率与实现干扰抑制的两大需求，是伴随CS理论和应用研究发展而出现的新的研究方向。总的来看，压缩域干扰抑制研究已经取得了初步的研究成果，但仍然有一些问题需要进一步深入研究。

1)干扰类型分类和识别问题。压缩域干扰检测研究已经取得了部分研究成果，但仍然存在众多需要解决的问题，比如，现在的干扰检测研究中大多假设干扰类型已知或已知干扰在某个稀疏字典上能够得到稀疏表示，而实际中干扰检测的目的之一就是要获取干扰类型，实现干扰识别。因此，已有的干扰检测方法无法满足实际需求。为进一步提高压缩域干扰检测方法的实用性，下一步需要探索利用压缩信号直接进行干扰分类和识别，在该方面的研究中机器学习和深度学习等可能会成为可用的技术手段，文献[49]在这方面进行了初步的探索。

2)干扰参数估计问题。干扰参数估计中需要重点解决的问题即干扰稀疏度信息的获取问题。已有的干扰抑制方法基本上都假设已经获取干扰稀疏度信息或是能够依靠经验设置干扰稀疏度，这与实际情况不符。此外，已有的不依赖于稀疏度先验信息的CS重构算法在存在噪声时，算法性能较差，不适用于压缩域干扰抑制研究。目前，专门开展干扰稀疏度估计的研究成果还未见报道，可行的思路是将信号稀疏度估计方法应用干扰稀疏度估计中，但由于干扰信号特性相比于通信信号特性有差别，并且干扰是时变的，这要求干扰稀疏度估计算法具有更好的时效性和可靠性。此外，干扰参数估计不仅仅局限于干扰稀疏度的估计，更进一步的可以实现对干扰频率和带宽等参数的估计，解决该问题的关键是建立支撑原子位置信息与干扰频率信息之间的关系。文献[10,56]在这方面进行了初步的探索。

3)相干干扰的压缩域抑制问题。相干干扰是通信信号中典型的干扰威胁，而目前的压缩域干扰抑制方法的研究对象都为非相干干扰，已有方法对相干干扰无法实现有效的干扰抑制。这主要是因为相干干扰与通信信号具有相同或相似的压缩域特性，导致干扰与信号在压缩域不可分，无法实现有效的干扰抑制。针对该类干扰的抑制问题，可以通过尝试使用空间谱估计的方法，利用干扰与信号的空域稀疏性以及可分性探索相应的干扰抑制方法，实现对该类干扰的抑制。本文在3.2小节对DOA估计方法的总结概括可以为该问题的研究提供参考。

4)多维域联合干扰抑制问题。在复杂电磁环境下，通信系统面临的干扰威胁类型众多，特性差别较大。此外，在军用通信中，人为恶意干扰功率往往较大，只依靠单一的干扰抑制方法无法实现对干扰的有效抑制。如果能够充分利用干扰和通信信号在不同域的特性，实现多域联合的干扰抑制，则能够充分挖掘各个域干扰抑制方法的能力，有望实现更好的干扰抑制效果，比如联合空间谱估计的压缩域干扰抑制方法等。文中3.2小节对基于稀疏表示的信号DOA估计方法的总结概括可以为研究该问题提供参考。

5)借鉴其他类信号压缩域干扰抑制方法问题。目前，基于压缩域的干扰抑制方法在多种系统的干扰抑制方法研究中都取得一定的研究成果，比如雷达信号干扰抑制处理，数字图像干扰抑制处理等。相比于通信信号的压缩域干扰抑制方法，这些系统中的压缩域干扰抑制方法的实现途径和研究思路都有不同程度的差别。充分借鉴这些系统中的压缩域干扰抑制方法可以进一步拓宽通信信号压缩域干扰抑制方法的思路，为进一步提高通信信号压缩域干扰抑制方法的性能提供新的可能性。

6 结束语

本文对典型大带宽通信的压缩域干扰抑制方法进行了系统的梳理，详细分析了大带宽通信信号干扰抑制需要解决的压缩域干扰检测、压缩域干扰参数估计和压缩域干扰抑制三个方面问题的研究进展和现状。对已有算法的性能进行了分析和评价，指出了已有算法的优势和不足，对未来的研究方向进行了展望，为深入开展压缩域干扰抑制研究提供了有意义的参考。