疲劳和刚度失效模式下矿井提升机主轴系统的可靠性研究

王海峰,王新刚,胡福豪

(东北大学 机械动力学与可靠性研究中心，河北 秦皇岛 066004)

主轴系统作为矿井提升机的关键组成及承载部分，其工作状态的稳定性和可靠性直接影响整个提升机系统的可靠性[1]。主轴系统长期受到随机交变载荷的作用，各个零件内部损伤逐渐积聚扩展，材料的各种物理属性如初始强度也出现逐渐退化的趋势[2]。另一方面，由于主轴系统受载状态复杂和工作环境较为恶劣，且各功能部件的动力传递互相影响，且多种失效模式耦合在一起，分析较为困难。传统的基于静强度理论的可靠性方法不能很好的反映出主轴系统在性能退化下的各种失效模式耦合作用对主轴系统及整机可靠性的影响，因此很难准确估计出提升机的使用寿命。Song和Kang[3]通过矩阵的代数运算描述了机械系统中的失效相关性，同时采用相关系数矩阵法对研究对象进行可靠性预估。Zhang等[4]采用最大熵法、随机摄动法等，对多自由度系统中存在的单一相关失效模式的可靠性进行了研究和分析。Yu等[5]以冗余系统为研究对象，通过“相关性函数”建模来描述其各个失效模式之间的相关性。Schottl[6]在总结前人研究成果的基础上，提出了基于失效相关的系统可靠性数学模型，此模型的应用范围更为广泛，它不仅可以用于分析共因失效，还能用于描述多种不同原因造成的失效。Sun等[7]通过建立失效相关的可靠性数学模型对零件的失效相关程度进行了量化描述。上述文献方法仅考虑了失效模式之间相关性的数学建模和对可靠性的影响，没有考虑产品性能退化及相关系数变化对模型建立和精度的影响。

本文从强度退化和失效模式相关性两个角度的出发，借助Gamma过程和混合Copula理论建立提升机主轴系统的可靠性数学模型，并采用Monte Carlo method法对考虑多种失效模式下矿井提升机主轴系统及其零件的可靠性进行仿真分析，给出主轴系统的可靠度变化趋势，为实际工程中准确评估提升机的整机性能和剩余寿命提供理论支撑。

1 主轴系统的力学分析

1.1 主轴系统的基本结构及提升周期

矿井提升机主轴系统结构如图1所示，包括主轴、游动卷筒、固定卷筒、轮毂等附属零件。

提升机在作业时，整个主轴的受力情况较为复杂，直径不同的主轴截面受力情况也不同，很难直接去计算整个主轴在各种工况时的受载情况。本文总结了以往的研究成果，首先确定出其危险截面，即固定卷筒左支轮所在的截面[8-9]，其次，按照表1所示6种工况对主轴进行受力分析，模拟出危险截面在各种工况下的力学模型，并按此模型进行后续主轴可靠度的分。

表1 工况表

根据主轴转速和卷筒有效宽度(钢丝绳的有效缠绕宽度)，可求出每种工况的作业时间t，6种工况组成一个完整的周期，时间为7.2 min。

t=t1=t2=t3=t4=t5=t6=

(1)

1.2 系统主要部件的力学分析

表2为主轴系统各零部件物理参数。

表2 主轴系统各零部件物理参数

续表(表2)

为分析计算方便，在主轴的各轴段选择5个截面，受力简图如图2。

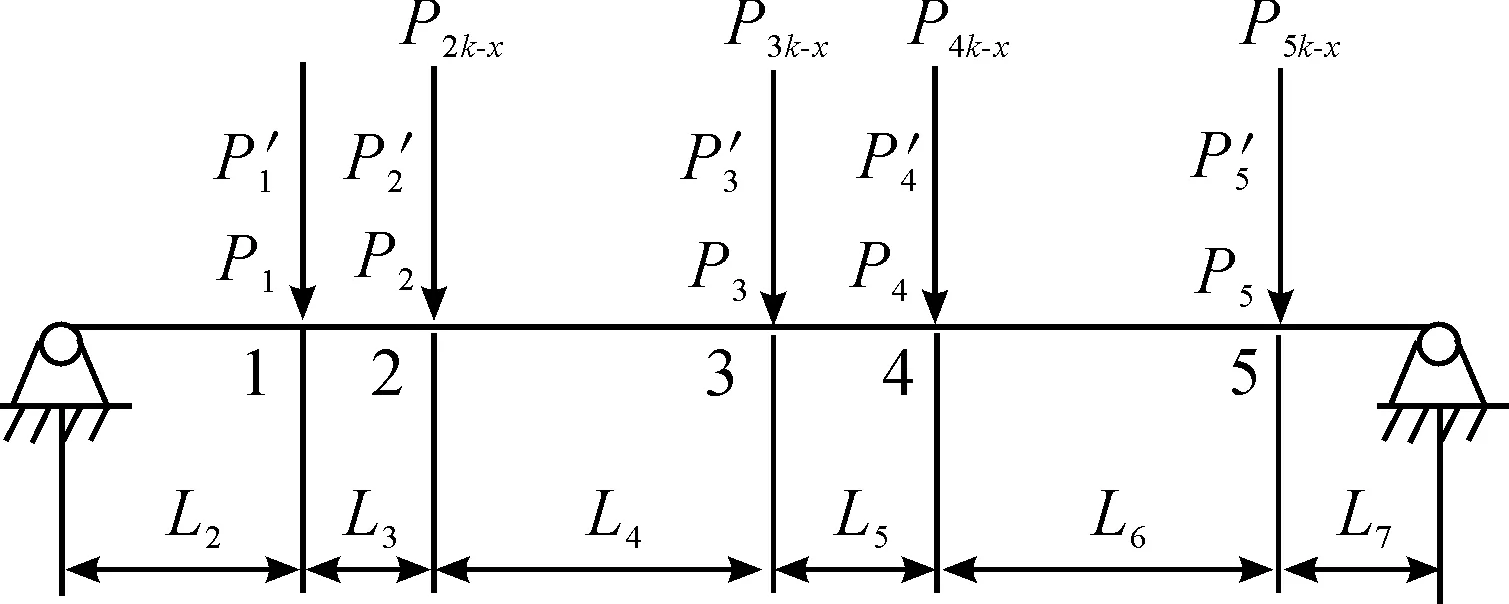
图2 矿井提升机主轴受力简图

图中，Pi为各截面处的主轴重力，Pi′为各截面处的零件重力，Pik-x为各截面处的钢丝绳重力。其中，i=1,2,3,4,5分别对应五个截面，x=1,2,3,4,5,6分别对应六种工况。在考虑主轴重力、钢丝绳重力、附属件重力下的各截面处的载荷如式(2)所示：

(2)

已知危险截面处直径、抗弯截面系数和抗扭截面系数，

得出危险截面截面4处的弯曲应力、扭转剪切应力如式(3)所示：

(3)

由式(3)可得，疲劳强度失效模式下主轴的功能函数：

(4)

其合成应力S的表达式如式(5)所示，主轴和卷筒危险截面的受力分析及推导过程见文献[10]。

(5)

综合分析主轴及卷筒所受到的重力和绳拉力得出危险截面的合成应力变化分别如图3和图4所示。

图3 主轴危险截面合成应力

图4 卷筒危险处合成应力

2 各零件的强度退化模型

本文用Gamma过程来描述材料的强度退化规律，从材料的疲劳试验数据着手，利用Matlab模拟出P-S-N函数式，并对Gamma过程中的形状参数v(t)及退化尺度参数u进行估计，得出材料的强度退化数学模型。

主轴材料为45号钢，利用Matlab对采集的45号钢的疲劳实验数据进行曲线模拟，如图5所示。

已知提升机主轴额定转速为40 r/min，取时间单位为h，主轴受载次数N与时间t存在如下关系：N=f(t)=40×60t=2 400t。将不同存活率下S-N曲线转化为相应S-t曲线，得出45号钢在4种不同存活率下S-t曲线的显示表达式如表3所示。

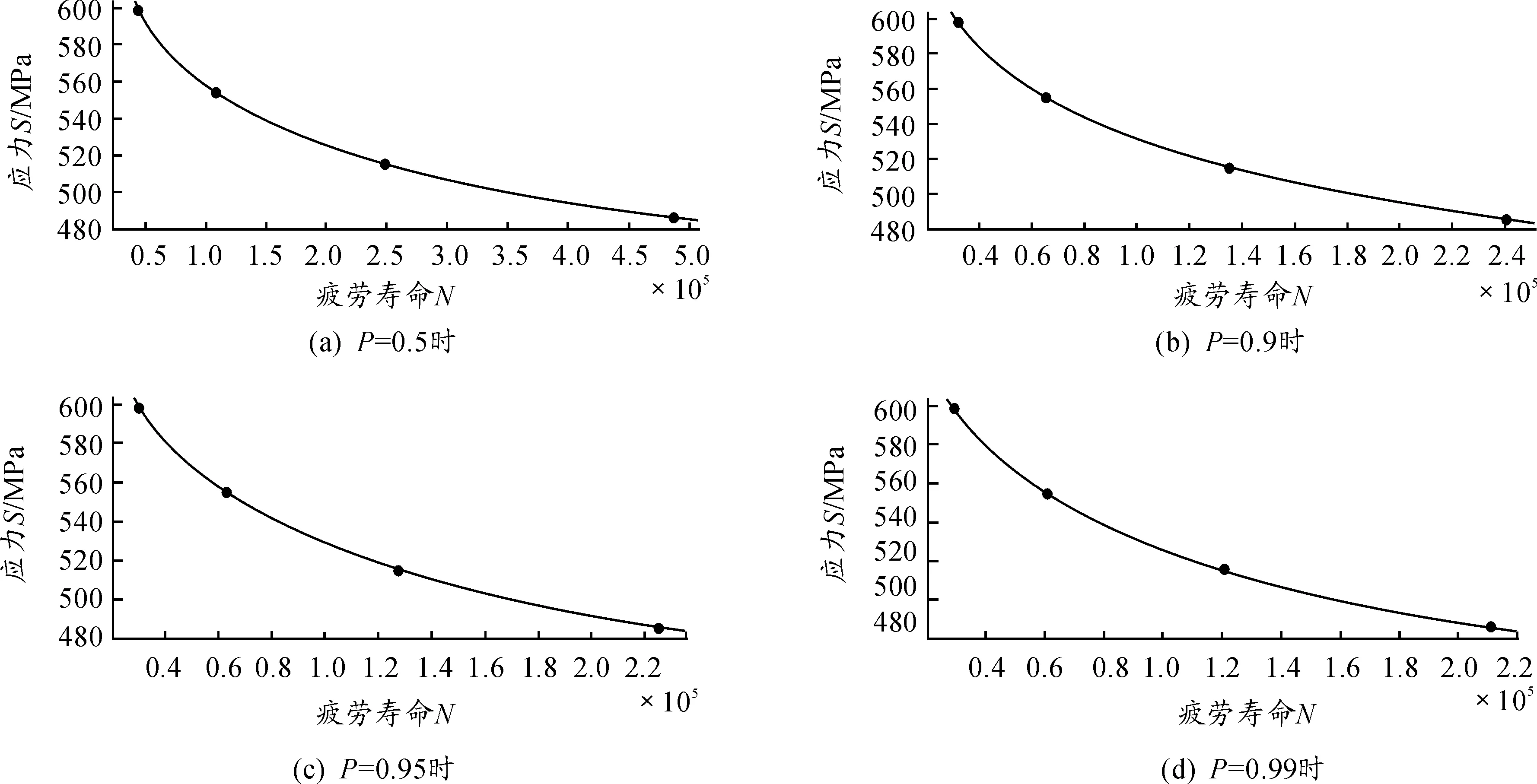
图5 主轴材料的P-S-N曲线

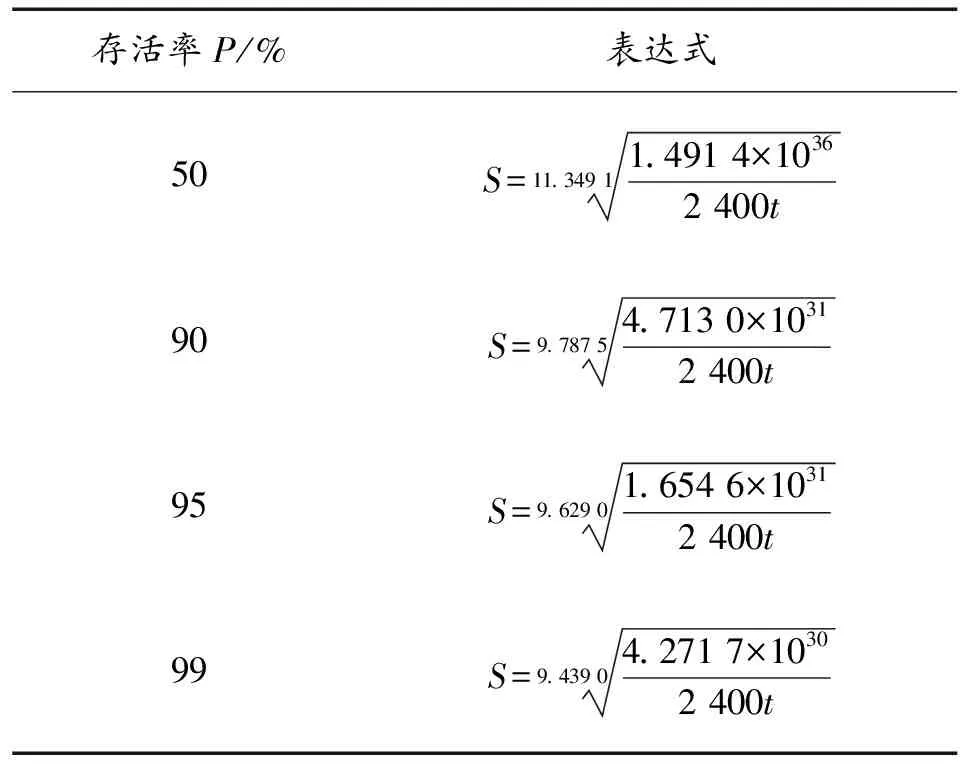
表3 P-S-t曲线显示表达式

取时间段[t1,t2]=[2 500,5 000]h，根据P-S-t曲线可得强度退化量估计值ΔDm1如表4所示，均值何方差如式(6)所示。

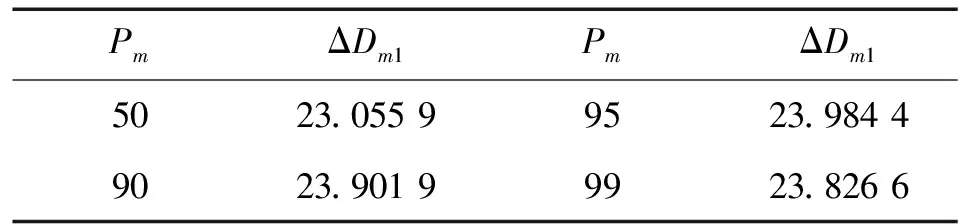
表4 强度退化量的估计值

(6)

Gamma过程中的形状参数v(t)及退化尺度参数u的估计值如下：

(7)

取步长为tn=n×2 500小时，则tn+1=(n+1)×2 500。当n=1～9时，求所有时间区间[tn+1,tn]对应的un和an的值，如表5所示。

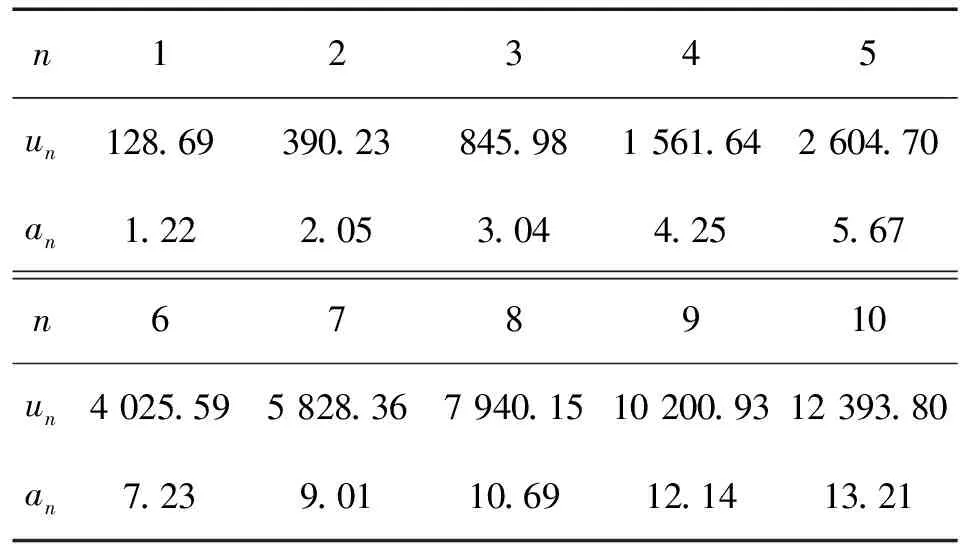
表5 Gamma参数估计值

主轴Gamma退化过程特征参数的估计值分别为：

(8)

因此，主轴的强度退化服从形状参数为v(t)=6.853 3t，尺度参数为u=4.592 0×103的Gamma过程。主轴材料的强度退化规律如图6所示。

同理可得，卷筒材料的强度退化规律如图7所示。

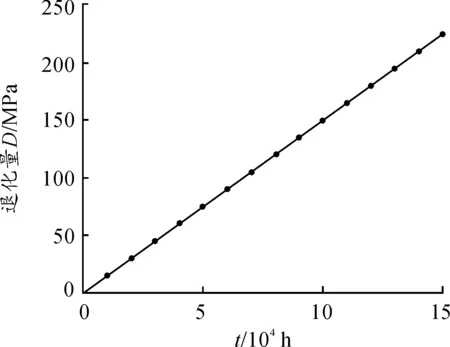
图6 主轴材料的强度退化趋势

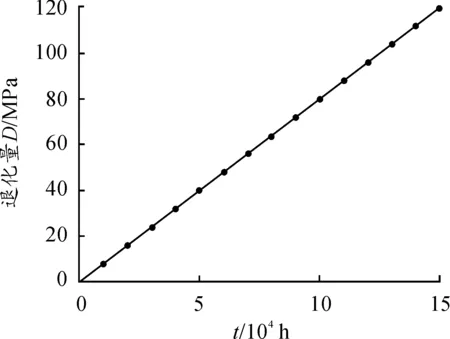
图7 卷筒材料的强度退化趋势

3 主轴系统的可靠性分析

3.1 主轴的动态可靠度分析

主轴在长期交变载荷作用下，其强度会逐渐降低。因此，主轴在疲劳强度失效模式下的可靠度模型是随时间变化的动态模型[11]：

(9)

式(9)中各参数值如表6所示。

表6 主轴疲劳失效模型参数值

采用蒙特卡洛抽样法，对模型中的各部分参数分别抽样75 000次，可得到主轴在疲劳强度失效模式下的动态可靠度曲线，如图8。

图8 疲劳强度失效模式下主轴的动态可靠度曲线

同理，主轴在刚度失效模式下的可靠度模型也是随时间变化的动态模型：

(10)

式(10)中各参数值如表7所示。

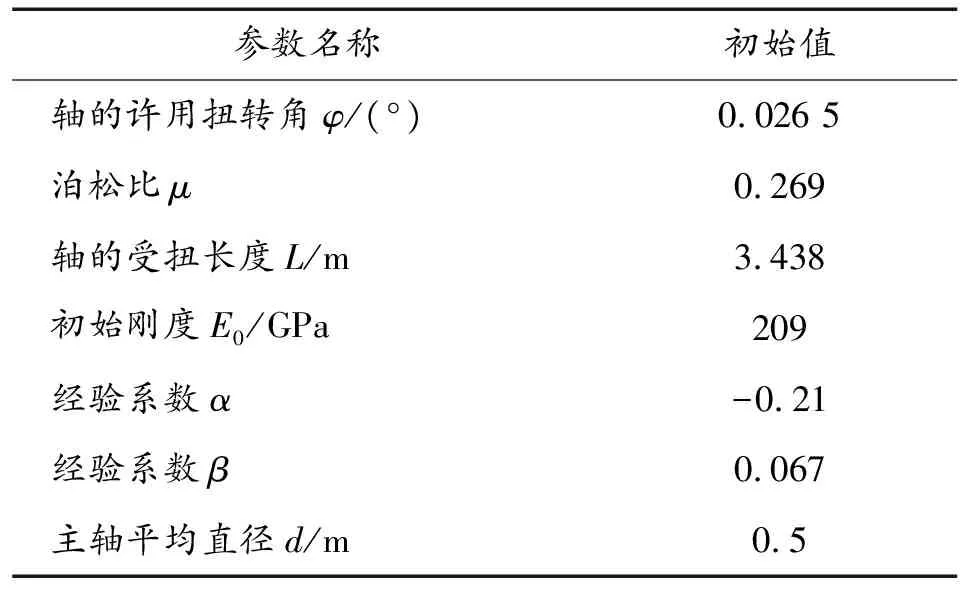
表7 主轴刚度失效模型参数值

主轴在刚度失效模式下动态可靠度曲线如图9。

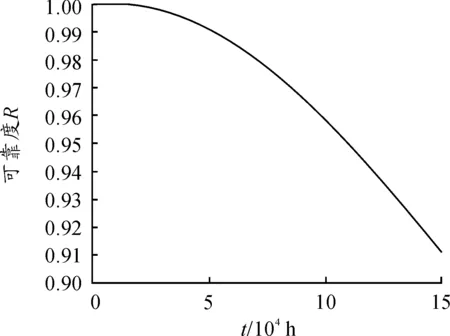
图9 刚度失效模式下主轴的动态可靠度曲线

3.2 卷筒的动态可靠度分析

疲劳强度失效模式下卷筒的可靠度模型为：

(11)

式(11)中各参数值如表8所示。

表8 卷筒疲劳失效模型参数值

卷筒在疲劳强度失效模式下的动态可靠度曲线如图10。

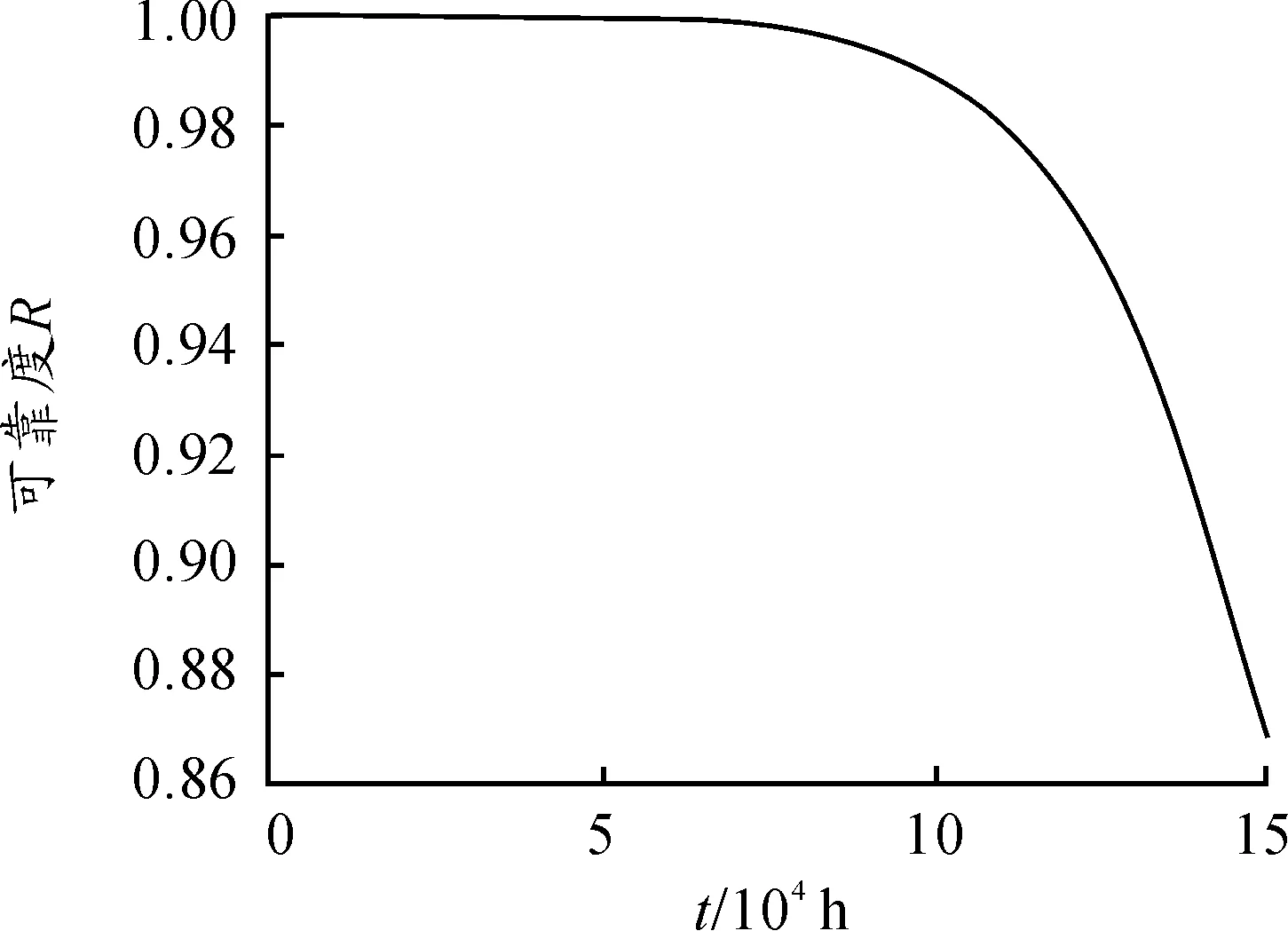
图10 疲劳强度失效模式下卷筒的动态可靠度曲线

卷筒在刚度失效模式下的可靠度模型是随时间变化的动态模型：

(12)

模型中各参数值如表9所示。

表9 卷筒刚度失效模型参数值

卷筒在刚度失效模式下动态可靠度曲线如图11。

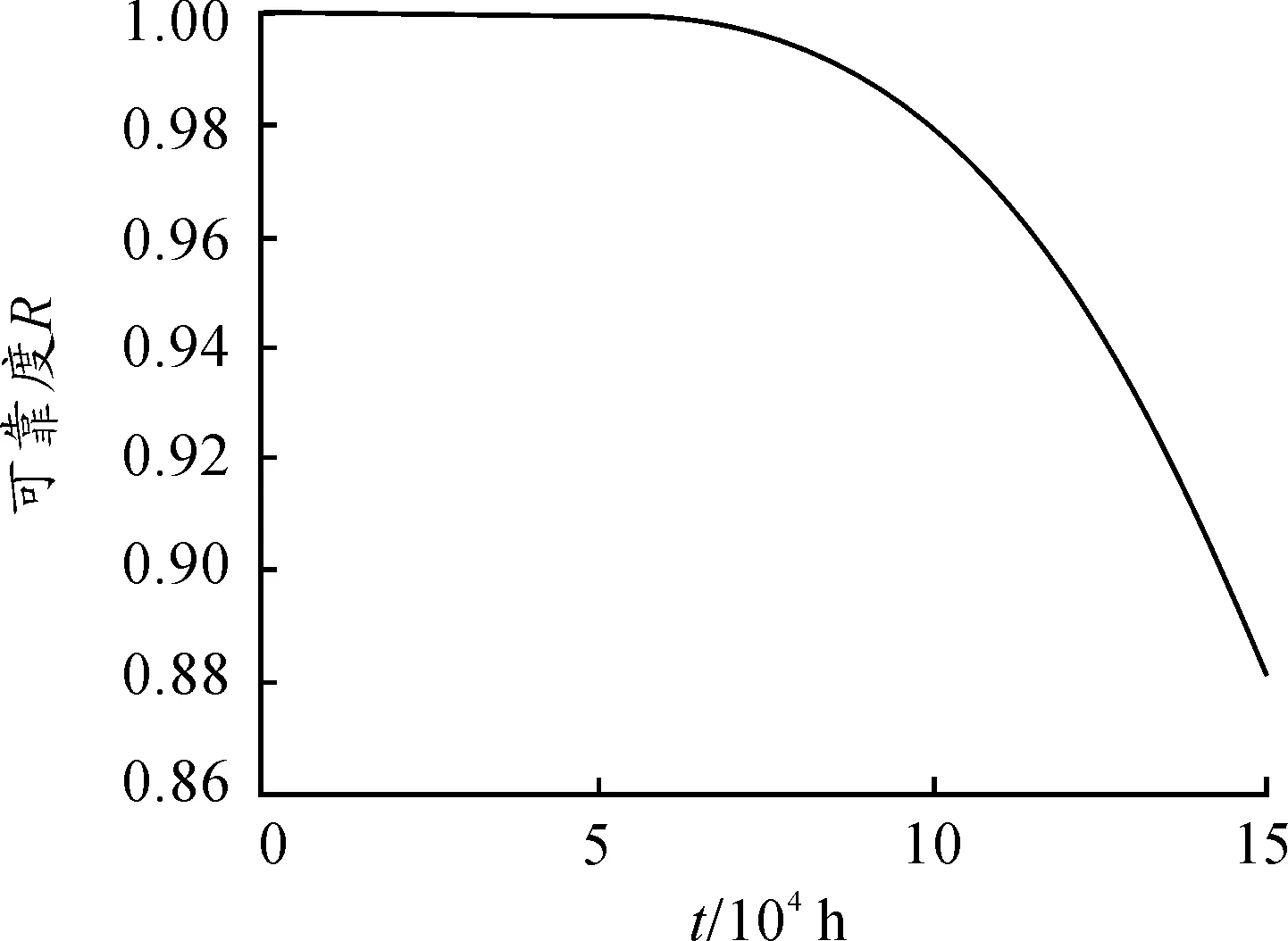
图11 刚度失效模式下卷筒的动态可靠度曲线

3.3 失效模式相关下的各零件可靠性分析

主轴在两种失效模式下的功能函数分别为：

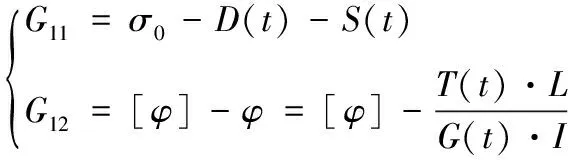
(13)

本文采用混合Copula函数C1(·)来描述G11与G12之间的相关性[12]，如式(14)所示。式中：CG、CC和CF分别为Gumbel、Clayton和Frank Copula函数；α，θ，λ分别为其对应的未知参数；wi(i=1,2,3)为加权系数，且w1+w2+w3=1。其中，相关参数α，θ，λ可以对变量之间的相关程度做定量描述，加权系数w1，w2，w3可以表示变量之间相关模式。

C1(·)=C(u,ν)=w1·CG[u,ν;α]+

w2·CC[u,ν;θ]+w3·CF[u,ν;λ]=

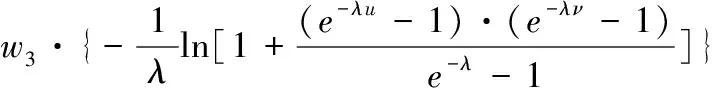
(14)

根据平方和最小法对C1(·)中的6个参数进行计算，DSS取得最小值时所对应的参数结果即为最优解：

(15)

通过fmincon函数求解模型中的各未知参数：

(16)

参数估计结果如表10所示。

表10 混合Copula函数参数估计结果

主轴在疲劳强度失效模式下的可靠度R1，在刚度失效模式下的可靠度R2，令P1n(n=1,2)为主轴在第n种失效模式下的失效概率，λ1为主轴在失效相关时总失效概率，则主轴在失效相关情况下的动态可靠度模型[13]如式(17)所示。

R12=1-λ1=1-Pr(G11≤0∪G12≤0)=

1-{Pr(G11≤0)+Pr(G12≤0)-

Pr(G11≤0∩G12≤0)}=

1-{P11+P12-C1(P11,P12)}

(17)

由上式可知主轴在疲劳强度失效和刚度失效相关情况下的可靠度如图12所示。

图12 失效相关下的主轴可靠度

同理可得，用于描述卷筒中失效相关的混合Copula函数参数估计结果如表11所示。

表11 混合Copula函数参数估计结果

则卷筒在疲劳强度失效和刚度失效相关情况下的动态可靠度如图13所示。

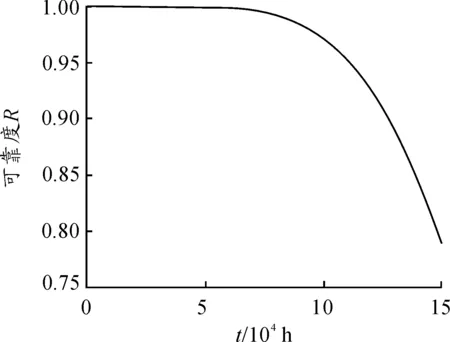
图13 失效相关下的卷筒可靠度

3.4 失效相关下主轴系统的动态可靠度

借助四维混合Copula函数描述主轴系统中各个零件之间的失效相关性，所构建的四维混合Copula模型结构如图14所示。

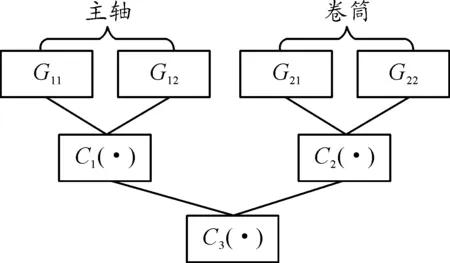
图14 四维混合Copula模型结构简图

疲劳强度失效模式和刚度失效模式下主轴和卷筒对应的功能函数分别记为G11、G12、G21和G22，建立四维混合Copula函数C3(·)来描述G11、G12、G21和G22四个功能函数之间的关联性。

C3(·)=C(u,ν,y,z)=w1·CG[u,ν,y,z;α]+

w2·CC[u,ν,y,z;θ]+w3·CF[u,ν,y,z;λ]=

(18)

四维混合Copula函数参数估计结果如表12所示。

表12 混合Copula函数参数估计结果

主轴系统在失效相关情况下的可靠度如图15所示。

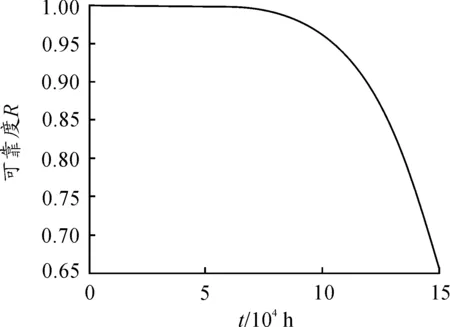
图15 失效相关下的主轴系统可靠度

根据失效相互独立可靠性假设理论，单一零件的可靠度等于各失效模式下的可靠度之积，同时整个系统的可靠度等于各组成零件在各失效模式下的可靠度之积[14]。根据失效完全相关可靠性假设理论，单一零件或系统的可靠度等于各失效模式中的最薄弱环节的可靠度。主轴、卷筒及系统在相互独立、失效相关、完全相关3种情况下的可靠度曲线分别如图16～18所示。

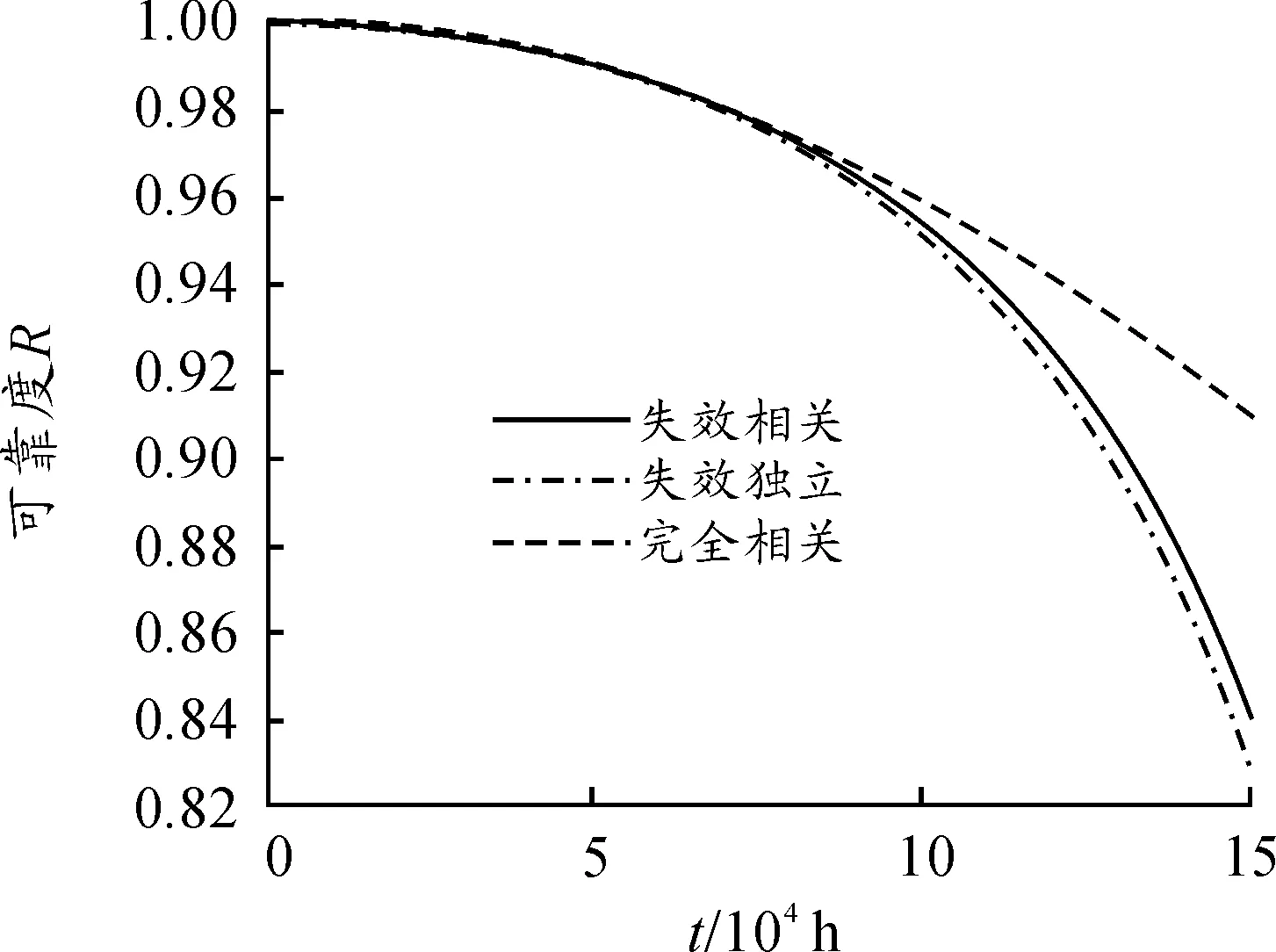
图16 主轴可靠度

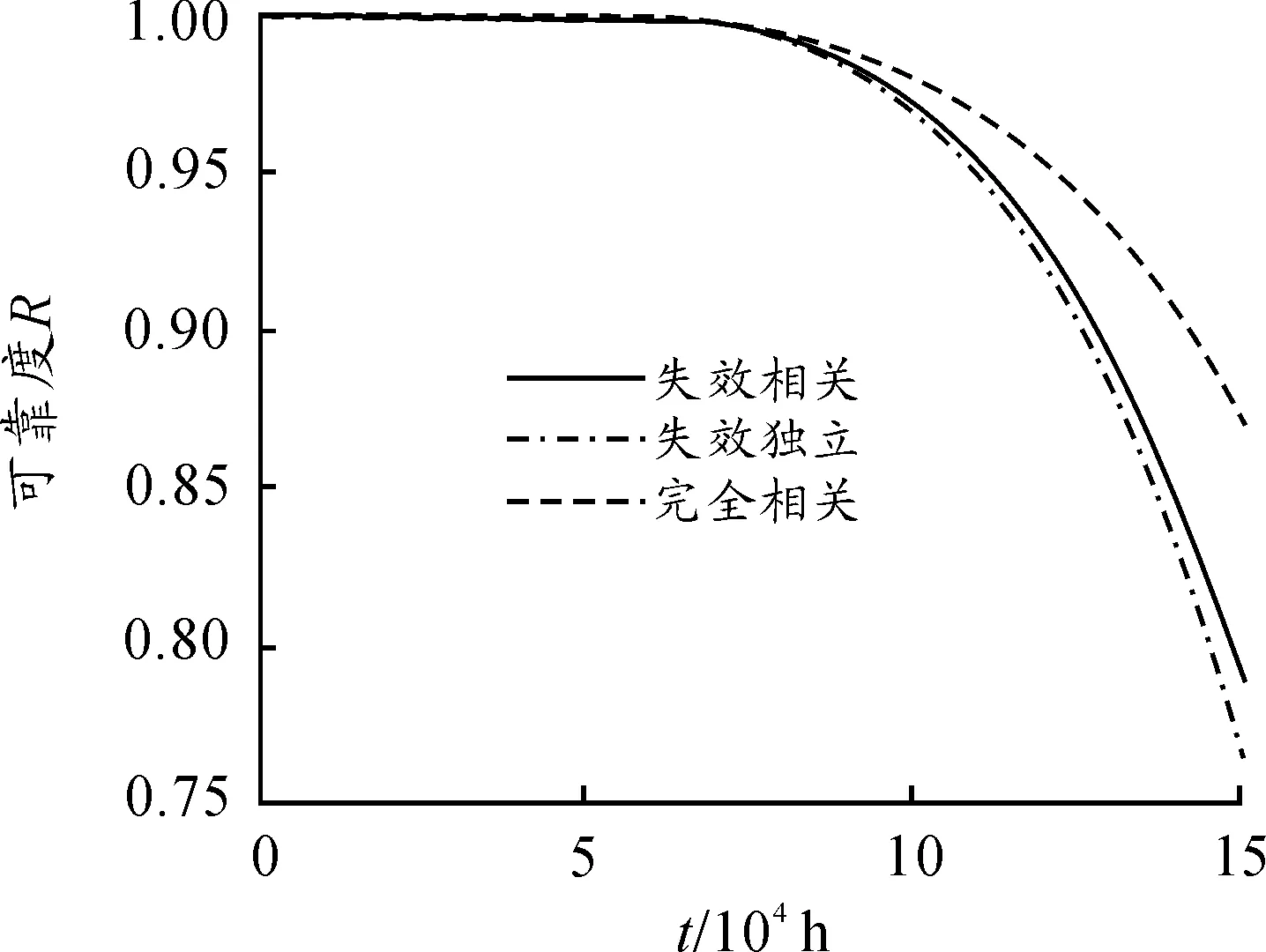
图17 卷筒可靠度

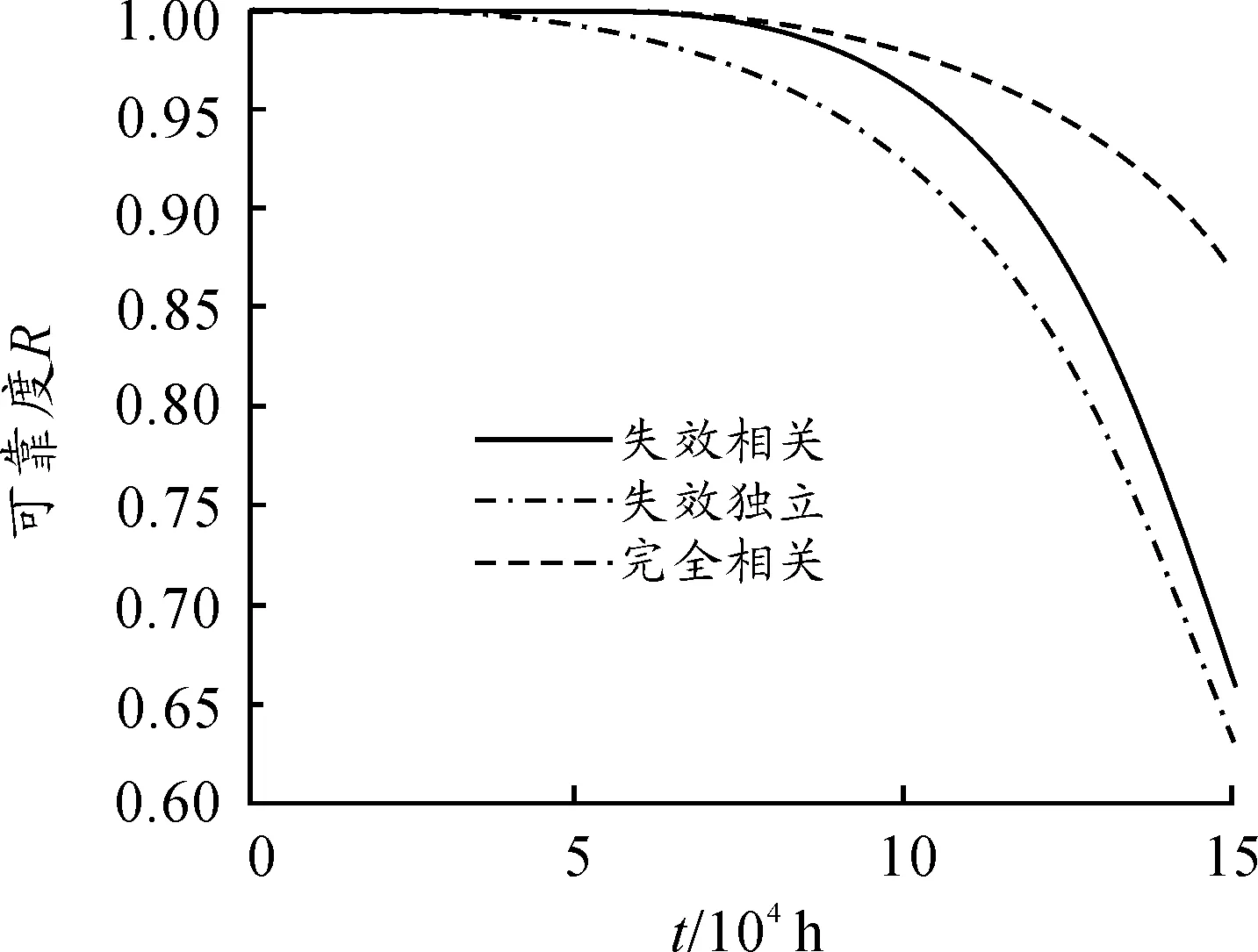
图18 主轴系统可靠度

由以上三图可知，零件或系统在3种情况下的可靠度均随着提升机工作年限的增加逐渐降低，并且在任一时间节点满足R完全相关>R失效相关>R相互独立，即本文基于Copula理论计算出来的零部件和系统可靠度数值在失效相互独立假设理论计算值和完全相关假设理论计算值之间。基于完全相关假设理论对主轴系统的可靠性评估偏高，提升机在作业中可能发生危险；基于失效相互独立假设理论对主轴系统的可靠性评估偏低，过于保守浪费资源。根据现有提升机主轴系统设计参数和故障数据来看，基于混合Copula函数对主轴系统的可靠性评估符合实际情况。

4 结论

1)用Gamma过程来描述主轴系统中零件强度退化规律，能够满足强度退化具有随机性和不可逆性的特征。利用混合Copula函数进行零件和系统的失效相关性建模，能够准确描述整个主轴系统在失效相关情况下的动态可靠度变化规律。

2)该模型既能在设计初期对矿井提升机主轴系统的可靠性进行评估，又可以在服役期对矿井提升机主轴系统的剩余寿命进行估计。

3)本文提出的模型能够灵活准确地描述主轴系统中的各种失效模式之间的关联性，为多失效模式下提升机主轴系统及其他机械系统提供了一种有效的可靠性分析方法。