超音速反舰导弹末端有损飞行弹道分析

张龙杰,胡 慧,张龙云

(1.海军航空大学,山东 烟台 264000; 2.山东大学 岩土与结构工程研究中心, 济南 250061)

反舰导弹末端突防过程中，受到防御系统拦截后，出现的典型毁伤模式有3种[1]：解体、哑弹以及偏航。在弹体受损偏航的情况下，由于毁伤部位和毁伤程度的不同，导弹的飞行弹道会随机多变。在不同飞行速度以及弹目距离下，导弹的飞行轨迹不同，对目标的脱靶量也不同，因此在分析导弹末端可能的杀伤区域以及舰载近程武器系统(CIWS)反导靶场实验的安全性评估过程中，都必须深入分析反舰导弹损伤情况下飞行弹道以及对应的目标脱靶量。

围绕导弹损伤后的运动问题，国内外学者从不同角度进行了研究。文献[2]从反舰导弹实弹射击训练时，对航区内被保护设施威胁概率的求解需求出发，通过概率分析法建立了反舰导弹故障飞行落入概率计算模型，并进行了仿真计算。文献[3]从导弹武器设备子系统和分部件的可靠性和重要性出发，从初始发射异常、发动机故障、姿态控制系统故障等角度，通过仿真分析建立了导弹的典型故障弹道，研究成果对导弹靶场试验的安全控制工作具有积极的推动作用。文献[4]从舵机的角度分析了X型舵故障对导弹控制性能及命中点散布的影响，仿真结果指出，在一些极端初始条件下，舵机故障会使弹道畸变，导致导弹坠落。

本文从系统控制的角度出发，利用一阶和二阶控制环节对导引头和弹体自动驾驶仪的动力学特性进行模拟，在三维广义比例导引(TPN)攻击模型的基础上，对于导弹突防过程中出现的各种损伤模式，将其产生的影响映射到末制导控制回路中，通过对TNP攻击模型的仿真分析，对导弹在不同损伤模式下的飞行弹道进行研究。

1 坐标系

地面坐标系为固定坐标系，原点O位于末制导攻击时刻导弹质心在地面的投影点位置，x0轴指向东向，y0轴指向北向，z0轴指向天向。

平移坐标系的坐标原点M位于导弹的质心点位置，随导弹运动而平动，其余各轴与地面坐标系Ox0y0z0对应的各坐标轴保持平行，如图1所示。

图1中，T为目标，vt为目标速度矢量，vm为导弹速度矢量，vr为相对速度矢量，R为弹目视线矢量。

相对运动坐标系的坐标原点M位于导弹的质心点位置，yr轴始终指向目标T，即与视线矢量R保持一致，zr在视线转移平面MTN内，垂直于yr轴，沿相对速度vr方向为正，xr通过右手定则确定，如图1所示。

图1 导弹三维运动示意图

准弹体坐标系的原点位于导弹的质心点M，xb轴沿导弹纵轴指向弹体头部，zb轴位于铅垂面内指向上方，yb轴通过右手定则确定，如图2所示。

舵机坐标系与导弹固连，原点位于导弹纵轴与舵机控制面的交点Mc上，xc轴与准弹体坐标系的xb轴重合，弹体无滚转情况下，沿xb轴观察，yc轴由原点Mc指向右上角区域的舵面，zc轴由原点Mc指向右下角区域的舵面，并与xc和yc轴构成右手坐标系，如图2。

图2 舵机和准弹体坐标系

2 考虑弹体动力学环节的末制导方程

2.1 导引方程

将国际上通用的TPN导引律[5-7]扩展到三维空间中，采用矢量法在相对运动坐标系Mxryrzr下建立导弹的末制导方程，如图3。

图3 相对运动坐标系

(1)

式(1)中，K为TPN比例系数。ac施加在垂直于R的方向，与vn方向相同，结合图3，根据矢量叉积运算的方向定义,有:

(2)

将式(1)代入式(2)中，得到:

ac=Kvc×ωq

(3)

下面求解vc和ωq。根据矢量点积运算的投影性质，相对速度矢量vr在R上投影速度的大小为:

(4)

由于vc与R方向相反，因此有：

vc/|vc|=-R/|R|

结合式(4)得到法向相对速度矢量vc的求解表达式为：

将上式代入式(3)中，得到：

(5)

对于质量为mt的目标T，其相对导弹M转动的角动量矢量L为：

L=Jtxωq=mt|R|2ωq

(6)

式(6)中，Jtx=mt|R|2为目标T绕xr轴的转动惯量。可以看出，角动量矢量L的方向与视线转动角速度矢量ωq的方向相同。

根据质点角动量的定义，当质点与轴线的距离为R并且绕轴线作圆周运动时，它的角动量L是R与质点的线性动量P的矢量积，即：

L=R×P=R×(mtvr)=mtR×vr

(7)

结合式(6)和式(7)，得到视线转移角速度矢量

ωq=(R×vr)/|R|2

(8)

将式(8)代入式(5)中，得到导引加速度矢量方程为：

(9)

式(9)即为三维空间中的TPN方程。

2.2 控制环节

(10)

式(10)中，Tk为导引头时间延迟常数。一阶控制环节对应的控制结构示意图如图4。

图4 一阶导引头环节

由图4得到求解一阶控制环节的微分方程为：

(11)

对于弹体自动驾驶仪，简化情况下，一般采用一阶控制环节[9-11]进行分析，由于弹体自动驾驶仪往往呈现出高阶动态特性[12]，为了准确模拟导引指令加速度ac与弹体实际输出加速度am的关系，本文以二阶控制环节对弹体自动驾驶仪的高阶动态特性进行模拟，对应的标准传递函数为：

(12)

式(12)中，ζ为弹体阻尼比；ω为弹体无阻尼振荡频率。二阶控制环节对应的控制结构示意图如图5。

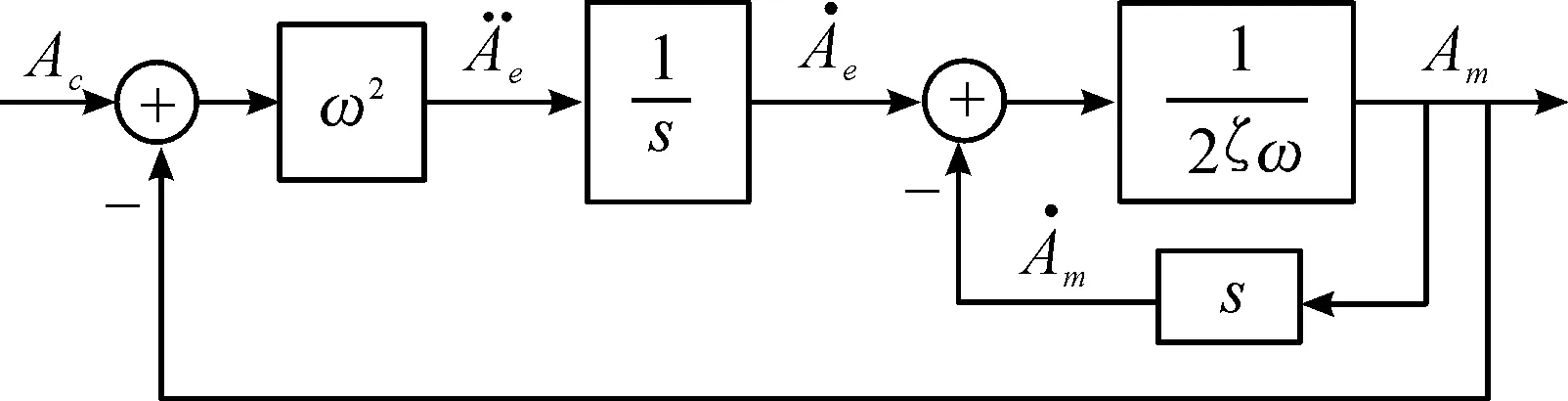
图5 二阶自动驾驶仪环节

由图5得到求解二阶控制环节的微分方程为：

(13)

假设地面坐标系Ox0y0z0下导弹和目标的速度和位置矢量分别为vm,vt以及Rm,Rt，则有vr=vt-vm，R=Rt-Rm，再结合式(5)和式(8)～(13)，得到考虑导引头和弹体自动驾驶仪动态特性的TPN末制导方程为：

(14)

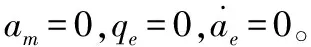
3 故障模式及处理

3.1 故障分类

导弹被CIWS弹丸击中后，会出现多种故障，表1给出了导弹末端突防过程中的几类典型故障及对应的部件。

表1 导弹制导与控制系统故障模式

在对各类故障模式进行分析时，假设导弹不具有故障自修复能力，或者对于具有容错控制[13]的导弹，所有故障都超出了其容错控制的范围。

由式(14)计算得到的am=[a0xa0ya0z]，是地面坐标系Ox0y0z0下的矢量，在准弹体坐标系Mxbybzb下的表示为：

abm=[aeaϑaψ]=amMb0=

(15)

式(15)中，Mb0为地面坐标系Ox0y0z0到准弹体坐标系Mxbybzb的转换矩阵；ae为导弹沿弹体纵轴方向的加速度，主要由发动机推力提供；aϑ,aψ主要由舵面偏转产生。

下面分别对故障模式下3个方向的加速度大小进行分析。

3.2 故障处理

3.2.1控制舵故障

导弹采用“×”型正交舵，图6为从弹体尾部观察“×”型正交舵的布局示意图。

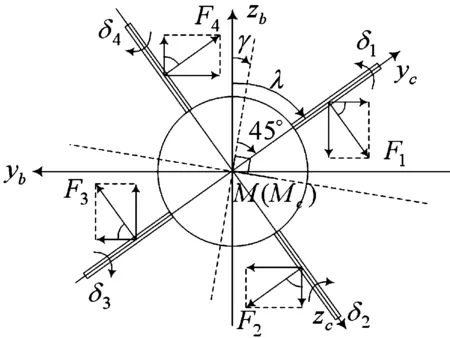
图6 “×”型正交舵示意图

图6中，导弹滚转角γ为零时，从右上角顺时针开始，各舵面依次编号1～4，对应的舵偏角为δ1～δ4，并规定使导弹右偏、低头和右滚转的舵偏角为正。

下面推导“×”型正交舵偏转过程中，在准弹体坐标系Mxbybzb下对应的等效舵偏角。如图6所示，对于“×”型正交舵，各舵面偏转过程中，在准弹体坐标系的yb轴和zb轴方向的合力大小分别为：

Fby=-F1cosλ+F2sinλ+F3cosλ-F4sinλ

Fbz=-F1sinλ-F2cosλ+F3sinλ+F4cosλ

(16)

式(16)中，λ=γ+π/4为各个舵面与准弹体坐标系的zb轴所成的角，λ∈[0°,360°]，顺时针转动为正；Fi(i=1,2,3,4)为舵面偏转引起的空气动力分量，是对应的舵偏角δi的函数，又记作Fi(δi)。对于确定的舵结构，假设各舵面面积相等，有：

Fi(δi)=Kδδi

(17)

式(17)中，Kδ为单位舵偏角产生的空气动力在Mcyczc平面上的投影大小。从而式(16)转化为：

Fby=Kδ(-δ1cosλ+δ2sinλ+δ3cosλ-δ4sinλ)

Fbz=Kδ(-δ1sinλ-δ2cosλ+δ3sinλ+δ4cosλ)

(18)

对应的滚转力矩为：

(19)

式(18)、式(19)中，L为横滚力臂。假设“×”型正交舵的等效俯仰、偏航以及滚转舵偏角分别为δϑ、δψ和δγ，即有Fby=Kδδϑ，Fbz=Kδδψ以及Mγ=KδLδγ/2，结合式(18)、式(19)得：

δϑ=-(δ1-δ3)cosλ+(δ2-δ4)sinλ

δψ=-(δ1-δ3)sinλ-(δ2-δ4)cosλ

δγ=δ1+δ2+δ3+δ4

(20)

式(20)即为“×”型正交舵到等效舵偏角的转换模型。

下面分析等效舵偏角到“×”型正交舵各舵面的分解方法，为此定义δd=δ1+δ3，结合式(20)得到

δ1=(-δϑcosλ-δψsinλ+δd)/2

δ2=[δϑsinλ-δψcosλ+(δγ-δd)]/2

δ3=(δϑcosλ+δψsinλ+δd)/2

δ4=[-δϑsinλ+δψcosλ+(δγ-δd)]/2

(21)

式(21)的解不唯一，这是由于对于“×”型正交舵同样的舵效会存在多种操舵方式，式(22)给出的是一种工程解决方案：

(22)

式(22)中，δf=|δ1-δ3|-|δ2-δ4|。舵面偏转后，最终将改变导弹在不同方向的机动能力。假设舵偏角大小与对应的加速度近似成线性关系，在舵机坐标系Mcxcyczc下，由舵偏角δi(i=1,2,3,4)引起的导弹加速度aci以及绕弹体滚动的角速度大小ωi分别为：

aci=kaδi,ωi=kωδi

(23)

式(23)中，ka,kω为常系数。在舵机坐标系Mcxcyczc下，对于单个控制舵，由于舵偏角最大时对应的加速度值以及滚转角速度值分别达到最大值amax和ωmax，因此式(19)转化为：

aci=kaδi,ωt=ktkaδi

(24)

式(24)中，系数kt=ωmax/amax。定义ωd=kt(ac1+ac3)，再参考式(21)，得到舵机坐标系Mcxcyczc下各舵面产生的加速度的大小为：

ac1=(-aϑcosλ-aψsinλ+ωd/kt)/2

ac2=[aϑsinλ-aψcosλ+(ωm-ωd)/kt]/2

ac3=(aϑcosλ+aψsinλ+ωd/kt)/2

ac4=[-aϑsinλ+aψcosλ+(ωm-ωd)/kt]/2

(25)

式(25)中，ωm=kt(a1+a2+a3+a4)为等效滚转角速度。对于ωd，根据式(22)，有：

(26)

式(26)中，af=|ac1-ac3|-|ac2-ac4|。将式(25)向准弹体坐标系Mxbybzb下分解，得到“×”型正交舵各舵面在准弹体坐标系下产生的加速度矢量为：

(27)

舵面卡死后会引起导弹滚转，对于出现的滚转角ωe，只需令ωm=ωm-ωe，再根据式(26)对各舵面需要承担的加速度分量进行分配即可。

3.2.2其他系统故障

在准弹体坐标系Mxbybzb下，发动机推力对xb方向的机动能力产生影响。正常情况下，发动机以最大推力工作时，在xb方向会产生最大正加速度a+emax，发动机停止工作时，由于空气阻力会在xb方向产生最大负加速度a-emax，因此导弹在xb方向的机动能力为a+emax[k-e,1]，其中k-e=(a-emax/a+emax)<0。

3.3 损伤导弹质心运动方程

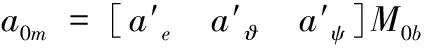
(28)

(29)

式(14)和式(29)构成了完整的导弹有损飞行弹道方程。

4 仿真与分析

4.1 无损飞行弹道

在地面坐标系Ox0y0z0下，取Rm=(0,0,1.0)km，Rt=(16,19.2,0)km，vm=(287,800,-15)m/s(即2.5Ma)，vm=(16,4,0)m/s(即3.2节)，弹目初始距离25 km，导弹在俯仰和偏航方向的最大过载为5g，沿弹体纵轴最大过载10g，最大滚转速度15 (°)/s，目标以恒定速度作圆周规避机动，最大机动角速度ωtmax=1.7(°)/s，导引头时间延迟常数Tk=0.45，弹体阻尼比ζ=0.75，无阻尼振荡频率ω=1.0，仿真步长h=0.01 s，由式(14)和式(29)得到导弹无损攻击弹道。如图7。

图7 无损攻击弹道

导弹无损情况下，最小弹目距离0.043 57 m，脱靶量几乎为零。

4.2 有损飞行弹道

表1中给出了6类典型故障模式实际对应9种故障源(舵面故障时存在4种故障源)，根据二项式定理，共存在29-1=511种故障组合，这里只对单故障源下的飞行弹道进行分析，其他故障模式可首先将对应的故障源叠加然后再进行综合分析。

典型舰载CIWS的最大拦截距离[14]一般在1.5～5 km的范围内，为此假设各种故障发生时，弹目距离均为2.5 km，对于舵面故障，分别取卡死角δci为零和±δmax时的情况进行分析，其余条件同4.1节，由式(14)及式(25)～(29)得到1～4号舵面在不同卡死角δfi时导弹的脱靶量大小L1～L4，结果如表2所示。

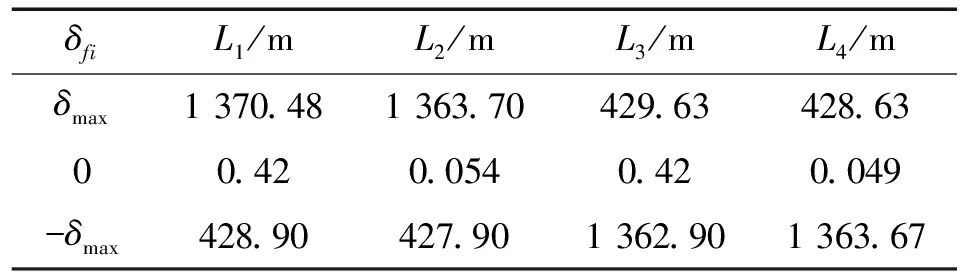
表2 舵面卡死时的脱靶量

图8(a)～图8(d)分别给出了1～4号舵面故障后，对相应攻击弹道的仿真结果，为了便于显示，只绘出了弹目距离小于5 km时的攻击弹道。

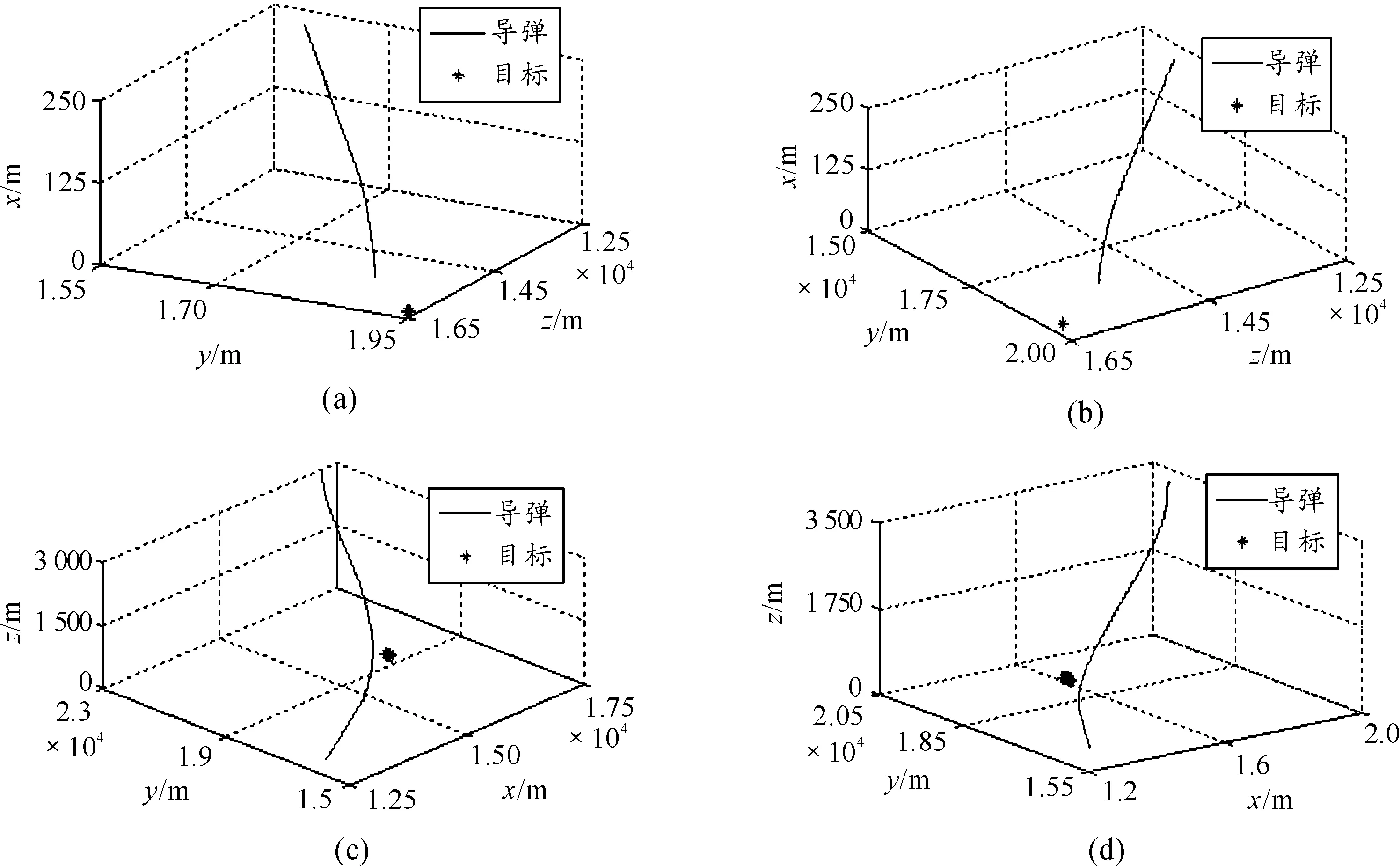
图8 1～4号舵面故障后的攻击弹道

分析表2和图8，当舵面卡死在正最大舵偏角时，1或2号舵面使导弹低头的效应明显，使导弹提前落水，从而引起较大的脱靶量，3或4号舵面使导弹抬头的效应明显，此时脱靶量会较小。当舵面卡死在负最大舵偏角时，情况正好相反。

此外，由于假设正常飞行中导弹滚转角为零，因此1和2号舵面以及3和4号舵面卡死在最大舵偏角位置时，对应的脱靶量分别近似相等。由于末端导弹已经精确对准目标，控制舵指令偏转角很小，因此当舵面卡死在中央位置时脱靶量很小。

对于发动机故障，取k-e=-0.6，由式(14)计算得到kb=0,0.5以及k-e时导弹对目标的脱靶量均位于0.043 60～0.043 61 m之间，可见发动机故障对脱靶量的影响很小。

3～6号部件的故障处理方式同3.2.2节，仿真初始条件同4.1节，由式(14)得到各部件故障后引起的脱靶量，结果如表3。

表3 参数丢失时的脱靶量

图9(a)和图9(b)分别给出了5和6号部件故障后，对相应攻击弹道的仿真结果，为了便于显示，同样只绘出了弹目距离小于5 km时的弹道。对于3和4号部件故障下的飞行弹道，由于脱靶量较小，不再示出。

图9 5～6号部件故障后的攻击弹道

综合表2、表3以及图8、图9，舵面卡死时，脱靶量的大小与卡死角的大小和位置有关，当舵面卡死角较小时，导弹仍然可能命中目标；发动机推力下降后，导弹依然能够在惯性力的作用下飞向目标，对脱靶量的影响不大；在攻击末端丢失目标后，导弹会飞向目标记忆点，依然会保持较小的脱靶量；高度表和加速度计故障后，制导系统会按照错误的参数进行导引攻击，从而造成较大的脱靶量；对于惯导陀螺故障，由于仅仅影响导弹自身的姿态参数，而在末端导弹的姿态趋于稳定，因此基本对命中精度无影响。

5 结论

本文建立了考虑到弹体及导引头动力学特性的三维TNP矢量方程，从系统控制的角度出发，总结归纳出导弹末端突防过程中可能出现的典型故障模式，初步分析了导弹有损飞行弹道，仿真给出了脱靶量，对于分析导弹末端可能的杀伤区域以及舰载CIWS反导靶场实验的安全性评估具有重要的参考作用。

实际情况下，导弹末端突防过程中，各类故障发生的概率以及时间都是不同的，在具体应用中要通过对导弹的易损性分析[15]，建立各类故障的诊断和判读模型，确保为有损飞行弹道的分析研究提供准确的初始化环境。