数学思想在初中数学教学中的应用

摘 要：初中数学知识属于基础教育阶段的关键组成，这一知识的掌握程度会对学生今后的思维发展起到重要影响。而数学知识具有一定的枯燥乏味性，而数学思想作为数学精髓理念，通过在初中数学教学中的应用能够让学生的学习效率有所提高。基于此，文章将主要以初中数学中“数据收集、整理与描述”的内容为例，探讨数学思想在初中数学教学中的应用。

关键词：数学思想;初中数学;教学;应用

数学思想是从数学内容中提炼出来的数学知识的精髓，是将知识转化为能力的桥梁，有着普遍应用的意义，是历年高考的重点。其包括：函数方程思想、数形结合思想换元思想、分类讨论思想。数学学科在整个基础教育阶段中扮演着重要角色，数学思想方法的掌握对其他学科知识的理解也会产生深远的影响。因此，初中数学教师应清醒地认识到数学教学的目的除了要求学生掌握多少知识，更为重要的是让学生懂得如何善于应用数学思想去解决现实问题。下面，笔者结合教学实践，以初中数学中“数据收集、整理与描述”的内容为例，对数学思想在教学中的具体应用从如下几个方面进行简要分析。

一、 函数方程的数学思想

函數的思想就是在解决问题的过程中，把变量之间的关系抽象成函数关系，把具体问题转化为函数问题，通过对函数相应问题的解决，便可达到解决具体问题的目的。方程的思想，就是从分析问题的数量关系入手，把变量之间大联系用方程的关系来反映，然后通过解方程或对方程进行讨论的方法，使问题得到解决。在数学思想方法中，函数方程思想属于常用且关键的一种，主要是利用数学问题中的已知量和未知量的关系去构建存在等量关系的方程，然后在方程的求解转化中去解决问题。在对数据的收集与整理过程中也会用到函数方程的数学思想，也即是结合已知的数据和逻辑对未知的数据进行反向补充。利用函数方程数学思想的核心体现在要找准各个数据间暗藏的数量关系，将存在等量关系的已知数据与未知数据进行罗列，采取逆推的方法去求出未知量，保证问题有效解决。在“数据收集、整理与描述”的问题解决中，特别是遇到数据分析类的题目时，函数方程数学思想的应用则更加有优势。

例如，某班一共有20名学生，在期末考试中得100分的2人，70分的5人，60分的1人，而80分和90分的人数未知，已知此次期末考试的班级平均分为82分，结合这部分数据去分析80分和90分的人数具体是多少。基于此，我们可列出方程1+5+2+x+y+2=20，（60+70×5+80×x+90×y+100×2）÷20=82，通过求解方程便能够计算出此次期末考试中得到80分的人数为5人，而90分人数为7人。不难看出，函数方程的数学思想核心在于将具象化的事物抽象为数学符号，通过对数学符号列出的方程进行求解，便能够得出具体的量去表示具象事物，掌握这一数学思想方法，在解决这类数学问题时便能得心应手。

二、 数形结合的数学思想

数形结合思想就是把抽象的数和直观的形双向联系与沟通，使抽象思想与形象思维有机地结合起来化抽象为形象，以期达到化难为易的目的。将代数与图形进行有机结合，不仅能够运用代数去解释并解决图形问题，简化该类问题的解决难度;同时也能够运用图形去解决代数问题，让代数问题变得更加直观形象。在初中数学的“数据收集、整理与描述”内容中存在众多图表，运用数形结合的数学思想方法能够让数据以更加直观的方式呈现出来，这种方式要比过去纯粹用文字进行描述要更好理解，并且计算起来会更加简便。

比如，在教师所布置的“家庭用电调查”的数据统计分析课后作业中，学生通过对数据的收集与整理，要想从繁多数据中找出其中的规律会显得毫无头绪，此时教师可引导学生巧用数形结合思想方法，将所有数据转化为柱形图或扇形图进行呈现，经过图形的对比便能明显察觉其中的差异与规律，同时也能进一步深化学生对统计图的理解。此外，三角函数及其对应的图形也是数形结合数学思想的重要体现，初中学生也需要掌握函数及其图形变换的知识点，比如平移、翻转、对称等，这些知识的掌握对于学生实际问题的解决，能够发挥事半功倍的效果。

三、 分类讨论的数学思想

所谓分类讨论，也即是结合问题本身的已知条件去进行分类，而如何且为何进行分类，这部分内容则要求教师在教学活动开展中去引领学生自主探究与感悟。分类讨论的思想就是整体问题化为部分问题来解决，它是逻辑划分思想在解数学题中的具体运用。分类讨论的数学思想并非一朝一夕便能养成，需要通过长时间的渗透，才可逐步提升学生的归纳总结能力。数据整理也即是利用分类讨论的数学思想对所收集的数据进行描述，把所有性质存在差异的数据分类到不同的类别当中，并且划清不同类别的界限，从而将问题由整体划分为具体的多个子问题，能够显著提高解题的效率。

以下列题目为例，“数据的收集整理”是基于学生已经积累一定的认数、计算以及把一些物体简单地分类整理的知识的基础上学习的，通过教学让学生学会用调查法经历简单的数据收集、整理、描述和分析过程，为学生进一步学习统计与概率领域的内容打好基础。

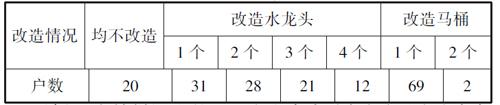
政府部门投入资金用于老城区的水龙头和马桶改造，某一社区在完成政府该项工作的过程中，对抽样调查的120户人家的改造需求进行了数据收集，汇总之后形成下表：

改造情况均不改造

改造水龙头改造马桶

1个2个3个4个1个2个

户数2031282112692

请问：在抽样调查的120户人家中，同时需要改造水龙头与马桶的户数为多少？

分析：结合数据汇总表以及题意不难看出，我们可将整个120户分为均不改造、只改造水龙头、只改造马桶、均改造水龙头和马桶的四个类型，所以可列出方程式，设置均改造水龙头和马桶的户数为x，那么只改造水龙头的户数为92-x，只改造马桶的户数为71-x，从而得出x+（92-x）+（71-x）=120-20，进而得出x=63。通过分类讨论数学思想的应用，能够得知均改造水龙头和马桶的户数为63户。

综上所述，数学思想作为初中数学教学中的重点，需要引起所有教育工作者的重视，通过在教学活动中渗透对数学思想的应用，去有意识地培养学生的数学思想能力，从而提高学生运用数学思想去解决实际问题的意识，如此一来才能够真正地提高初中数学教学质量与效率。

参考文献：

[1]孔凡哲，刘帅.感悟数据的收集、整理与描述[J].中学生数理化（七年级数学），2016（6）：5-6.

[2]高亚如.数形结合思想方法在初中数学教学中的应用研究[D].聊城：聊城大学，2018.

作者简介：

陈开元，福建省漳州市，福建省漳浦县丹山中学。