大学微积分课程的延伸——分数阶微积分

宋 传 静

(苏州科技大学数理学院，江苏 苏州 215009)

一、引言

微积分由德国人莱布尼茨(Gottfried Leibniz，1646-1716)与英国人牛顿(Issac Newton，1643-1727)分别独立发明，它是大学里的一门基础课程，它的思想和方法无处不在[1][2]。自从牛顿、莱布尼茨建立微积分，经过几百年的千锤百炼，微积分已形成一整套经典的理论框架和表达方式。目前为止，大学生接触到的微积分，指的都是整数阶的微分和积分[1][2]，关于微积分方面的教学改革也都是基于整数阶微积分给出的[3][4]。微积分课程一旦结束，学生便认为已经掌握了所谓的微积分学。实际上，分数阶微积分也是存在且有重要意义的，此时所求微分或积分的阶次就会由通常的整数变为分数。学生的学习不能止于经典，给学生留下思考的空间是很有必要的。因此，在学生已掌握一元函数与多元函数的整数阶微分学与积分学后，可适当给学生介绍些微积分的应用或后继发展，例如分数阶微积分的概念及其应用。

以左Riemann-Liouville型分数阶微积分为例的教学已在课堂上实践过，课堂上介绍了分数阶微积分的基本概念，并举例说明其用法及性质。本科生课堂上讲到的关于分数阶微积分的知识将在下面列出来，希望能够抛砖引玉，激发大学生及研究生对微积分的内容作进一步的探索。

二、预备知识

先介绍两类特殊函数：Gamma函数和Beta函数，它们在分数阶微积分的定义及运算中经常用到[1][7]。

(1.1)Γ(z+1)=zΓ(z)，Γ(-n)=，

n=0,1,2,…

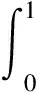
三、左Riemann-Liouville分数阶微积分

1.左Riemann-Liouville分数阶积分

设u(x)为一函数，x∈(a,b)，μ>0，则

称为次数为μ的左Riemann-Liouville分数阶积分[7]。

由这个定义可得：

第一，当μ=n为正整数时，有

在一般的教科书上，上式表示对函数u(t)求普通意义下的n重积分，即普通意义下的积分是分数阶积分的特殊情况。

第二，定义中，令a=0，则当u=1/2时，可得

当u=1时，可得

当u=3/2时，可得

由此可看出，左Riemann-Liouville型u阶积分是一种加权积分，其中u<1时，积分变量ξ距离积分上限t越远，其对应的权值越小；u=1时，其权值恒为1；u>1时，积分变量ξ距离积分上限t越远，其对应的权值越大。

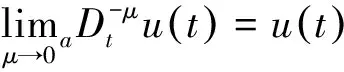
第四，左Riemann-Liouville型分数阶积分满足如下线性关系

2.左Riemann-Liouville分数阶导数

左Riemann-Liouville分数阶导数是通过将普通意义下的导数与左Riemann-Liouville型分数阶积分算子作复合运算得到的。

设u(x)为一函数，x∈(a,b)，μ>0，n是大于μ的最小整数，则

称为次数为μ的左Riemann-Liouville分数阶导数[7]。

由这个定义出发，可得：

第一，当μ=n为正整数时，

当μ=n-1为正整数时，

即普通意义下的导数(整数阶导数)是分数阶导数的特殊情况。

第二，左Riemann-Liouville型μ阶导数也可视作一种加权积分，积分变量ξ距离积分上限t越远，其对应的权值越小。也正因如此，分数阶导数被认为具有记忆性。

第三，左Riemann-Liouville型分数阶导数满足如下线性关系

四、举例说明

课堂上共给出如下3个例题，它们均是从文献[7]中整理组织的。

例4.1 当t>a时，求u(t)=C(C为常数)的μ阶左Riemann-Liouville型分数阶积分和导数，其中n-1<μ

解：由左Riemann-Liouville型分数阶积分和分数阶导数的定义可得

特别地，当a=0，μ=1/2时，可得

由例4.1可以看出，Riemann-Liouville型分数阶意义下，对常数求导不为零，而普通意义下(整数阶求导)，常数的导数为零。因此，Riemann-Liouville型分数阶微分与整数阶微分之间有一定的差别。从这个意义上来说，引入分数阶微积分的概念是对传统微积分的一种完善和补充。

例4.2 试求函数u(t)=(t-a)ν，ν>0的左Riemann-Liouville型分数阶积分和导数。

解：由左Riemann-Liouville型分数阶积分的定义出发，并令τ=(ξ-a)/(t-a)，则有

再由左Riemann-Liouville分数阶导数的定义可得

特别地，当a=0，u(t)=t，μ=1/2时，可得

解：利用例4.1和例4.2的结果可得

由此可得

即左Riemann-Liouville型分数阶积分算子满足交换律。实际上，这个结论是始终成立的，即对于任意的μ,ν>0，

这个结论可以用左Riemann-Liouville型分数阶积分的定义进行证明，这里就省略了。

同理可得，左Riemann-Liouville型分数阶导数不满足交换律，只有当函数u(t)满足一定的条件时，分数阶导数之间的运算才能满足交换律，这里也不详细介绍了。

五、结论

课堂上只简单给出左Riemann-Liouville型分数阶微积分的定义，并举例说明其用法。实际上，分数阶积分的连续性与绝对连续性定理、分数阶微积分的莱布尼茨公式、分数阶微积分的中值定理等均已有研究。除此之外，右Riemann-Liouville型分数阶微积分及Caputo型分数阶微积分的相应成果也均有研究，感兴趣的同学可以阅读相关资料进行了解。