利用平移对称性分析带电粒子在电磁场中的运动问题

杨钧捷

(江苏省海门中学,江苏 南通 226100)

带电粒子在电磁场中的一些运动问题中,电磁场区域往往具有空间平移或旋转对称.在这类问题中,若运动轨迹的几何分析较为复杂时,可利用对称性结合动量定理或角动量定理寻找守恒量的方法来分析,往往能使问题得到较为简洁的处理.

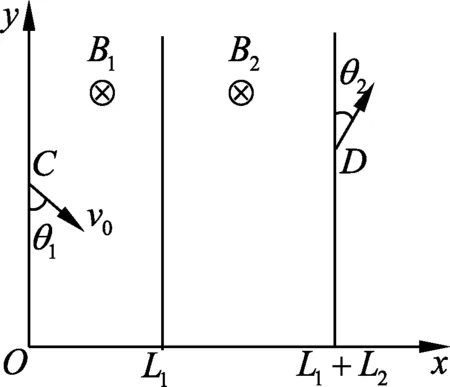
图1

例1.如图1所示,xOy平面内有两个相邻的带状匀强磁场,方向垂直xOy平面向下,磁感应强度大小分别为B1、B2,磁场区域宽度分别为L1、L2,一带正电的微观粒子(+q,m)从磁场B1区域左边界C点以θ1角度进入,从磁场B2区域右边界D点以θ2角度离开.求粒子的初速度v0.

解析:粒子初速度大小未知,粒子运动的圆心位置和离开磁场B1区域右边界的位置均不确定,用几何方法分析较为繁琐.考虑到磁场区域具有y方向的平移对称性,可以用动量定理进行分析.

设粒子在B1=-B1k区域右边界N点出射并进入B2=-B2k区域,由py+qxB守恒得

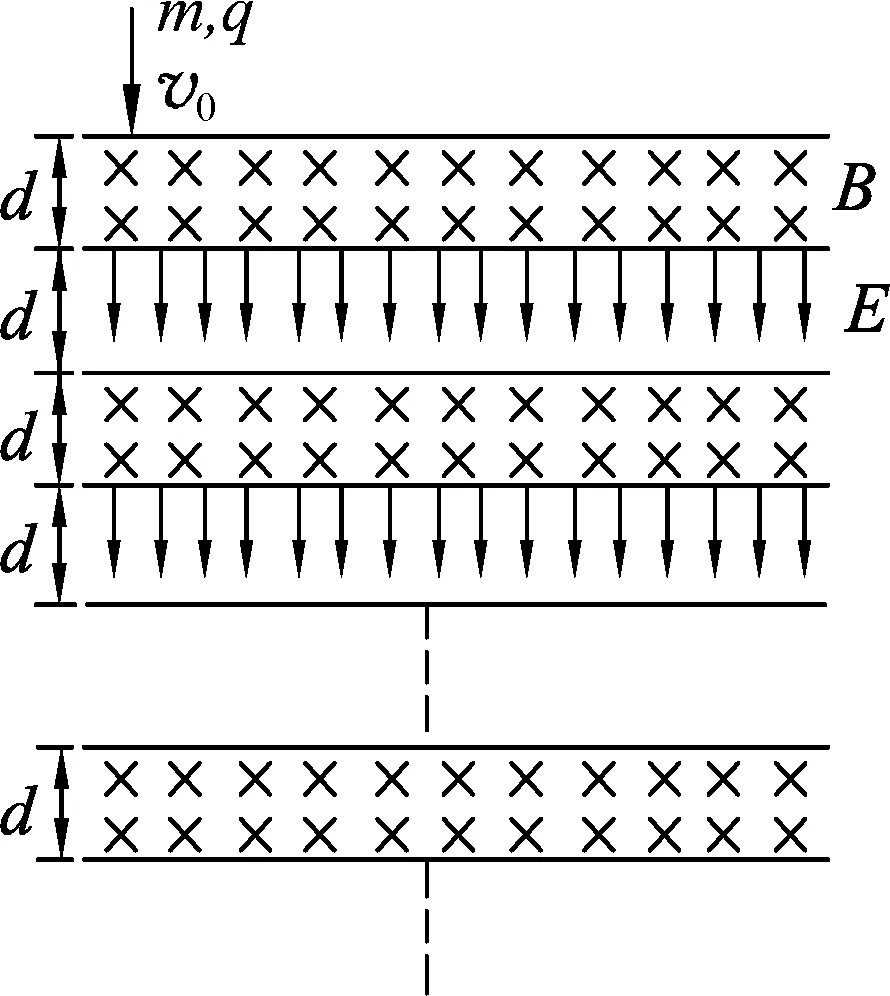
图2

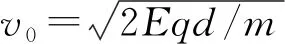
解析:本题是一道组合场问题,粒子在磁场和电场中都发生偏转,运动复杂,若用常规方法将涉及到数列问题,较为繁琐;若考虑到电磁场区域具有水平方向的平移对称性,利用动量定理分析将变得简易.

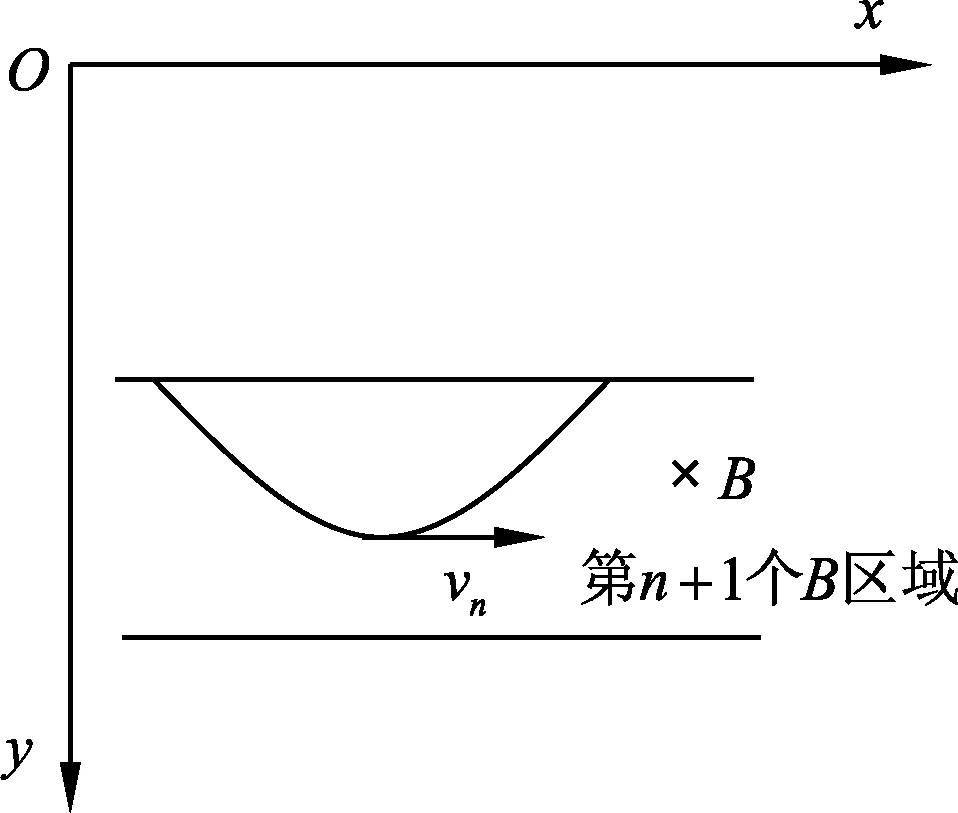
图3

电磁场区域具有x水平方向

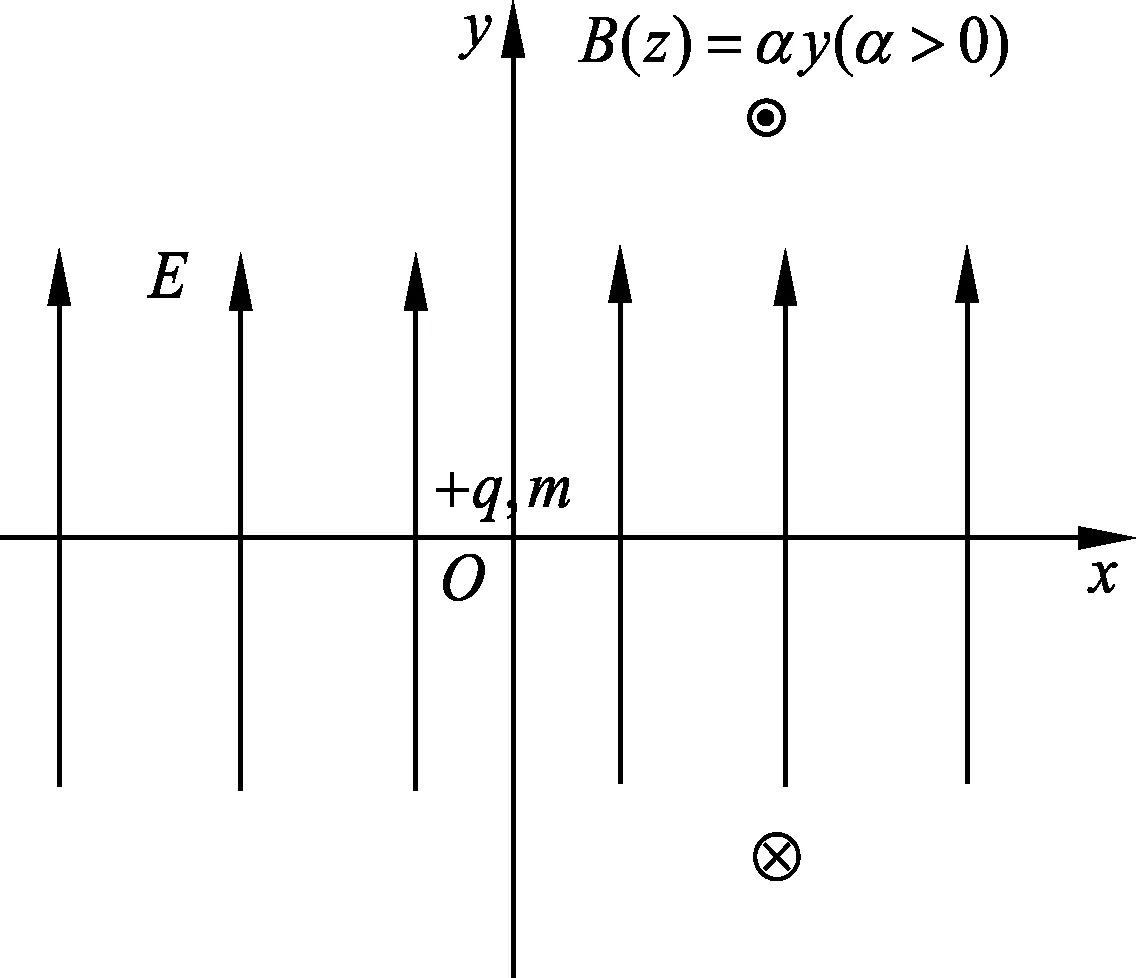
图4

例3.如图4所示,空间存在相互正交的电磁场,匀强电场E沿y轴正向,非均匀磁场B(z)垂直于xy平面,磁感应强度B(z)=αy(α>0),质量为m、电荷量为+q的微观粒子在坐标原点O静止释放,求粒子运动过程中y轴方向的最大位移.

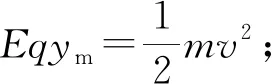
小结:带电粒子在具有某方向平移对称的电磁场区域做平面曲线运动时,有两个自由度,可以选用动能定理和平移对称方向的动量定理来列出两个独立方程进行分析求解,避开了可能较为繁琐的粒子复杂轨迹的几何分析．此种方法体现了物理学中的对称与守恒的思想.