运动多桨舰船在浅海中的轴频电磁场计算及仿真∗

田永民 李忠猛

（1.92515部队 葫芦岛 125000）（2.海军工程大学 武汉 430033）

1 引言

在应用轴频电磁场信号作为新型鱼水雷武器的引信时必须面临的一个问题是：由舰船产生的轴频电磁场（场源）是相对于水雷（场点）运动的，而运动场源和静止场源产生的电磁场是不相同的［1～5］。在假定各层媒质为线性均匀、各向同性媒质的前提下，利用Hankel变换方法推导了水平成层导体半空间中位于顶层的静止时谐垂直电偶极子在该层产生的电磁场的一般表达式。文献［6］中只给出了在各层介质磁导率相同时的两层、三层介质模型中低速运动的垂直时谐电磁场的表达式，具有一定的局限性。通过改变在对n层导电介质中静止的垂直时谐电偶极子电磁场表达式的推导方法，得到了n层导电介质中位于顶层运动的时谐垂直电偶极子在该层产生的电磁场的一般表达式。该表达式可应用于不同情况下浅海电磁场建模。考虑到大型船舶一般采用多桨推进，本文以三层介质模型为基础对多桨推进船舶在浅海中的电磁场进行建模及仿真。

2 电磁场时谐理论

2.1MAXWELL方程组时谐形式

MAXWELL方程组时谐形式如下：

上面得到的B、E变量均是频域的量。将这些频域内的量转换为时域内的量［6］，转换公式为

2.2 电磁场的相对性原理

如图2所示，坐标系S′沿x轴负方向以速度v相对于坐标系S运动。其中两坐标系S和S′的x轴重合。y轴和z轴相互平行。当两坐标原点O和O′重合的时刻，取t=t′=0 。

根据文献［7］，由洛仑兹时空变换公式可以得出在图2坐标系中的电磁场变换公式为［7］

3 运动时谐垂直电偶极子在成层介质中的矢量磁位

选取直角坐标系o-xyz，如图1所示，以坐标面z=d0，d1，d2，...，dn-1(d0＜d1＜d2＜ … ＜dn-1) 为 边界面，图2为n层导电介质在y=0的平面上，以速度v沿x轴正方向水平运动的运动时谐垂直电偶极子，电偶极子的初始位 (t=0)为 (x0，0，z0)，则运动场源在任一时刻的位置为(x0+vt，0，z0)，静止的场点所在位置保持R(x，y，z，t)不变。另外，图2中还建立了n层导电介质中运动垂直时谐电偶极子的洛伦兹坐标系。

将运动时谐电偶极子看作某一时刻下在图2的坐标系S中静止的场源，需求出某时刻t下位于点R′(x0+vt，0，y0)的静止场源在场点R(x，y，z，t)处产生的电磁场。

该静止的电偶极子在介质1中的电流密度表达式为

图1 n层导电介质模型下的示意图

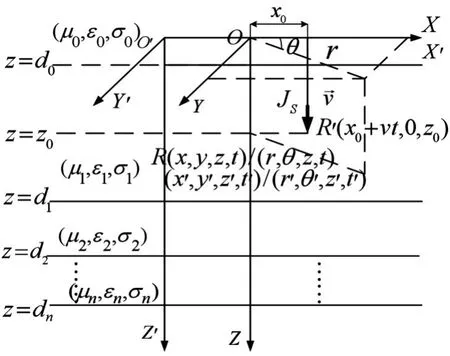
图2 n层导电介质模型下的洛伦兹坐标系

处于任意位置的静止的垂直时谐偶极子的矢量磁位A仅包含z轴方向的分量，即

因此，在0，1，…，n区的矢量磁位分别满足约束方程如下所示。

求解上述方程组，可得到n层导体半空间中顶层导电媒质中的矢量磁位为［8～13］

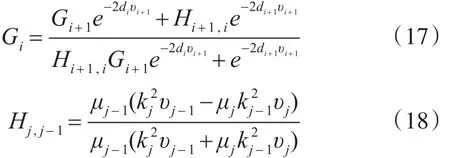
4 运动时谐垂直电偶极子在浅海中的电磁场

4.1 单个运动时谐垂直电偶极子在浅海中的电磁场

在不同的浅海条件下，可利用不同的导电媒质模型计算其电磁场。本文以三层模型对浅海导电媒介进行建模，因此有n=2，d2→∞，d0=0。

根据式（16）得到

由此可得标量磁位具体公式，同时，可根据式（2）（3）计算电磁场。

4.2 多个运动时谐垂直电偶极子在浅海中的电磁场

对于多个垂直电偶极子在同一点产生的电磁场而言，每个垂直电偶极子产生的电磁场具有三个分量。本文采用基于Hankel变换的快速FFT算法可以求解该电磁场表达式的频域及时域形式。任意时刻t电磁场量可记为：Bx1t、By1t、Bz1t、Ex1t、Ey1t、Ez1t，Bx1tt、By1tt、Bz1tt、Ex1tt、Ey1tt、Ez1tt，由此可得n个垂直电偶极子产生电磁场表达式如下所示。

电场x分量为

磁场x分量为

以上各式可用于计算电磁场x分量，其余分量计算方法同上。

5 浅海中多桨推进舰船电磁场仿真

现役大型舰船需多桨推进，而轴频电磁场正是由于旋转的螺旋桨对电流进行调制而产生的。由于各螺旋桨转速及开始转动的时刻的不同，其产生的电磁场也是不同的。本文将给出双桨推进舰船电磁场仿真结果。

5.1 基于不同相位的轴频电磁场仿真计算

对于双桨推进的运动舰船在航行的过程中，假设两桨的转速相同，但是两桨的相位不同，舰船的运行速度为5m/s。这里可以用两个频率相同的运动垂直时谐偶极子对舰船的轴频电磁场进行建模。如图2建立三层模型，分别为：空气、海水、海床，其参数如下：ε0=(1/36π)×10-9F/m ，σ0=0 ，μ0=4π×10-7H/m ，σ1=4Ω/m ，ε1=80ε0，μ1=μ0，σ1=0.04Ω/m ，ε2=8ε1，μ2=μ1。垂直时谐偶极子频率为2Hz，强度为1A·m，起始坐标为（x=-1000m，y=0，z=10m），结 束 坐 标 为（x=-1000m，y=0，z=10m）。本文主要给出x分量的仿真结果。

图3 相位不同步时电场x分量的时域与幅值图

通过分析仿真结果，可以知道：

1）对比图3（a）（c）可知：θ角度的变化并不影响轴频电场的幅值。

2）对比图3（a）（b）（e）（f）可知：当相位相同时，两个相同强度的电偶极子产生的电磁场时域值是单个同参数电偶极子的2倍。

3）对比图3（a）（b）（c）（d）可知：当相位相同时，轴频电磁场达到最大；当相位相反时（θ1=0，θ2=π），轴频电磁场达到最小；这也说明了轴频电磁场由于相位不同而存在抵消效应。

5.2 频率不同时产生的轴频电磁场

以两个具有不同频率的垂直时谐偶极子进行电磁场仿真计算，分别设其频率为：f1=3Hz，f2=2Hz，计算可得如下结果。

图4 频率不同时电场各分量的时域与幅值图

通过分析仿真结果，可得如下结论：

1）由图4（a）（b）可知：电场z方向由于频率的不同导致有较大的幅值差异。

2）由图4（c）可知：电磁场的包络线没有频率相同时光滑（如图3所示），这说明频率对轴频电磁场的时域值有较大的影响。

3）由图4（a）（b）（c）可知：提出当频率不同时的轴频电磁场的建模思路：首先求出两个桨产生的不同的轴频电磁场频率，然后采用具有这两个频率的时谐偶极子对轴频电磁场进行建模。

6 结语

本文针对运动垂直时谐电偶极子在n层导电介质中的电磁场分布问题，建立了对应的洛伦兹模型，推导获得电磁场的矢量磁位表达式。为了对浅海中多桨推进舰船轴频电磁场进行建模，本文建立了三层简化模型。最后，本文设计了浅海中多桨推进运行舰船轴频电磁场在不同相位及不同转速条件下的仿真实验，并对结果进行了详细的分析，仿真结果验证了本文推导的轴频电磁场计算方法的有效性。

［1］Jianhua W，Guangzhou L，Yongsheng L．Simulation and measurements of extra low frequency electromagnetic field［C］//Conf．Proc．UDT Europe，2004.

［2］Hubbard J C，Brooks S H，Torrrance B C．Practical mea⁃sures for reduction and management of the electro-magnet⁃ic signatures of in-service surface ships and submarines［C］//Conf．Proc．UDT Europe，1996：64-65.

［3］Dymarkowski K，Uczciwek J．The extremely low frequen⁃cy electromagnetic signature of the electric field of the ship［C］//Conf．Proc．UDT Europe，2001：1-6.

［4］Hoitham.P et al，Electromagnetic signature modeling and reduction［C］//Conf.Proc.UDT Europe 99，97

［5］Bostick.F.X，H.W.Smith.H.W，Boehl.J.E.，The de⁃tection of ULF-ELF emissions from moving ships［C］//ADA037830，1977.

［6］毛伟，周萌，周耀忠.浅海中运动时谐垂直的电偶极子产生的电磁场［J］.哈尔滨工程大学学报，2010，12（12）：1580～1586.

［7］Sun Xin yao.The relativity principle of electromagnetic field.Joural of Huzhou normal university［J］.1996（5）：28-31.

［8］卢新城，龚沈光，周骏，等.深海中极低频时谐垂直电偶极子电磁场的解析解［J］.武汉理工大学学报（交通科学与工程版），2003，6（6）：746-749.

［9］卢新城，龚沈光，周骏，等.海水中极低频水平电偶极子电磁场的解析解［J］.电波科学学报，2004，19（3）：290-295.

［10］刘胜道，龚沈光.并矢格林函数法求解海水中电偶极子电场［J］.电波科学学报，2002，17（4）.374-377.

［11］卢新城，龚沈光，陈新刚.水平n层导电介质中时谐垂直电偶极子的电磁场［J］.地球物理学进展，2004，19（3）：596-601.

［12］LU Xin-cheng，GONG Shen-guang，ZHOU Jun，et al．The electromagnetic field of a time-harmonic HED em⁃bedded in an n-layerconductinghalf-space［C］//Asia-Pacific Conference on Environmental Electromag⁃netics CEEM’2003，173-177.

［13］肖春燕，雷银照.分层球形导体中任意位置直流电流元产生电位的解析解［J］.物理学报，2005，54（4）：1950-1957.