未满水覆杯实验成败的计算分析

阳 丽 白克钊 胡卓坤 张妙静 荣 家

(广西师范大学物理科学与技术学院,广西 桂林 541004)

图1 未满水覆杯实验

“覆杯实验”是常被用以验证大气压存在的一个实验．而未满水覆杯实验内容为(图1):在玻璃杯中装一定高度的(未装满)水,用盖片将杯口盖好,用手按住将杯子倒置使得杯口向下,然后轻轻松开,当水杯倒置之后盖片仍然稳稳地“粘”在杯底,实验成功．否则杯中盖片和水下落,实验失败．

1 未满水覆杯实验的研究现状

学者们对于覆杯实验原理的分析主要有3种观点:[1-8]一种认为实验成功的原因是水的表面张力托住杯中的水、纸片以及纸片下(吊起的)重物;[1]一种认为水的表面张力并不是实验成功的唯一原因,是外界大气压、液柱压强、表面张力形成的综合作用才使得实验成功;[2-4]大部分学者则认为覆杯实验中表面张力的作用非常之小,可以忽略不计．[5-7]杯子倒置后,在杯内水的重力作用下,盖片会下沉,从而使杯子里的水向外渗出,杯内气体压强变小,于是杯内外气体就有一定的压强差,这就是覆杯实验中托住水和盖片的主要原因．于是部分学者对覆杯实验做了定量计算,例如,文献[8]分析了水沿处的表面张力、间隙水层的高度、水深度和纸片的渗水性对覆杯实验成功的影响,并计算了水层间隙存在的最大值,认为只要杯子高度足够低,杯内水很多或者很少的时候,覆杯实验都可以成功．文献[9]认为纸片的浸润对实验的成功没有影响,以及表面张力的作用非常之小,可以忽略不计．实验成功与杯子的长度和空气柱长度有关,用玻意耳定律计算了杯子高度和空气柱的高度、压强之间的关系,认为杯子越长,空气柱越长,实验容易失败,反之,实验容易成功;文献[10]利用纸片上下的压强差,加上凹液面内外压强差与附着层水对凹面的表面张力平衡方程计算了极限情况下杯内的空气柱长度．他认为即便杯中空气柱长度占据总长的4/5甚至更多,实验依然可以成功．文献[11]认为半杯覆杯实验成功的原因是由于卡片微小的下移,他估算了下移高度的数量级并给出了几点做好覆杯实验的经验．文中认为用杯壁宽的杯子做实验,成功率高．因为杯壁越宽,更有利于防止漏气．

总之,在以往的研究中普遍认为覆杯实验成功是由于杯子内外的压强差托住了水和纸片,当实验失败的时候,大气压不能托住水和盖片,从而盖片和水分离并落下．

2 未满水覆杯实验原理分析

通过运用显微镜多次观测未装满水的覆杯实验后,发现了一些非常重要的细节．首先,覆杯实验失败时,盖片与水并没有分离,而是水和盖片一直粘附在一起,共同下落(图2);其次,覆杯实验失败时,空气沿杯口由液桥上方进入杯中,之后气泡逐渐上升且变大,然后水和盖片同时一起下落．覆杯实验失败的直接原因是此时液桥内部的压强与表面附加压强之合小于大气压强,使得空气不断进入杯中,从而无法形成稳定的液桥．

图2 实验失败过程高速摄影图

现对未满水的覆杯现象进行分析:倒置前杯子里面的气体压强为大气压,倒置瞬间,由于杯口压强大于大气压强以及杯内水的重力作用,杯子里的水就会往外流,盖片下降,导致杯内气体的体积增大,压强减小,杯口与盖片出现间隙(即水层,如图3所示),这个间隙称为液桥．[12-13]本文针对水对盖片润湿,但盖片不被水渗透的情况进行分析．由于水的润湿性,实验中放手前盖板与杯口的紧密程度不同,液桥有几种形状.本文关注图3情况．由于周围大气压压迫间隙的水,当不考虑液桥那部分的重力的时候,压差是一个常数,即液桥液面在铅直平面形状是等曲率表面,形成侧边弯月面(凹面如图4所示)．图4为实验示意图．为了分析方便,液桥的比例被夸张放大．直圆柱形水杯内部高为H,半径为R,横截面积为S,正立时加水高度为h,倒置后杯内水的高度为h′,塑料盖片的重量为G,杯口和水层之间的高度为D,液桥凹面的半径为r,水与玻璃杯的接触角为θ1,水与塑料盖片的接触角为θ2.

图3 显微镜下实验现象图

图4 实验示意图

2.1 平衡条件

由于水和盖片接触,水和纸接触的部分就存在表面张力,表面张力方向与液桥的凹液面相切,力的方向竖直向上,但是表面张力的数值较小,并不能支撑杯内水的重力．还需要考虑附加压强的作用,即纸片会受到向上的毛细力的作用．毛细力是内外压差引起的吸引力和轴向上液体表面张力之和,[13]其中液体的表面张力利用公式F=γ×C(γ为液体表面张力,C为杯子的周长)进行计算,内外压强差可由Young-Laplace方程计算:

(1)

其中r′和r是液桥表面的主曲率半径．r′是方位半径,r是子午半径(图4中液桥凹液面的半径)．

作用在盖片上的毛细力可以写为

F毛细=πx下2Δp+2πγx下.

(2)

当盖片不掉下时,以盖片为研究对象在竖直方向可写出平衡方程:

p0S下+F毛细力=p底S下+G,

(3)

其中p0为外界大气压强,F毛细力为液体与盖片之间的毛细力,表现为向上的引力．p底为液体底部对盖片的压强．S下为液体与盖片的接触面积,其中

S下=π(R+rsinθ1-rsinθ2)2，

(4)

p底=p1+ρg(h′+D),

(5)

D=rcosθ2+rcosθ1.

(6)

液桥的体积为

(7)

其中x,y表示液桥上任意一点处的横坐标和纵坐标的数值．

x=R+rsinθ1-rsinθ,y=rcosθ2-rcosθ．

得到液桥的体积为

V=r3I+r2J+rK,

(8)

其中

k=π(cosθ1+cosθ2)R2.

由于杯子倒置过程时间较短,可近似看成等温过程．倒置前杯内气体压强为p0,倒置后杯内气体的压强为p1,根据玻意尔定律可以得

p0S(H-h)=p1S(H-h′),

可得

(9)

联立公式(1)-(9)式即可以解出P1、r、h′和D的数值．

当杯子倒置之后形成液桥,空气指向液体内部的压力压迫液桥水面,形成凹面,液桥外部压强为大气压强p0,p0=p液桥内部+Δp,由公式(1)可计算出内外压强差Δp=γ(1/r-1/r′)．此时液桥上部(即杯口处)pM=p1+ρgh′．

当p0-Δp≤pM时,实验成功．

当p0-Δp>pM时,实验失败,此时杯口出有空气泡进入,气泡半径会迅速增大, 形成一个往上升的气泡, 从而使水沿着杯子内壁流出．

2.2 计算结果

实验中用的盖片质量为5 g,杯子直径6 cm．纯水在20 ℃温度下的表面张力系数为0.0728 N/m,θ1=37°,θ2=60°．[14]

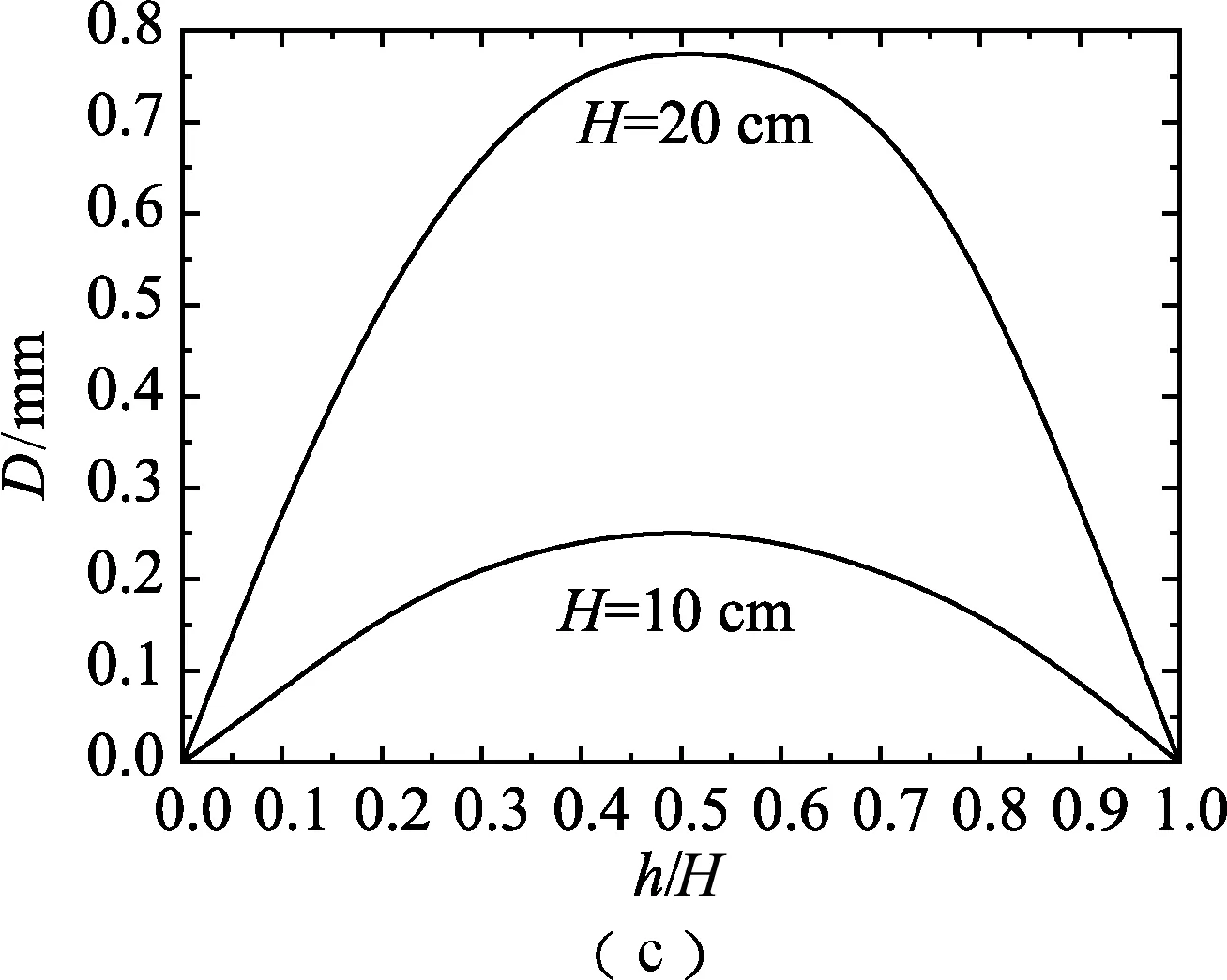
图5 计算结果

对上述方程进行数值计算,计算结果如图5所示．杯子倒置之后,杯内水下降的高度Δh/H,盖片下移的高度D,子午半径r均随着水深比h/H呈现了非线性变化,其变化规律一致,曲线都是先增大后减小,Δh,D,r与h/H关系曲线对于h/H=0.5存在对称性．(p0-p1)/p0随h/H增加呈现出线性增加的规律．

当h/H→0时,接近空杯情况下,倒置之后,杯内水柱下降的高度Δh,D,r不大,杯内空气压强(p0-p1)下降也不大．而当接近满水情况下,即h/H→1时,p0-p1→ρgh．倒置之后杯中水位只要下降一点点就会导致p1急剧下降．此时,盖片外部和杯内空气的压强差(p0-p1)/p0最大,曲线剧烈变化从而大气压足以将卡片牢牢地压在杯口上,甚至把盖片推向杯内．盖片为纸片时此现象非常明显,纸片的中心微微地向杯内凸出．

图5中Δh,D,r与h/H关系曲线对于h/H=0.5存在对称性．图5中当h/H=0.5,即水深是杯子高度的一半时,杯内水下降高度Δh最大,同时盖片下移高度D和液桥侧面子午半径r也最大,最易导致实验失败,这与文献7结论一致．此时杯口处液体内部压强最小,空气最易挤入杯内．相对而言杯内水柱h大于或者小于半杯水的高度时实验较易成功．

图5(c)中可见对于不同H的杯子而水深比h/H一样的时,高杯子倒置之后杯内水下降的高度比Δh/H大一些．这说明水深比h/H一样时,高杯子做覆杯实验较难成功．

3 结论

综上所述,未满水覆杯实验成败的关键在于是否能够保持液桥的稳定,尤其是液桥侧面的稳定.这不但要求液桥侧面要求满足平衡条件,对于扰动也要有一定的“抵抗力”．往往实验失败的原因在于下移高度大,导致抗扰动能力下降,使得空气进入杯内,进而使得实验失败．研究表明用半杯水做覆杯实验时,实验最容易失败;相同水深比时,高杯子做实验,成功率较低．