利用GeoGebra绘图实现全参数可调的振动与波的叠加演示
王洪涛 石礼伟 李 艳
(中国矿业大学物理科学与技术学院,江苏 徐州 221116)
采用计算机辅助手段生动、直观、动态、全面的演示抽象、晦涩的知识点是符合时代特征和学习认知规律的.[1-2]GeoGebra是一款包含了几何、代数、表格、图形、统计和微积分等功能的自由的跨平台的动态数学软件,不仅可以方便地通过鼠标点击进行简单的几何绘图,也可以通过代数及指令输入精确绘制复杂的图形,而且能够方便地通过变量滑动条实现几何图形的动态变化演示. 在物理学的具体教学过程中引入GeoGebra,充分发挥其在多功能几何绘图上的优势,直观形象、生动全面地演示抽象的物理知识,对教学效果会有很大的帮助和提升.[3-5]
1 振动的叠加动态演示
简谐运动就是从一般振动中概括出来的最基本的振动形式,而振动的叠加则是完成由简谐运动拓展到一般振动的纽带,因此振动的叠加在教学中是一个很重要的知识点. 而振动的叠加原理只是明确某一时刻合振动的位移等于各分振动在同一时刻振动位移的矢量和,理解起来比较抽象. 利用GeoGebra动态数学绘图软件则可以生动直观地演示叠加的结果,并且可以灵活地调节各个参数改变输出结果,使学生能够深刻、全面地了解振动叠加结果与各物理量之间的关系.
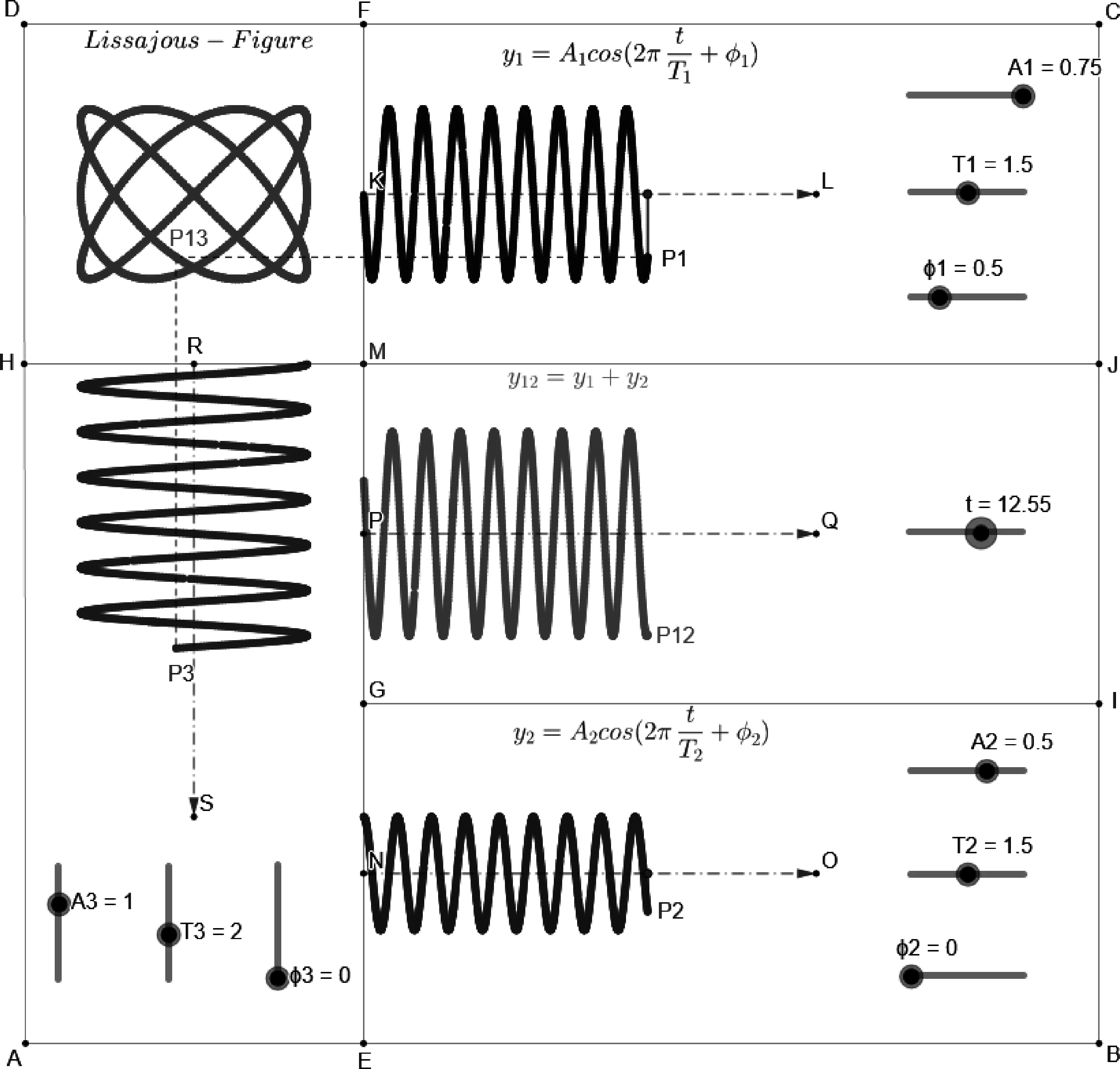
简谐运动方程包含了4个参数,振幅A、周期T、初相位φ以及时间t,所以开始绘图时先建立如图1所示共计10个参数滑动条,确保叠加结果全参数可调,各参数具体取值见表1.
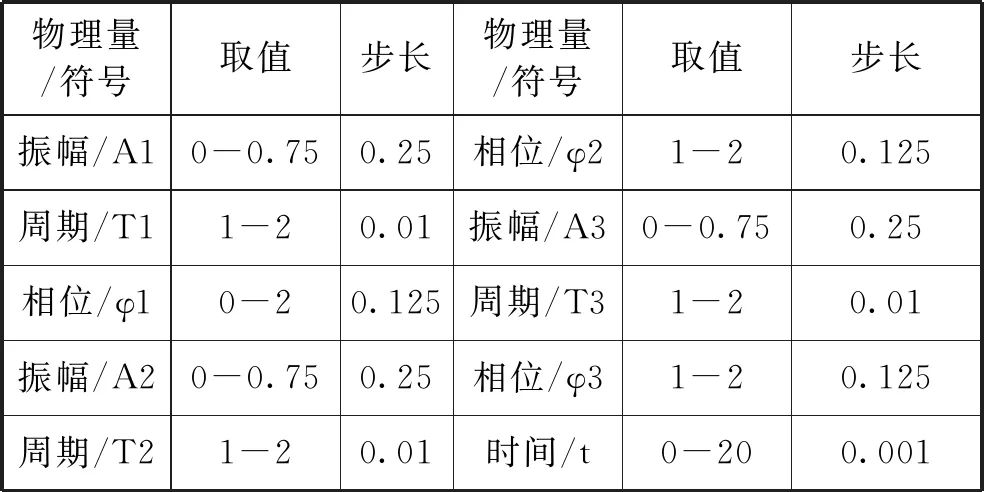
表1 振动叠加参数设定
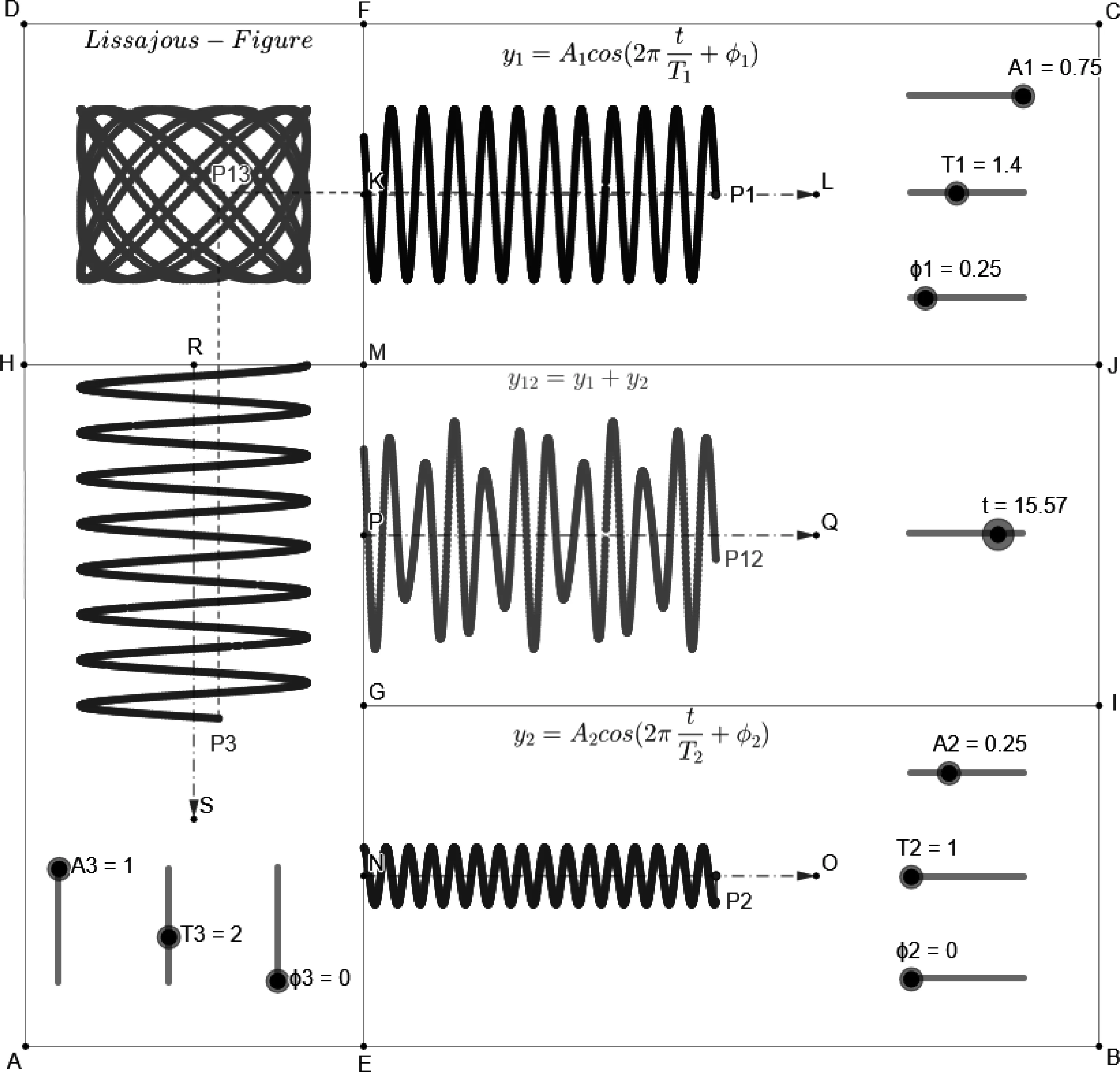
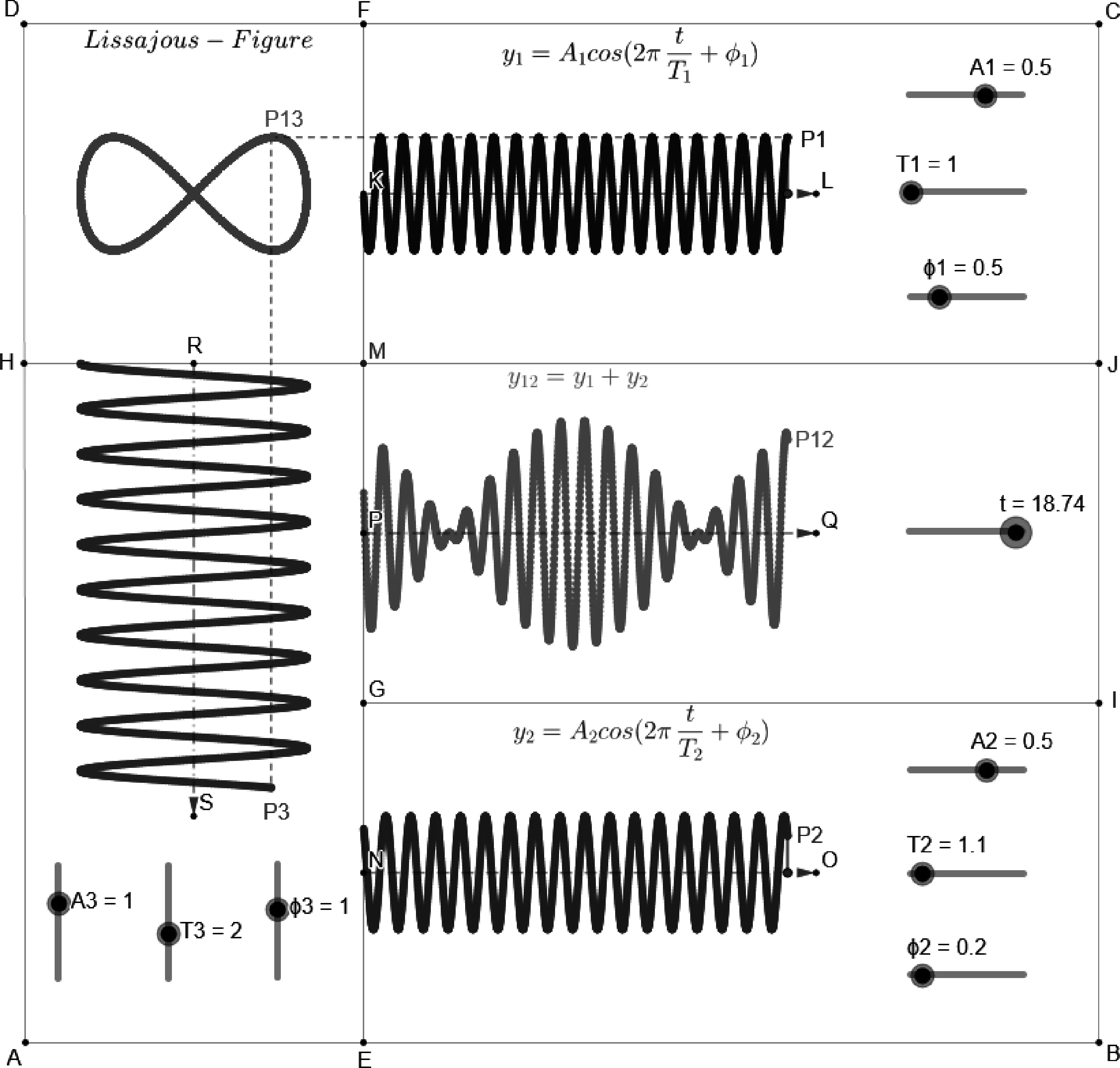
为了整齐美观,通过输入坐标,如A=(0,0),B=(9,0),C=(9,9),G=(3,3)等,建立A~S等坐标点,用线段连接两点进行分区显示. 振动曲线的横轴显示范围为3-7,而时间t的取值范围为0-20,因此振动点在t时刻的横坐标可以表示为3+t/5. 输入P1=(3+t/5, A1*cos(2*pi*t/T1+φ1*pi)+7.5)建立第1个坐标随时间t做简谐运动的点. 同理建立参与叠加的第2个简谐运动点P2=(3+t/5, A2*cos(2*pi*t/T2+φ2*pi)+1.5). 合振动则由P12表示,P12=(3+t/5, A1*cos(2*pi*t/T1+φ1*pi)+A2*cos(2*pi*t/T2+φ2*pi)+4.5). 对于垂直振动的第3个简谐运动,输入P3=(A3*cos(2*pi*t/T3+φ3*pi)+1.5, 6-t/5). 当考虑P1和P3两个相互垂直的简谐运动叠加时,建立点P13.该点在任意时刻的纵坐标为P1在该时刻的纵坐标,而横坐标为P3点在该时刻的横坐标,所以输入P13=(x(P3),y(P1))建立合振动点. 为了显示振动轨迹,P1,P2,P3,P12,P13共5个点均需在右键菜单中勾选“显示踪迹”. 至此,一副能够同时演示平行及垂直简谐运动叠加的全参数可调的动态演示图就绘制完毕. 附录中图1为同频率平行振动叠加及周期比为3∶4,相位差为0.5π的李萨如图形演示结果. 附录中图2为不同频率平行振动叠加及周期比为7∶10,相位差为0.25π的李萨如图形演示结果.可见当两个平行振动频率不同时叠加结果就不是简谐运动了.根据理论可知,如果两平行振动的振动频率很大但差值很小则其叠加结果出现拍现象,如附录中图3所示.可以便捷地通过参数调节详细讨论振幅、周期及相位等参数对拍现象的影响结果.[6]
2 波动的叠加动态演示
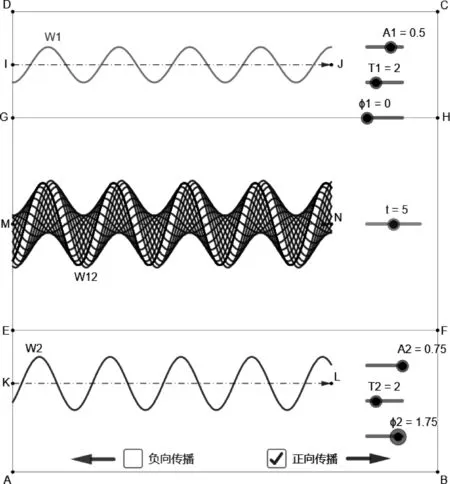
简谐波的叠加可以分为两大类,一类是同向传播的两列波的叠加,另一类是反向传播的两列波的叠加. 影响叠加结果的因素包括每列简谐波的振幅A、周期T、初相位φ及时间t,加上波的传播方向一共有8个参数,所以绘图之前先建立8个参数滑动条,如图4所示,具体参数设置见表2. 同样,为了显示整齐,先建立坐标,如A=(0,-1),B=(12,-1),C=(12,12),K=(0,1.5),E=(0,3)等,然后用线段连接两点进行分区. 输入W1=IF(0 勾选正向传播复选框,设定A1=0.75,A2=0.5,T1=T2=2,拖动φ2滑动条,改变两列波的相位差,对应的叠加波的变化轨迹如附录中图4所示. 相似的,可以通过调节任一参数对简谐波的叠加结果进行动态观察,真正实现了波动叠加的全参数可调动态演示. 如果取消勾选正向传播,而勾选反向传播复选框,设定A1=0.5,A2=0.5,T1=T2=2,φ1=0,φ2=0.75,满足频率(周期)相同、振幅相同、波速相同、振动方向相同、传播方向相反的驻波条件,改变时间参数t即可得到驻波的叠加结果,如附录中图5所示,可以观察到明显驻波特征——波节和波腹. 一般学生容易觉得振幅相同不是形成驻波的必要条件,其实这种臆想很容易就可以通过演示来进行证伪,振幅不同时,叠加波的波形是不能“驻”下来的. 绘制过程简单的一副GeoGebra波动叠加图演示起来直观、生动,并且可以对波的叠加问题做到全参数可调,不仅能够有效的加深学生印象,而且给学生全面探索波动叠加问题提供了一种简单易行的方式. 表2 波动叠加参数设定 本文针对简谐运动和简谐波的叠加这两个相关物理教学内容,采用动态数学绘图工具GeoGebra进行了全参数可调的动态绘图 演示,使学生能够直观的观察到振幅、周期、相位差、振动方向及传播方向等物理量对叠加结果的影响,能够有效地强化学生对抽象物理知识的理解和掌握,而且也给他们提供了一种简单易用的采用动态作图方法理解抽象物理规律的可行方法. 附录 图1 同周期(T=1.5)平行振动的叠加及李萨如图形(T1∶T2=3∶4, Δφ=0.5π) 图2 不同周期平行振动的叠加及李萨如图形(T1∶T2=7∶10, Δφ=0.25π) 图3 拍现象及李萨如图形(T1∶T2=1∶2, Δφ=0.5π) 图4 同向传播两列波相位差对叠加结果的影响 图5 同频率同相位同振幅反向传播两列波形成的驻波演示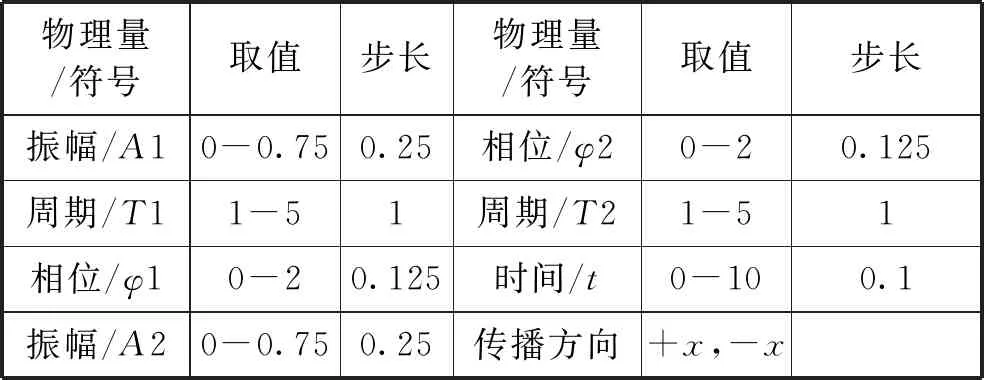
3 小结