“向量法解决直线与平面所成角问题”的教学与思考

李琳

立体几何模块是高中阶段学习的重点，学生在《数学必修2》的学习基础上，结合空间向量又在选修2-1中补充学习，这不是简单的重复学习，而是从新的视角对空间图形的位置关系与度量问题进行学习，而且为解决立体几何中某些用综合法解题时技巧性较大、随机性较强的问题提供了一些通法，从而进一步提升学生的空间想象能力和几何直观能力.教师在教学过程中如何做到既注重基础知识的教学，又能拓展学生的思维进而达到培养学生能力的目的？下面笔者以“向量法解决直线与平面所成角问题”的教学为例展开论述.

一、教学设计

（一）课前导入有的放矢

由于本节课不是概念课，也不是新授课，师生已经对教材（人教A版选修2-1）《立体几何中的向量方法》进行了学习，对空间向量这个工具的使用有了一定的基础和认识，所以笔者设计了以下三道小题给学生课前完成：

1.已知空间向量a=（1，1，0），b=（x，-1，1），若〈a，b〉=π3，则x=（）.

A.0或4

B.0

C.4

D.1

2.已知A（3，-1，4），B（2，1，3），若AP=λAB，则P点的坐标是（）.

A.（3-λ，2λ-1，4-λ）

B.（λ，λ-1，2λ）

C.（λ，2λ，2-λ）

D.（3λ，2-λ，λ，）

3.如图1所示，在棱长为4的正方体中，点P在B′C′上，且C′P=14C′B′，则直线PA与平面ABCD所成角的余弦值为.

图1

习题1的设计是检测学生向量夹角公式的掌握情况，结果绝大部分学生错选成了A，究其原因是学生忽视了向量夹角的范围，未注意到在计算过程中对方程两边平方会扩大变量的范围.如果学生在求解过程中列出了式子：12=x-12x2+2，注意到向量夹角为锐角时其数量积为正数，就可得出x>1，可以选出正确答案C;习题2的设计是为后面例题1的变式做铺垫的，检测的知识点是向量共线的应用，答题效果比较好.习题3的设计是借助一个正方体求直线与平面所成角的余弦值，这里有两个设计意图：其一是此题用向量法和综合法都很容易入手，学生可以自由选择方法，其二是题目求的是直线与平面所成角的余弦值，若学生用向量法解题的话这里是个易错点，不少学生对向量法求出的值到底是正弦值还是余弦值还有些混淆.因此，本节课的课前导入就是通过习题帮助学生查缺补漏，并围绕本节课的教学重点进行归纳小结，让学生明晰知识点、明确考点，学习过程中做到心中有数.

（二）課中题型精选典型

数学教学离不开解题教学，解题教学的首要工作就是精选例题.高中阶段的数学学习更多的是通过培养学生的思维品质，达到提升学生学习能力的目的，因此，教师选取的例题需有基础性、典型性和示范性的特征.笔者选取了如下题作为课堂例题：

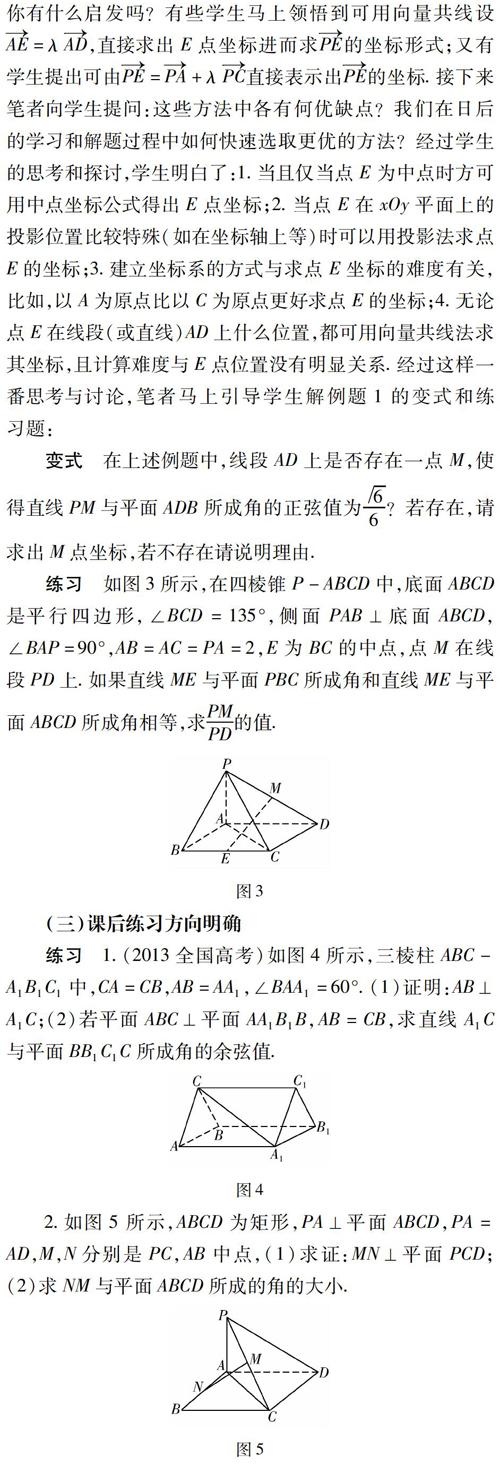
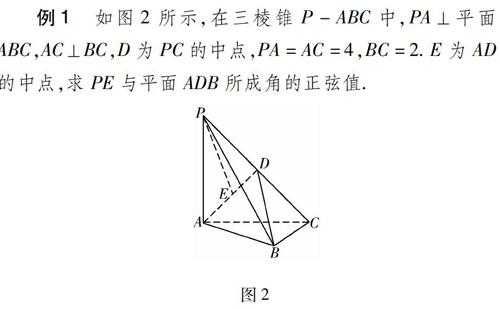
例1 如图2所示，在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，D为PC的中点，PA=AC=4，BC=2.E为AD的中点，求PE与平面ADB所成角的正弦值.

图2

用向量法求直线与平面所成角本身难度不大，学生的难点主要集中在建立空间直角坐标系和找空间点的坐标这两项.笔者选取的这道例题无论是建系还是找点的坐标学生都很容易入手，题目比较基础，解答方法也有典型示范的功能.设计意图是强化用向量法求直线与平面所成角的“三步曲”：化为向量问题——进行向量运算——回到图形问题.第一步是向学生渗透化归与转化的思想，第二步考查学生的运算能力和综合能力，第三步强化学生对知识的理解和掌握.为了拓展学生的思维，例题讲完后笔者设计了一道探究题：你还有哪些方法得出E点的坐标？由于学生最容易想到直接求E点坐标，所以容易想到的方法有：用中点坐标公式求的;先找E点在底面投影再求E点坐标的;这时笔者提示学生：根据A，E，D三点共线及课前演练的第二小题，你有什么启发吗？有些学生马上领悟到可用向量共线设AE=λAD，直接求出E点坐标进而求PE的坐标形式;又有学生提出可由PE=PA+λPC直接表示出PE的坐标.接下来笔者向学生提问：这些方法中各有何优缺点？我们在日后的学习和解题过程中如何快速选取更优的方法？经过学生的思考和探讨，学生明白了：1.当且仅当点E为中点时方可用中点坐标公式得出E点坐标;2.当点E在xOy平面上的投影位置比较特殊（如在坐标轴上等）时可以用投影法求点E的坐标;3.建立坐标系的方式与求点E坐标的难度有关，比如，以A为原点比以C为原点更好求点E的坐标;4.无论点E在线段（或直线）AD上什么位置，都可用向量共线法求其坐标，且计算难度与E点位置没有明显关系.经过这样一番思考与讨论，笔者马上引导学生解例题1的变式和练习题：

变式 在上述例题中，线段AD上是否存在一点M，使得直线PM与平面ADB所成角的正弦值为66？若存在，请求出M点坐标，若不存在请说明理由.

练习 如图3所示，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠BCD=135°，侧面PAB⊥底面ABCD，∠BAP=90°，AB=AC=PA=2，E为BC的中点，点M在线段PD上.如果直线ME与平面PBC所成角和直线ME与平面ABCD所成角相等，求PMPD的值.

图3

（三）课后练习方向明确

练习 1.（2013全国高考）如图4所示，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°.（1）证明：AB⊥A1C;（2）若平面ABC⊥平面AA1B1B，AB=CB，求直线A1C与平面BB1C1C所成角的余弦值.

图4

2.如图5所示，ABCD为矩形，PA⊥平面ABCD，PA=AD，M，N分别是PC，AB中点，（1）求证：MN⊥平面PCD;（2）求NM与平面ABCD所成的角的大小.

图5

围绕本节课的教学重点笔者设计了两道解答题作为课后练习.两道练习题难度均不大，其中第1题是2013年的全国高考题，学生掌握了用向量求线面角的方法就可以建立空间直角坐标系解答，大部分学生采用了此法，另外也让学生了解了这个知识点在高考中的重要性和考试的难易程度.第2题两种常用的解法向量法和综合法都容易入手.

由于本节课的重点是向量法解决直线与平面所成角问题，通过已有的学习学生对向量法解决立体几何问题有了一些基本的认识和方法，再加上前面有例题1和探究思考的铺垫，所以变式和习题都能解答出来，最后师生共同小结本节课的学习内容和重难点问题.

二、教学思考

（一）例题、习题选取要有目的性和典型性.

由于高中数学知识点多、又有一定的抽象性、综合性和难度，再加上高中生的学习任务又重，这就要求教师在备课时对例题和习题要精心选取，围绕本节课的教学内容、教学内容在教材中的地位和知识体系中的作用以及学生的学习情况等诸多因素有目的地选取一些典型的题目.一题多解和一题多变可以实现这一目标.比如，前面教学设计中选取的例题，结合马上要处理的二面角问题可以变为：线段AD上是否存在一点M，使得平面PMB与平面ADB所成角的余弦值为66？若存在请求出M点坐标，若不存在请说明理由.有了前面求线面角的铺垫，学生很快能找出解题思路和方法.

（二）数学学习过程是数学知识的“再发现”过程

数学学习过程是一個知识的“发现”过程.知识的“再发现”是从观察、分析和概括具体事例开始的.由于认知水平的限制，学生不可能独立地完成“再发现”过程，而必须通过教师的启发引导.因此，在本节课的教学中笔者设计了一个思考题：你是怎么求点E的坐标的？还有其他方法吗？让学生通过对点E的位置和不同建系的方式的观察，去分析和思考有哪些途径和方法可以找出E点的坐标，最后对各种方法进行比较归纳，概括出具体的结论.从而为“再发现”创造条件.以后学生再遇到找空间点的坐标时就有了“捷径”可走，可以降低解题难度，也可以减少解题过程中的弯路.

另外在实施教学过程中，教师讲完例题后总结用向量法的“三步曲”：化为向量问题——进行向量运算——回到图形问题，实际是让学生经历从具体事例中概括出数学理论，完成从具体到抽象的过程，再通过变式和习题的练习实现从抽象到具体，从而达到巩固所学知识的目的.具体——抽象——具体是数学教学的显著特点，也是数学教学的基本形式.