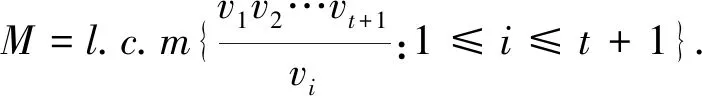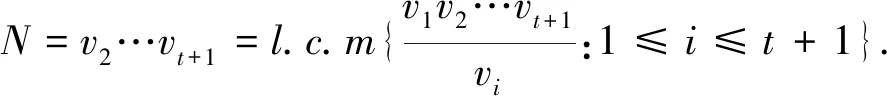一类最优混合水平定位阵*
史册, 陈光周, 曹勐
(1.上海立信会计金融学院 统计与数学学院,上海 201209;2.河南师范大学 数学与信息学院,河南 新乡 453007;3.吉林大学 数学学院,吉林 长春 130012)
1 引 言
在基于组件的软件系统中,软件故障通常是由于组件(因子)间交互作用而产生的.软件系统可以看作一个复杂的逻辑系统,其正常工作会受到系统配置、系统内部事件及外部输入等诸多因素的影响;除此之外,这些因素之间的交互作用也可能会影响软件系统的正常运行.考虑一个具有k因素 (因子)的待测软件系统(software under test,简称SUT),这些因子分别有vi种可能的水平选择,其取值集合Vi=[0,vi-1],其中1≤i≤k. 称一个k元组(a1,a2,…,ak)(ai∈Vi,1≤i≤k)为SUT的一条测试用例(test case).相应的,称由多个这样的k元组所构成的集合为SUT的一个测试用例集(test suite).

设N,t,k均为正整数且2≤t 定义1.1一个阵列A=(aij)(i∈IN,j∈Ik)称为混合覆盖阵(mixed covering arrays,MCA),简记为MCAλ(N;t,k,(v1,v2,…,vk)),若对每个t-维交互T,|ρA(T)|≥λ.换句话说,由列i1×i2×…×it标定的N×t子阵列含Vi1×Vi2×…×Vit中每一个作为行向量的t-元组至少λ次,其中1≤i1 当λ=1,省略其下标.不失一般性,总假定2≤v1≤v2≤…≤vk. 指数型记号v1s1v2s2…vksk用来表示有si个因子其水平数为vi. 当混合覆盖阵定义中任意t列包含每个有序t元组至少λ次替换为任意t列包含每个有序t元组重复同样次数时,就给出了混合正交表定义,用MOAλ(N;t,k,(v1,v2,…,vk))[6]表示. 设混合覆盖阵MCA(N;t,k,(v1,v2,…,vk))存在,不妨设为A. 对于具有k个因素,每个因素取值为vi(1≤i≤k)的待测软件系统,按照如下方式生成一个测试用例集.A的每一个列对应这个软件系统的每一个因素,其每一个行向量对应一条测试用例.因A含有N行,故含有N条测试用例,从而形成一个测试用例集.利用混合覆盖阵作为测试用例集,其能够根据测试结果获取错误的存在与否,这是发现软件故障的重要一步,但其不能够根据测试结果准确获取具体的错误信息.从实际应用角度来看,根据测试结果能够确定出故障的具体位置是非常有意义的,因此2008年Colbourn和McClary[7]引入了定位阵(locating arrays,LA)的概念. 定义1.2[7]混合覆盖阵MCAλ(N;t,k,(v1,v2,…,vk)),A=(aij) 称为定位阵,记作(d,t)-LA(N;k,(v1,v2,…,vk)),若ρA(T1)=ρA(T2)⟺T1=T2,其中T1和T2是一个势为d的t-维交互集合. 若v1=v2=…=vk=v,(d,t)-LA(N;k,(v1,v2,…,vk))简记为(d,t)-LA(N;k,v). 定位阵数(locating array number,LAN)是定位阵(d,t)-LA(N;k,(v1,v2,…,vk))存在的最小N,用(d,t)-LAN(k,(v1,v2,…,vk))表示.若混合水平定位阵中的N=(d,t)-LAN(k,(v1,v2,…,vk)),则称之为最优的(optimal).当用(d,t)-LA(N;k,(v1,v2,…,vk))作为测试用例集时,若软件故障恰好是由d个t-维交互触发的,则这些错误均能从测试结果完全被确定出来.定位阵不但应用于定位软件系统因子交互引起的错误故障,而且还应用于度量、测试以及无线网络测试等[8-9]. 最近,TANG等人建立了(1,t)-LAN(k,v)的下界,并刻画了达到这个下界的最优定位阵的组合特征[10].但在现实生活中,软件系统的不同因子的水平取值可能是不相同的.从实际应用角度考虑,定位阵(d,t)-LA(N;k,(v1,v2,…,vk))具有更强的适用性.定位阵(d,t)-LA(N;k,(v1,v2,…,vk))还没有被系统研究.事实上,其存在的下界无从知晓.本文将研究定位阵(1,t)-LA(N;k,(v1,v2,…,vk)),其中2 称达到引理2.1的定位阵为最优的.为了描述最优混合水平定位阵的组合特性,需要给出指标两两不同的混合正交表的定义. 定义2.1设A是混合正交表MOA(N;t,k,(v1,v2,…,vk)),其中2 利用这类混合正交表可以产生如下定位阵. 定理2.1若MOA*(N;t,k,(v1,v2,…,vk))存在,其中2 证明假设A是混合正交表MOA*(N;t,k,(v1,v2,…,vk)),则对于任意两个不同t-维交互T1和T2,若T1和T2的列指标集合相同,则ρA(T1)≠ρA(T2);若T1和T2的列指标集合不同,则|ρA(T1)|≠|ρA(T2)|,进而ρA(T1)≠ρA(T2).显然,T1=T2⟹ρA(T1)=ρA(T2).因而ρA(T1)=ρA(T2)⟺T1=T2. 证毕. 证明由定理2.1知,定位阵(1,t)-LA(N;k,(v1,v2,…,vk))存在.其最优性由引理2.1得到.证毕. 本节将利用定理2.2给出若干最优定位(1,t)-LA(N;k,(v1,v2,…,vk))的存在性结果.因为在实际应用中,主要关注强度为2和3的定位阵,因此,我们给出强度为2和3的混合正交表MOA(N;t,k,(v1,v2,…,vk))的存在性结果.下文中记号l.c.m表示最小公倍数. 引理3.1[6]设2≤v1≤v2≤v3. 则 (1)MOA(N;2,2,(v1,v2))存在当且仅当v1v2|N; (2)MOA(N;2,3,(v1,v2,v3))存在当且仅当M|N,其中M=l.c.m{v1v2,v1v3,v2v3}. 引理3.2[11-12]设2 (1)MOA*(N;2,4,(v1,v2,v3,v4))存在当且仅当M1|N,其中M1=l.c.m{αβ:{α,β}⊂{v1,v2,v3,v4}}; (2)MOA*(N;2,5,(v1,v2,v3,v4,v5))存在当且仅当M2|N,其中M2=l.c.m{αβ:{α,β}⊂{v1,v2,v3,v4,v5}}; (3)MOA*(N;2,6,(v1,v2,v3,v4,v5,v6))存在当且仅当M3|N,其中M3=l.c.m{αβ:{α,β}⊂{v1,v2,v3,v4,v5,v6}}. 引理3.4[13]设2 利用定理2.2和引理3.1-3.4可以得到如下最优混合水平定位阵. 定理3.1设2 (1) (1,2)-LA(v2v3;3,(v1,v2,v3))存在,其中v2v3=l.c.m{v1v2,v1v3,v2v3}; (2) (1,2)-LA(v3v4;4,(v1,v2,v3,v4))存在,其中v3v4=l.c.m{αβ:{α,β}⊂{v1,v2,v3,v4}}; (3) (1,2)-LA(v4v5;5,(v1,v2,v3,v4,v5))存在,其中v4v5=l.c.m{αβ:{α,β}⊂{v1,v2,v3,v4,v5}}; (4) (1,2)-LA(v5v6;6,(v1,v2,v3,v4,v5,v6))存在,其中v5v6=l.c.m{αβ:{α,β}⊂{v1,v2,v3,v4,v5,v6}}. 定理3.3设22 最优性和组合刻画


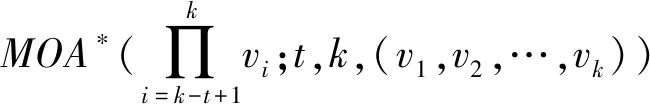
3 主要结果