观测系中伽马射线暴内光度与峰值能量关系的研究*
尹跃, 柏杨, 陈函
(六盘水师范学院 物理与电气工程学院,贵州 六盘水 553004)
1967年,一种非常奇特的天文现象被偶然发现,这种现象具有极高能、强爆发和瞬时性等特征,后来人们把这种现象称之为伽马射线暴(简称伽马暴).伽马暴的持续时间约为 0.1~1 000 s,其能段主要集中在10 KeV~1 MeV,典型光子流量约为0.01~100 cm-2·s-1[1].光变曲线和光谱形式的多样性以及极大的光度是伽马暴的最显著特征[2],任何两个伽马暴不会具有完全相同的时间结构和能谱演化过程,因此可以从伽马暴的光变曲线和能谱着手研究伽马暴理论模型和产生机制.
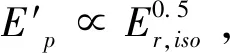
1 样本选择
以Fermi卫星从2008年6月发射到2019年1月所探测到的121个具有已知红移值的伽马暴为样本,采用RMFIT软件利用Band光子模型对这些伽马暴进行拟合.Band光子模型的经验公式为
(1)
Ec为拐折能量,其表达式为
(2)
在公式(1)中,A为振幅,α为低能谱指数,β为高能谱指数,Epeak为vFv谱的峰值能量.为了得到更加合理的样本,对由Band光子模型拟合得到的数据进行筛选,即对卡方值、高能谱指数和Epeak值的误差进行了限制,另外对每个暴的时间分辨谱的个数也进行了限制,最后选取了32个伽马暴的时间积分谱和570个伽马暴的时间分辨谱作为研究样本.
2 研究结果
2.1 伽马暴内光度Liso和峰值能量的关系

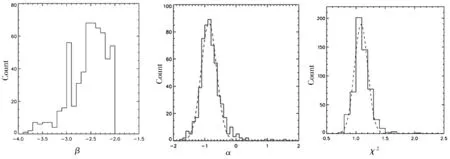
图1高能谱指数β分布图 图2高能谱指数α分布图 图3χ2柱形分布图
Fig.1Distributions of high-energy indexβFig.2Distributions of high-energy indexαFig.3Histograms for the distribution ofχ2
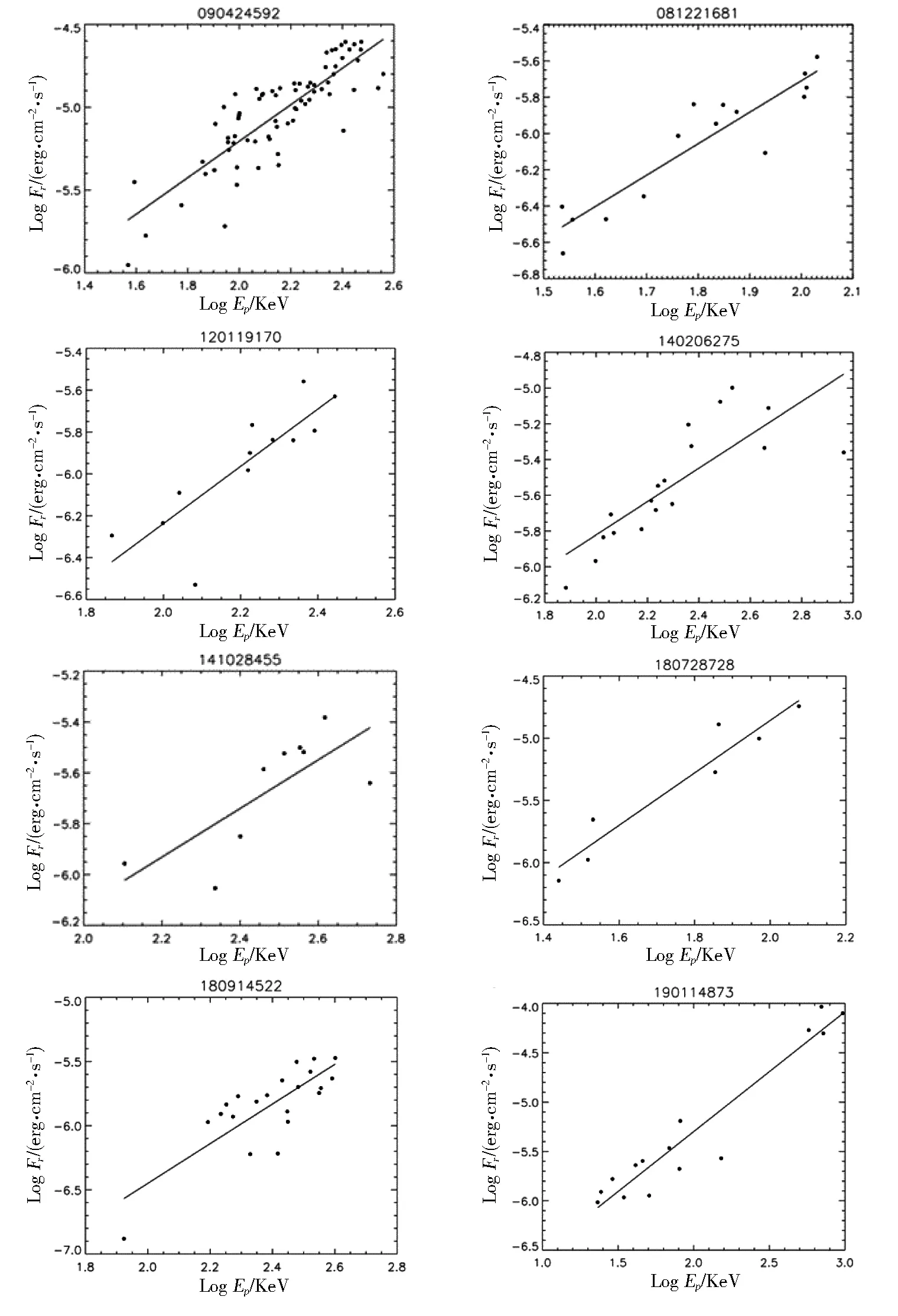
图4 伽马暴的观测流量F与峰值能量Ep的关系图
2.2 伽马暴间光度Liso和峰值能量的关系
(3)
在公式(3)中,c为光速,z为红移值,H0为哈勃常数,ΩM为宇宙的平均物质密度,ΩA为宇宙的真空能密度,这些参量的值分别取为H0=71 km·s-1·Mpc-1,ΩM=0.27,ΩA=0.73.然后用光度公式
Liso=4πdl2Fr
(4)
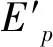



(5)

ω≈ζiR13
(6)
式(6)中,ζi是综合内激波参数;R13是火球模型的半径,其单位为1013cm.同样,从文献[9]中的(23)式,可以得出在外激波模型中,ω的表达式为:
(7)
式(7)中,ζe是综合外激波参数;σ1=σ/10,σ是冷热光度部分的比值;Γ2.5=Γ/102.5,Γ是火球的体积洛伦兹因子;E53是总能量,其单位为1053erg·s;n1是介质密度,其单位为10 cm-3.
由式(6)可知,在内激波模型中,ω的值由伽马射线发射区的半径和综合内激波参数ζi共同决定,而ζi与激波参数有关,如磁均分因子、电子分布量、电子的均分因子、电子螺距角和壳层之间的相对洛伦兹因子等,而这些参数只与碰撞壳层的物理性质有关.但对于外激波模型来说,情况比内激波模型更加复杂.从公式(7)可知,ω的值是由激波和环境参数共同决定.
计算了32个伽马暴内570个时间分辨谱所对应的ω值,然后用线性模型ω∝kt对ω的变化进行研究,k值的绝对值越大,ω值的变化越显著.ω的分布图如图7所示,从图7可以看出,其主要分布范围为0.1~1.0,k值的分布图如图8所示,其主要分布范围为-0.01~0.03.这些结果表明ω的值在不同的伽马暴以及在同一个伽马暴内部的不同时间段是不随时间变化的.如果假设在式(6)和式(7)中的参数互不相关,就可以根据ω的取值范围对这些参数进行限制.

图7 570 个能谱的ω分布图 图8 32个伽马暴的k分布图
4 讨 论


