单圈图的扩展能量的上界
2019-11-29 08:35徐幼专
山西师范大学学报(自然科学版) 2019年4期
徐幼专
邵阳广播电视大学,湖南 邵阳 422000
设G是一个简单图,顶点集为V(G)={v1,v2,…,vn}.用di表示顶点vi的度,同时, 分别用Δ、δ表示G中的最大度和最小度.G的邻接矩阵用A(G)表示,设A(G)的特征值为λi(i=1,2,…,n).因为A(G)是一个实对称矩阵,它的所有特征值都是实数,不妨设λ1≥λ2≥…≥λn,G的谱是邻接矩阵A(G)的所有特征值的集合.
在文献[12]中,Yang等引入了一个新的矩阵,称为扩展邻接矩阵,用Aex(G)=(aij)表示,其中
因为Aex(G)是实对称矩阵,它的特征值是实数,不妨设特征值为ηi(i=1,2,…,n),并且η1≥η2≥…≥ηn.
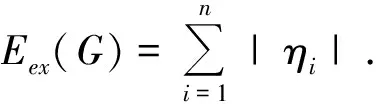
单圈图就是边数等于顶点数的简单连通图,单圈图是除树之外结构最简单的图类,它在图谱理论、复杂网络、图染色理论等都发挥着不可替代的作用.本文研究单圈图的扩展能量的上界问题.
1 主要引理
为了证明本文的定理,需要引入下列几个引理.
引理1[13]设G是一个具有n个顶点的简单图,则
引理2[15]设G是一个具有n个顶点m条边,度序列为d1,d2,…,dn的简单图,则
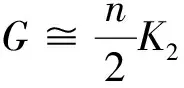
引理3[16]设G是一个具有n个顶点m条边的简单图,
(1)若2m≥n,则
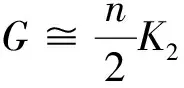
(2)若2m≤n,则E(G)≤2m,等式成立当且仅当G是边不相交的并或为孤立顶点.
引理4[17]设G是一个具有n个顶点的简单图,则
2 主要结论
现在,我们利用最大度、最小度来证明本文的结论.
定理1设G是一个具有n个顶点的单圈图,则

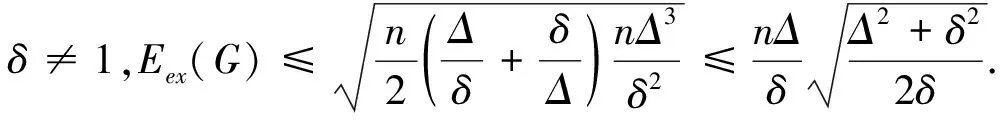


图1 具有5个顶点的单圈图
Fig.1 Unicyclic graphs with 5 vertices



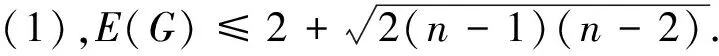

猜你喜欢
哈尔滨工业大学学报(2022年5期)2022-04-19
青海师范大学学报(自然科学版)(2021年2期)2021-12-20
烟台大学学报(自然科学与工程版)(2021年1期)2021-03-19
邵阳学院学报(自然科学版)(2019年2期)2019-05-07
福建中学数学(2018年7期)2018-12-24
中学数学研究(江西)(2018年7期)2018-07-30
发明与创新·小学生(2018年3期)2018-04-17
中学教研(数学)(2016年3期)2016-12-01
数学大王·低年级(2015年4期)2015-07-10
宜春学院学报(2015年3期)2015-01-13

