单圈图的Seidel拉普拉斯能量

周后卿，徐幼专

(1.邵阳学院 理学院，湖南 邵阳，422000；2.邵阳广播电视大学，湖南 邵阳，422000)

设G=(V，E)是一个简单的无向图，有n个顶点和m条边，顶点集V={v1，v2，…，vn}，

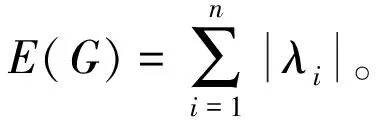
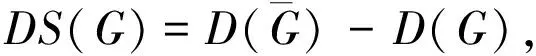
文中研究单圈图的Seidel拉普拉斯能量的界。

下面给出一些必要的定义。

定义1n阶图G叫做单圈图，如果G是连通的，并且G的边数也是n。

为了证明文中定理，需要以下引理。

引理1[10]设B=C-A，其中A，B，C均为n×n的实对称矩阵，特征值分别为α1≥α2≥…≥αn，β1≥β2≥…≥βn，γ1≥γ2≥…≥γn。则它们的特征值之间有如下关系：

下面证明Seidel拉普拉斯能量的上界。

定理1 具有n个顶点的单圈图Un的Seidel拉普拉斯能量为

(1)

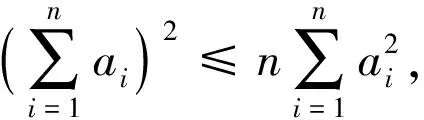
从而有

(2)

于是，

所以，根据(1)、(2)、(3)式有

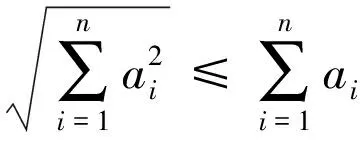
(5)

所以，由(4)、(5)式推出单圈图Un的Seidel拉普拉斯能量为