基于AVMD与极限学习机的传动箱故障诊断
赵文涛,陈雪娇,仇满意
(西安工业大学 机电工程学院,陕西 西安,710021)
传动箱的工作环境比较恶劣,因此容易出现故障,而齿轮、轴承故障又是传动箱最常见的故障,它们的好坏直接决定了传动箱运行的可靠性。当传动箱故障发生时,摩擦力的大小、外载荷的不均衡和刚度非线性等因素会引起其振动信号表现出非线性、非平稳的特征,而这些非线性、非平稳特征的振动信号中包含了丰富的力学特征,能够全面准确的反映传动箱当前的运行状态[1]。因此,对传动箱进行故障诊断,从其非平稳信号中提取它的故障特征信息,并选用合适的分类模型进行识别,就显得尤为重要。
2014年,学者DRAGOMIRETSKIY等[2]提出了一种新的用于信号处理方法——变分模态分解(variational mode decomposition,VMD)。VMD分解中,每个模态函数都有估计带宽,为了使其和最小,各本征模态函数都被解调到相对应的基频带,最后得到所有的本征模态函数和其中心频率。和传统的EMD(empirical mode decomposition )相比,VMD理论基础充实,可以通过求解变分模态的最优解来实现模态分解;与小波变换不同,它没有基函数的选取;分离信号方面,两个纯谐波,在频率接近的情况下,VMD仍能成功分离。近年来,VMD 也逐渐被用于机械的故障诊断中,在故障特征信息描述方面相对其它方法表现的更加有效[3]。但利用VMD时事先需要确定分解模态数的个数即K值,K值的大小会影响分解的精度以及效果。因此在利用VMD处理信号的时候,确定最优K值是首要解决的问题。
2006年HUANG GB等[4]提出一种新神经网络模型算法——极限学习机(extreme learning machine,ELM)。其隐层的参数不用反复调整,其网络参数的训练被转换为求解线性方程组,求得的最小二乘解为网络输出权值,训练过程一次就可以完成,缩短大量训练时间,泛化性能更为优异,识别率更高。因此,基于以上分析,文中提出基于自适应变分模态分解和极限学习机的传动箱故障诊断新方法。
1 自适应变分模态分解
1.1 变分模态分解
在VMD算法中,将本征模态函数(intrinsic modefunction,IMF)重新定义为一个调幅-调频信号,VMD分解的目的是构造并求解约束变分问题,然后将信号分解为预先设定个数的IMF分量[5]。以信号f为例,其变分过程如下,图1为VMD流程图。
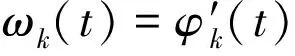
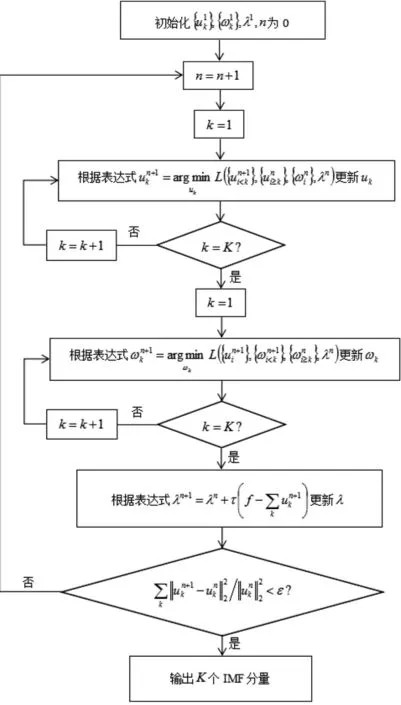
图1 VMD流程图Fig.1 The flow chart of VMD
1)利用Hilbert变换,获取各个IMF分量uk(t)的解析信号
(1)
2)为每个解析信号都估测一个中心频率ωk,利用移频把所有解析信号的频谱都转换到基带。
(2)
3)H1是频移信号的高斯平滑指标,IMF分量带宽用其来估计,得到如下
(3)
式中:{uk}={u1,…,uK}代表分解得到的K个IMF分量;{ωk}={ω1,…,ωK}表示各分量的频率中心。
求解约束变分,使用Lagrange乘子及二次罚函数项将其转换为如下无约束问题[6]。
(4)
式中:α为惩罚因子;式中λ(t)为Lagrange乘子。
无约束变分问题的鞍点用乘子交替方向算法(alternate directon method of multipliers,ADMM)求取,即公式(3)的最终解。求解约束变分问题时,各IMF分量带宽及中心频率持续变化,依据信号的原始频域特性,实现最终频带剖分,从而实现信号分解。
1.2 自适应变分模态分解
变分模态分解中事先需要确定分解模态数的个数即K值,K值的大小对分解的精度以及效果会有一定的影响[7]。因此在利用VMD处理信号的时候,确定最优K值是首要解决的问题。
为探究VMD中K对分解的影响,采用仿真信号:x(t)=x1(t)+x2(t)+x3(t),其中,x1(t)=cos4πt,x2(t)=0.25cos48πt,x3(t)=0.0625cos576πt。设定不同的K(K=2,3,4,5)值进行VMD分解,表1为不同K值分解下各模态与原信号之间的相关系数。
表1 不同K值下各模态与原信号之间的相关系数
Table 1 Correlation coefficients between each mode and original signal under different K values

ρ1ρ2ρ3ρ4ρ5K=20.991 30.363 8K=30.968 40.342 10.060 4K=40.968 40.342 10.123 70.049 6K=50.968 40.342 10.045 40.055 60.036 9
由以上分解结果表可以看出,K=4时,u4为虚假模态,u4与原信号之间的相关系数为0.049 6;同理,K=5时,u3与u5为虚假模态,其与原信号之间的相关系数分别为0.045 4,0.036 9。因此,当分解模态数K值过大时,会出现相关系数小于0.05的虚假模态。
因此,通过上述分析,提出自适应变分模态分解方法(adaptive variational mode decomposition,AVMD),在AVMD中,首先预设平衡约束参数,一般等于信号的采样频率,然后对信号进行VMD分解并计算分解后各模态与原信号之间的相关系数,设定阈值,若分解后各模态与原信号之间的相关系数最小值小于阈值a(a一般可取5%),则停止分解;反之则继续增加模态数K值,直到分解满足停止条件。见图2。
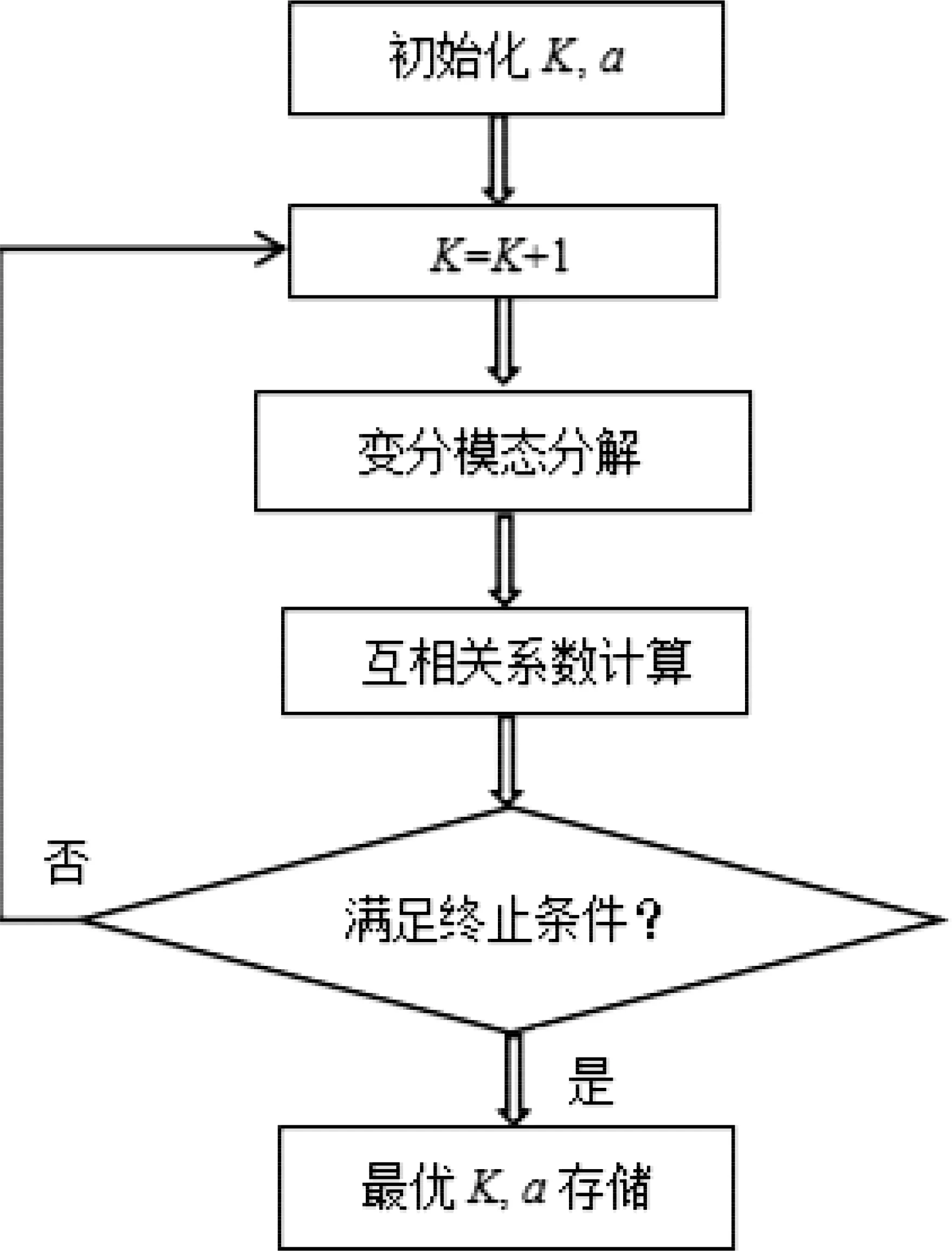
图2 自适应变分模态分解的流程图Fig.2 The flow chart of adaptive variational mode decomposition
2 极限学习机
在极限学习机算法中,假如有N个各不相同的(xi,ti)∈Rn×Rm,其中xi为一个n×1的输入向量,ti则是一个m×1的目标向量。则一个有L个隐含层节点的单层前馈神经网络(SLFN),其相应的输出表达式为
(5)
x∈Rn,ai∈Rn,βi∈Rm
式中:ai是连接第i个隐层节点和输入节点的权重;βi是连接第i个隐层节点和输出节点的权重;bi是第i个隐层节点的阈值;fL(xj)是第j个输入样本的输出值。
若以上所用这个SLFN能够在无误差的条件下逼近N个输入样本,也就是说
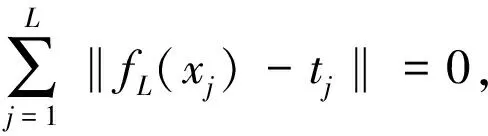
(6)
现在将式(6)合并成为矩阵格式为
Hβ=T
其中H为隐含层输出矩阵。
(7)
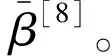
(8)
其中H+为H的Moore-Penrose 广义逆矩阵。
综上所述,极限学习机的学习过程概括如下:
1)确立前馈神经网络的具体结构。
2)对前馈神经网络的输入权值ai和隐含层节点的偏差bi,进行随机设定[9]。
3 实验研究
实验采用江苏千鹏诊断工程有限公司的QPZZ-II系统所做的传动箱故障实验数据。实验传动箱为20120607型传动齿轮箱,利用振动加速度传感器测取传动箱不同状态下的振动数据。实验平台如右图3所示。

图3 实验平台Fig.3 The experiment platform
传动箱的振动信号通过振动加速度传感器测取,其采样频率为5 120Hz,传动轴的转速为880r/min,一共采集了传动箱的4种状态(正常、大齿轮点蚀、大齿轮断齿、小齿轮磨损)下的振动数据,每种状态包含26组样本,每组样本包含2 048个数据点,共104组样本。
3.1 特征提取
首先利用自适应变分模态分解对四种状态进行分解,以大齿轮断齿为例,其分解结果如图4。为了充分挖掘特征信息,准确的反映传动箱齿轮的故障状态,需要选取合适的特征值。相比于其他特征值,奇异值特征反映了矩阵本身固有的性质,具有较好的稳定性。在机械故障诊断领域,特征矩阵往往并不是方阵,并且相同故障类型样本的特征矩阵之间差别较小,因此矩阵的奇异值可以较好的反映机械设备不同的故障状态,符合模式识别的要求[10]。故选择振动信号经过AVMD分解后的模态分量所组成的矩阵的奇异值作为故障特征,每种状态提取了26组奇异值样本,共提取104组样本。各状态相对应的类标签如下表2。
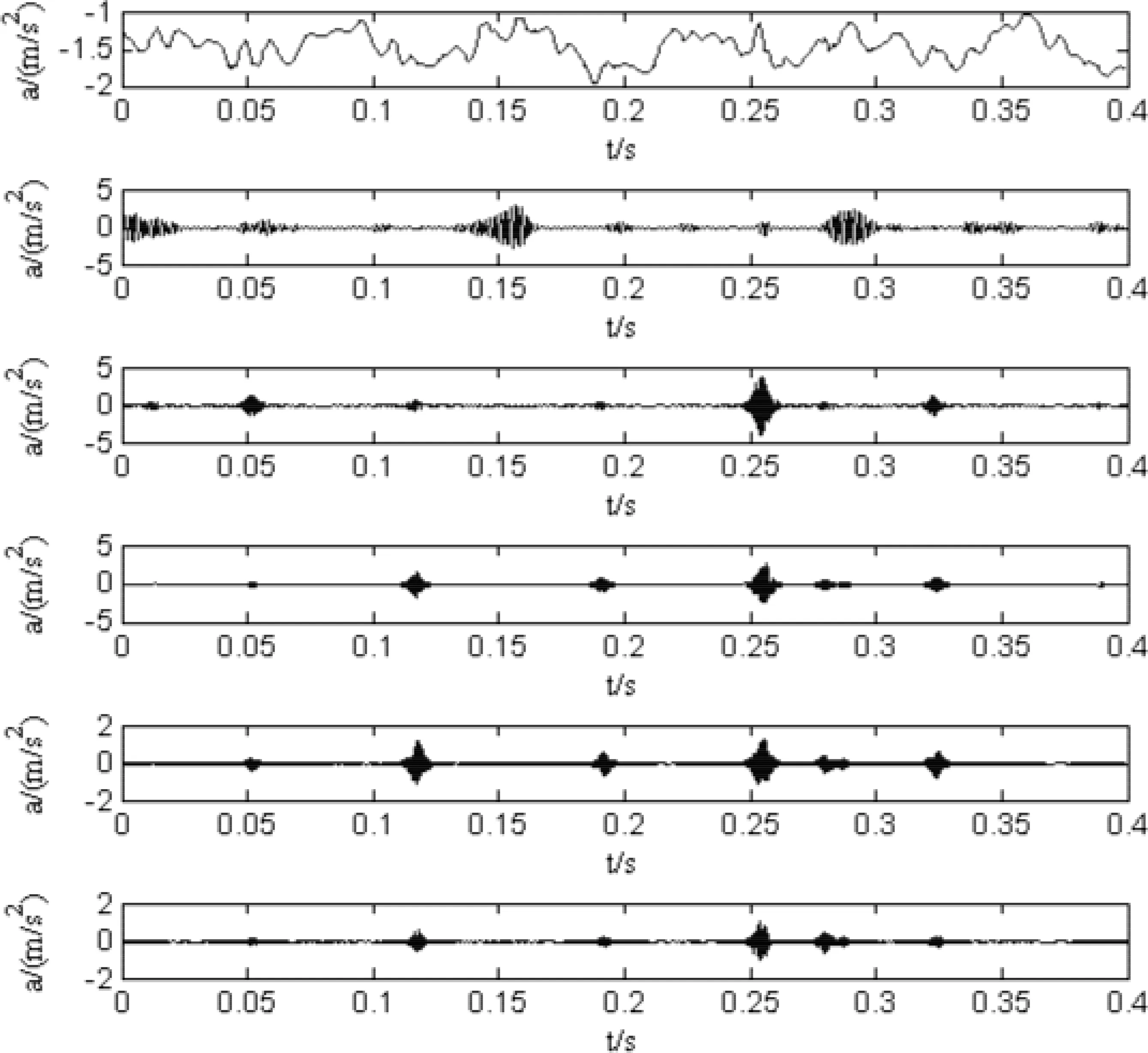
图4 大齿轮断齿状态的AVMD分解结果Fig.4 AVMD decomposition results of a bull gear in the tooth-broken state
表2 齿轮各状态的类标签
Table 2 Class label for each state of the gear

1234
3.2 故障识别
实验利用极限学习机实现故障识别,其激活函数采用Sigmoidal函数。选取特征集前52 个(每种状态13个样本)样本作为训练集,后52个(每种状态13个样本)样本作为测试集,输入到极限学习机中进行训练、测试,识别结果如图5所示。同时,由于BP神经网络是现代模式识别使用最广泛的模型,因此为了与极限学习机识别结果作对比,实验也采用了传统的BP神经网络进行故障识别,分类结果如下图6所示,下表3为二者诊断性能表。图中实际分类用“*”表示,分类器的分类用“。”表示。二者发生重叠,表示分类是正确的,否则分类错误。
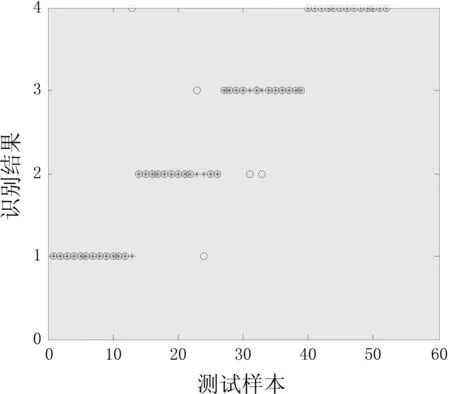
图5 极限学习机识别Fig.5 Identification of ELM
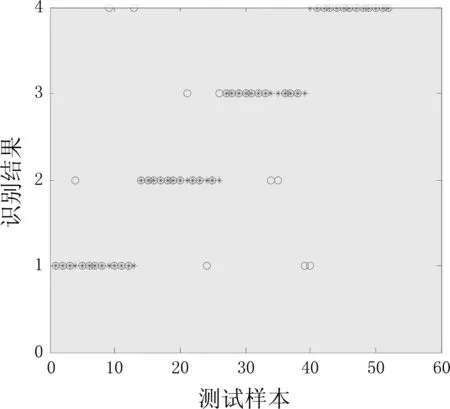
图6 BP神经网络识别Fig.6 Identification of BP neural network
表3 分类器诊断性能表
Table 3 Diagnostic performance table ofa classifier

/%/s90.40.676 3BP80.810.274 3
3.3 结果分析
由以上两种诊断模型的测试识别结果可知,基于AVMD和极限学习机的识别率高于基于AVMD和BP神经网络的识别率,同时前者的故障识别时间远远小于后者。这是因为在训练过程中,极限学习机的输入权值和偏差不需要不断调整,利用随机设定的输入权值和偏差就可以对结果进行调整,因而计算复杂程度低,运算速度快。同时求解最小二乘范数解的过程是一个凸优化过程,局部最优不易发生。缩短了大量训练时间,泛化性能更优良,拥有更高的识别率。
4 结论
全文提出了一种基于AVMD和极限学习机的传动箱故障诊断方法。通过传动箱大齿轮点蚀、大齿轮断齿、小齿轮磨损、正常这4种工况信号的识别实验,验证了文中提出的故障诊断方法的有效性。相比于基于AVMD和BP神经网络的方法,文中提出的方法具有更高的识别率和识别速度,进一步说明了基于AVMD和极限学习机的新方法的优越性。同时,其对于实际工业设备状态监测也具有一定的指导意义,也为机械故障诊断提供了一种新思路。

