适用于低空舰载导弹隐蔽航路规划与匹配定位的海图构建

(1. 海军大连舰艇学院 军事海洋与测绘系，辽宁 大连 116018；2. 海军大连舰艇学院 导弹与舰炮系，辽宁 大连 116018)

低空舰载导弹借助相关地理信息规划航路，有助于导弹以低速(亚音速)的方式隐蔽地深入敌区进行突然打击，从而实现提升航路质量、达成战术意图的目的[1]。导弹在飞行的同时要顾及定位的准确性，才能够及时调整航路。通常，惯性定位系统的误差易积累，卫星定位易遭攻击且稳定性差，而使用匹配定位能够避免这些缺陷。此外，由于导弹从海面发射，故其航路和定位的配套测绘保障离不开现有海图的支持。

为了建立航路规划和匹配定位在海图中的联系，需要寻找连续的可匹配定位区域。首先，由于岛屿边界、沿岸的地理信息变化较为明显，是理想的匹配定位区域。其次，在这些可匹配区域飞行的导弹由于地物多路径干涉效应[2-3]的影响较难被雷达捕获，导弹的隐蔽性得到了提高。为了进一步处理岛屿边界、沿岸的可匹配区域，需要将其进行网格化。文献[4]提出利用等间距平行线的方法来自动进行矢量结构向网格结构转换，在一定程度上解决了矢栅转换的效率问题，但得到的规则网格数据量较大，而通过应用四叉树算法得到网格地图可以减小数据存储。在网格地图的路径规划问题上，文献[5]提出了四叉树算法处理后网格地图的路径规划，但由于该方法未被进一步应用在真实地图数据中，所以未能分析网格化的限制条件及验证规划路径的适用性。

本研究在矢量海图的基础上，提出一种海图构建方法以满足航路规划与匹配定位的用图需求。对比不同精度指标的海图处理算法，尽可能精细化、合理化表达海图。在规划航路方面兼顾隐蔽性，利用智能算法规划顾及岛屿沿岸的隐蔽航路。在大部分岛屿沿岸的可匹配定位区域，依据文献[6]提出的利用激光探测技术实现海底地形辅助匹配导航定位的方法，可在海陆交接的浅水区实现浅水深点的辅助匹配定位。这样规划的航路在可匹配定位区域上空，可以极大程度地扩充用来进行匹配定位特征区域的范围，并且在辅助惯性导航系统定位的基础上实现航路的规划。同时低空沿岸飞行的导弹可以充分利用多路径效应，特别是这种效应在海陆交接区域对雷达探测产生杂波信号的作用，来实现规划躲避敌方雷达探测、捕获的隐蔽性航路。

1 海图构建及航路规划定位算法

1.1 适用于低空导弹海图的特点

低空导弹所使用的海图，需要保障其规划航路的隐蔽性和定位的准确性。在导航定位方面，排除惯性定位和卫星定位，匹配定位无疑是最佳的。只要存在可匹配区域，则导弹的定位精度就能够得到一定程度的保障[6]。由于低空导弹飞行时距离海面、陆地的垂直高度较近，地物、海面的多路径干涉效应[3]明显，同时也意味着较难被敌方雷达捕获。

虽然导弹低空纵深航行于陆地间需要大量地形数据的保障，同时也极容易因为不能及时避障而坠毁，但导弹在沿岸巡航的航路避障的困难程度得到减轻，又能够借助海陆交接的多路径效应降低敌方雷达的捕获概率，所以这样的航路具有隐蔽性。

此外，由于海图不同于陆地地图，在原有海图的表示中，陆地部分并不详细，仅突出了局部高程、等高线等有助航性质的地图要素，而对于地形地貌的表述往往是概略性的。在此基础上，低空导弹要利用海图的陆地部分进行航路规划和匹配定位将会带来较大的误差。但是海图对于岛屿、岸线的描述尤其是基岩海岸线的呈现较为清晰[7]，同时轮廓线的变化形态也有助于匹配导航定位的实施。

以岛屿岸线轮廓为基础数据构建的海图，避免了低空导弹经过复杂地形地貌时的三维航路规划以及三维避障处理的情形，转而用固定的巡航高度进行二维平面的航路规划，同时地物效应的影响增强了导弹的隐蔽性，也减轻了测绘数据保障的复杂度，减小了碰撞概率。综上所述，在原有海图的基础上，通过岛屿、岸线轮廓的表达呈现适用于低空导弹飞行用的专题海图，不仅能够使导弹规划的航路具有隐蔽性，同时也有利于导弹进行匹配导航定位。

1.2 四叉树算法构建网格化海图

1.2.1 算法原理

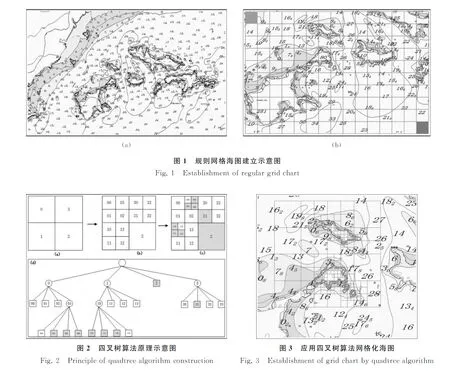
潮汐规律对岛屿、海岸轮廓线的影响不是本研究的重点，故需要重新构建处理的电子海图中的岸线轮廓可以认为是某一时刻的岸线轮廓。依据现有矢量形式的电子海图，在提取岸线轮廓前需要对原有矢量海图的精度即比例尺大小进行说明。一般情况下用来匹配定位的地图比例尺在1∶50 000至1∶100 000之间，实际应用中根据具体应用场景并结合航路规划用图的特点选择相应比例尺的矢量地图，再进一步进行规则网格化的划分，如图1所示。通常，单位网格的数值是依照“点栅格”的方式进行描述的，即网格中心点不单单是该网格区域的高程平均值，也可以是平均水深值[8]，在海陆交接处的网格单元需要采用更为合理的面积占比原则进行取值。在规则网格海图的基础上，应用四叉树算法进一步离散化分割海图，可以有效减少存储空间、提高效率，并且经过处理后的岸线、岛屿边界等沿岸地形能够被尽可能地精细化表达。

网格海图是基于四叉树算法原理建立的。在航路规划的网格地图中，单位网格分为可行、禁行状态。如图2所示，在四叉树中，每棵树由4个节点组成。每个节点树用方框、圆来表示，实心方框节点表示该区域处于禁行状态，空心方框节点表示该区域处于可行状态，空心圆节点表示该区域可以继续划分。应用四叉树算法的网格海图的表示效率要高于规则网格地图[8]，图中规则网格地图需要8×8=64个存储空间，而应用四叉树算法仅需要19个存储空间。利用四叉树算法原理将相关岛礁区中岛屿边界进行网格化(图3所示)，能够加快计算机处理数据的速度，在一定程度上有助于导弹规划定位系统响应速度的提高。

1.2.2 应用四叉树算法网格化海图的限制条件

针对某比例尺矢量海图中的岛屿沿岸边界，应用四叉树算法进行网格划分，使得边界能够被精细化表达[9]。上述过程中，应用四叉树算法划分的网格较密，则计算量较大或者过于满足匹配定位的要求，若网格划分较疏或者出现局部划分不精细的现象，则会影响航路规划与匹配定位的进行，因此需要对网格划分的限制条件进行确定。

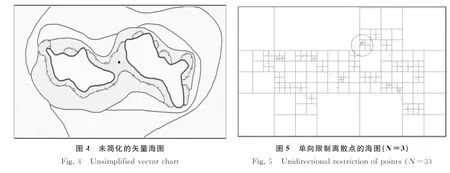
对矢量海图的处理主要分为提取边界点和边界线两种方法。在海图比例尺满足匹配定位的前提下，提取图4所示矢量海图的岛屿边界和原有海图数据中组成轮廓线的离散点，应用四叉树算法时分别依据不同限制条件进行网格划分[10-11]。在四叉树算法划分中，划分的最小网格称为“顶层网格”，顶层网格个数越少，航路规划时需要局部处理的航路段就会增加，则说明划分的限制条件缺乏适用性；顶层网格个数越多，则划分的层数随之增加，说明划分的过于精细降低了算法的效率、增加了用来规划和定位的用时。为了进一步说明海图构建的合理性，结合表1和图5～7中矢量海图不同限制条件的划分效果进行阐述。

当限制每个最小网格中至多有N个离散点，即单向限制离散点时。如表1所示，N=1时，顶层网格个数等同于离散点的个数且划分层数过多，过于满足匹配定位要求、导致计算量增加；增加N的值会出现少量的顶层网格，不利于匹配定位的进行。图5所示为限制每个最小网格中至多有3个离散点时的划分效果，圆形区域所示的顶层网格数量过少。此外，圆形区域内离散化的标准无法做到完全的一致，出现表达过于精细或者过于粗糙的现象，这样就会使得匹配定位区域的匹配相关性具有一定的复杂度，从而影响匹配定位与规划航路的生成效率。

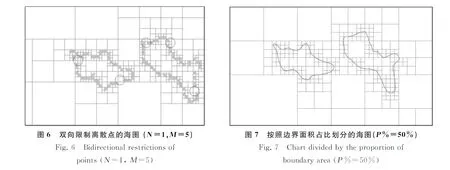
当限制每个最小网格中至少有N个离散点以及最大划分层数为M层时，即双向限制离散点时。表1所示双向限制离散点中顶层网格的个数明显优于单向限制离散点，但会出现局部划分过疏或过密的不合理情形。以N=1，M=5为例，图6所示海图中大部分边界表达较为精细，但出现了圆形区域网格划分较为疏散的情形。

表1 具体精度参数分析数据

将岛屿轮廓线与当前网格相交的面积占比P%作为网格划分的依据，岛屿作为被裁剪的多边形，裁剪窗口为正方形网格，得到一个新的多边形，其面积在当前网格的占比超过P%时，需要继续剪裁，反之停止。为了避免出现网格过大而停止划分的情况，还需限定当前网格相交所占最大面积为固定值S0，不满足则继续划分。表1所示在三种不同面积比例下，与上述两种限制条件相比，顶层网格个数适中、划分的层数也比较稳定。图7所示是依据面积占比P%=50%时的网格划分海图，这种划分方式的网格划分层数较为合理，没有出现零散顶层网格的现象，十分有利于匹配定位和规划航路相关算法的应用。

1.2.3 构建海图的精度评价

在构建面向航路规划与匹配定位的自适应网格海图时，需要控制好，使构建的海图模型与真实的海岸、岛礁、浅水深海底区域之间的整体差异性最小，从而满足海图模型的精度要求。通常，这种差异性是用构建海图与真实数据之间的中误差δh来描述。由于本文海图模型的构建是在轮廓线的基础上应用四叉树算法的网格划分，则需要获取n个落入最小网格中的高程值或浅水深值h′i，用h表示该网格所代表的高程值或浅水深值，则该网格的中误差的计算公式如下：

(1)

由于原海图的比例尺需要满足1∶50 000至1∶100 000才能够进行匹配定位，设比例尺的分母为M、构建海图的单位网格的边长为l。则l·M代表真实地图的长度，同时也反映了构建海图的量测精度，即构建网格海图的比例尺为1∶(l·M)，需要在1∶50 000至1∶100 000的范围内方能符合匹配定位要求。

1.3 航路规划与定位算法

在四叉树算法构建海图的基础上，利用蚁群智能优化算法[12]规划隐蔽性航路，充分发挥蚁群算法并行性强的特点，得到规划航路的满意解。同时构建的海图也能够保障利用激光测高、测距的匹配定位。

1.3.1 基于沿岸约束条件的蚁群规划算法

应用蚁群算法时，航路i的约束条件用θi(0<θi<1)表示，θi=0表示禁止航行，蚂蚁选择其他网格。用γn表示航路经过第n个岛屿沿岸的权重值，与信息素和启发信息相对权重参数的α、β的关系式为αn+βn+γn=1，算法中标签为k(k=1,2,…)时蚂蚁的状态[13]，在时间t时刻，能够发生从i到j节点的概率事件表达式为：

(2)

其中τij(t)表示t时信息素余量，allowedk={1,2,…}-tabuk表示蚂蚁k下次选择的节点，tabuk是存储已知节点，ηij表示节点间的期望。

在tn周期中，蚁群算法信息素更新公式：

(3)

式(3)中，信息素增量用Δτ表示，信息残留取值为ρ∈(0,1)，解算后得到公式(4)，其中Q为信息素强度。

(4)

1.3.2 基于激光测深、测高的匹配定位手段

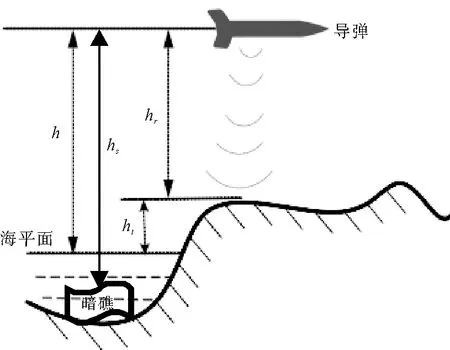
图8 匹配原理示意图

图8所示，地形轮廓匹配(terrain contour matching，TERCOM)算法是通过导弹上的激光测深、测高系统[6,14]来实时获取高程点值hr以及浅水区中水深点(浅水深点的最大值设定需要依据激光器自身性能判定)的相对高度hs。此时绝对高度h为实测值，h与hr或是hs相减得高程差值或水深值。通过惯性定位的位置信息和四叉树网格构建的海图数据库，计算高程hm以及相关极值点对应的位置就是导弹的飞行位置。同样，在浅水区测量t+i时刻的ht+i和t时刻的ht对照存储值计算出差值为：Δh=ht+i-ht。

通过采集实测某段序列的路径，并与导弹匹配系统中存储的平行该段路径的序列进行比对判断，其中指标的选定主要有三种：JCOR交叉相关值(cross correlation, COR)、JMAD平均绝对差(mean absolute difference, MAD)和JMSD均方差(mean square difference, MSD)算法，公式分别定义为：

(5)

(6)

(7)

式(5)、(6)、(7)中，hm、hr/s、Δe、Δn分别表示存储的序列值、实测的序列值和在该方向上的偏移量。由文献[15]对精度的比对可知，均方差JMSD较为合适。

1.4 海图构建流程

通过海图构建及航路规划定位算法的分析描述，给出所提海图构建方法的伪代码(表2)，以及适用于航路规划与匹配定位的海图构建算法流程图(图9)。

表2 应用四叉树算法网格化海图伪代码

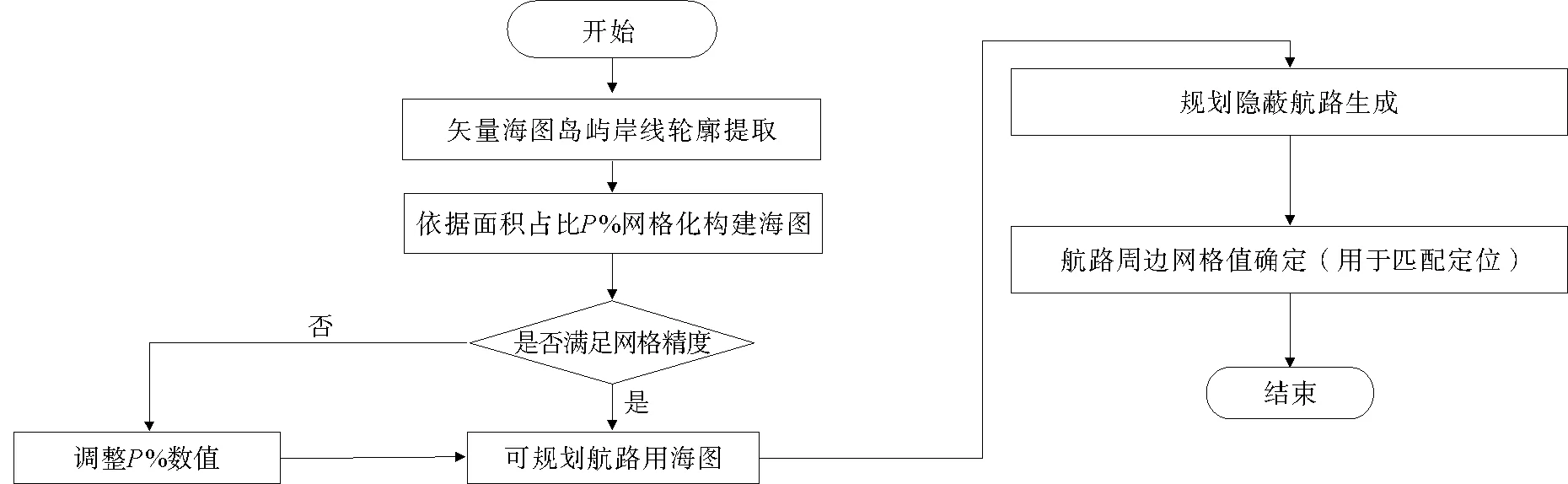
图9 适用于航路规划与匹配定位的海图构建算法流程图

2 仿真实验

2.1 适用于航路规划与匹配定位的海图仿真

应用上一节所提方法，在提取的矢量海图岛屿轮廓线的基础上，构建出应用四叉树算法满足匹配定位要求的网格海图。在构建过程中，网格所代表的高程值或浅水深值是在该网格中误差极小值情况下选取的数值。

图10 四叉树算法划分的海图中网格值的确定

图10所示四叉树算法划分的海图中网格值的确定，即落入h′所在网格的四个点为h′1、h′2、h′3、h′4，得到网格的中误差δh：

(8)

使得δh最小，则得到h′的值，按照该方法整理所划分的网格，网格的水深、高程数值如图11所示。为说明海图在匹配定位方面的适用性，图11在生成隐蔽性导弹航路的基础上应用TERCOM匹配算法。设置低空导弹垂直于海平面飞行实时高度测值为80 m，则第1组数据：实时高度为86、90、90、94、82 m，待匹配网格数值为-6、-10、-10、-14、-2 m；第2组数据：实时高度为76、75、65、67、74 m，待匹配网格数值为-4、-5、-15、-13、-6 m。匹配结果见表3，可知通过匹配定位，求得的MSD最小值为实际的导弹飞行路径，即两组匹配的方向分别为由西至东和由西北至东南两个方向。对于匹配仿真需要补充说明的是，由于附加沿岸约束条件的航路规划，可以在导弹航行过程中提供较为丰富的匹配特征点，而对于是否满足合理的特征点个数关系到识别海图的时效性和精确性。为此，如果匹配效果不理想，需要将基于激光测深、测高的匹配定位仿真结果反馈到规划航路中，从而对航路附加约束条件相关权重进行调整(主要调整的是航路与轮廓线的距离和形状相对一致性)，能够在一定程度上保证构建海图的容错性。

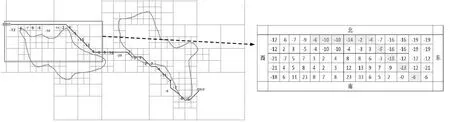
图11 四叉树算法划分的网格海图用于匹配定位

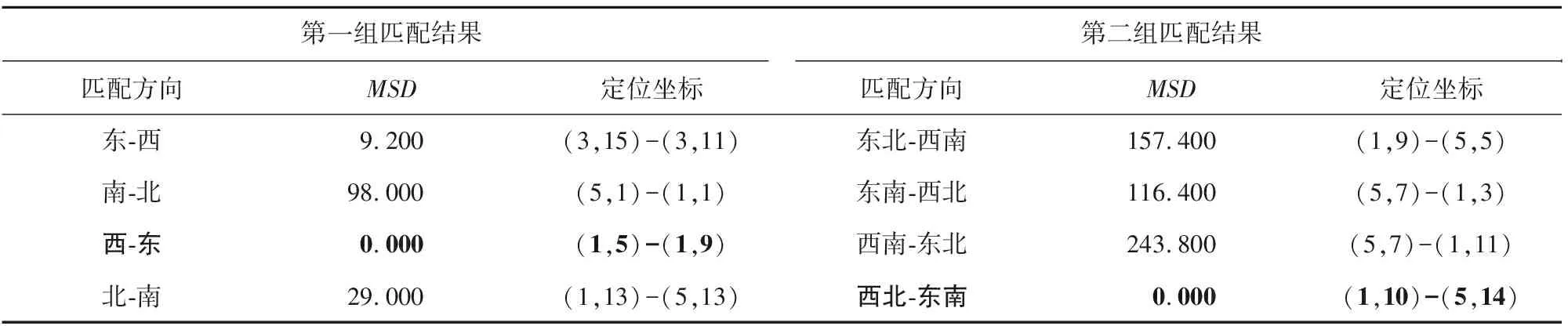
第一组匹配结果第二组匹配结果匹配方向MSD定位坐标匹配方向MSD定位坐标东-西9.200(3,15)-(3,11)东北-西南157.400(1,9)-(5,5)南-北98.000(5,1)-(1,1)东南-西北116.400(5,7)-(1,3)西-东0.000(1,5)-(1,9)西南-东北243.800(5,7)-(1,11)北-南29.000(1,13)-(5,13)西北-东南0.000(1,10)-(5,14)

2.2 实际海图航路规划效果比对

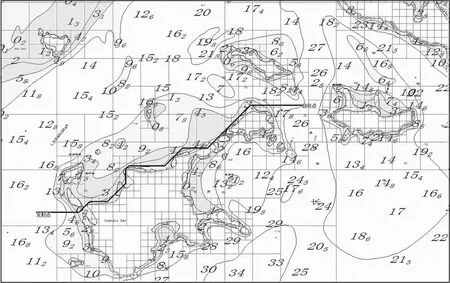
图12 网格化海图上的隐蔽性航路(小范围)

构建应用四叉树算法网格化的海图，同时满足海图的比例尺在可用于匹配定位的范围内。利用对实际海图的仿真实验进一步验证所构建海图的可靠性。对某型低空舰载导弹的若干参数进行如下设定：导弹的回转半径极小值和发射稳定初始航段值均设置为2个单位网格(即划分的顶层网格)，末端攻击前航段值为3个单位网格，极限回转角度为90°。顾及岛屿沿岸轮廓的可匹配定位区域，并应用蚁群算法附加沿岸约束生成的隐蔽性规划航路效果见图12所示，该航路的绝大部分经过岛屿边界区域上空，为地形/水深匹配定位提供可匹配区域时，能够保持一定程度上的匹配连续性。同时，与完全在海域上空巡航的航路相比，由于受海陆交接区域地物效应的影响，依据本文构建海图生成的航路更具有战术隐蔽性。此外，与越岛飞行的航路相比，需要利用的地理信息数据更为简化。最后，从四叉树网格化的划分角度考虑，通过对岛屿边界进行较为细致化的划分，使得匹配区域的特征更加明显，增强了导弹低空飞行对关键区域匹配的时效性。

图12所示的隐蔽航路效果是在小范围、少数岛屿的情况下进行的，生成的合理的规划航路很好地说明了本研究所提构建海图的方法具有一定的适用性。

为了进一步对比验证海图的实际应用效果以及在复杂海图区域的适用性，需要选取范围较大的海域，同时确保该海域的岛屿和沿岸地带较为丰富，方便提取更多的轮廓线来进行仿真验证。此外，在海图构建方面，需利用规则网格构建的海图与四叉树算法构建的海图对比，说明两者的差异及四叉树算法的优异性。如图13所示的岛礁、沿岸区域为规则网格化的海图，图14为在同一岛礁、沿岸区域中应用四叉树算法网格化的海图，可见两幅图中岛屿个数较多、分布较为集中。在确保满足极限航程、转向角度合理等自身约束条件下，应用蚁群算法附加沿岸约束条件得到图13、图14所示的规划航路，图14所示航路相比较于规则网格的规划航路，在一定程度上依托了岛屿边界，使得低空导弹经过海陆交接区域时，产生地物效应从而干扰侦察雷达信号，增强了低空巡航过程中的隐蔽突防能力。表4列出了图13和图14所示航路的具体参数值，通过进一步对比表中数据可知，依据规则格网进行航路规划时，由于航路大部分在海区上方，水深过深而无法进行激光测距，所以无法提供较多的可匹配导航区域。相反，隐蔽规划航路虽然在总航程方面处于劣势，但其规划航路却经过了较多的浅水点的区域，可以给匹配定位提供较为连续的可匹配导航区域。并且由于四叉树算法网格化海图的存储信息量有所简化，节约了整个航路的规划用时。在隐蔽能力上，规则格网化海图的航路绝大部分经过海域，无法充分利用地物效应对敌方雷达侦察造成干扰，从而增加了被雷达持续跟踪、暴露战术意图的概率。而四叉树算法网格化海图的航路，相比而言经过海域的部分要少的多，更多的是经过了海陆交接的区域，增强了地物效应的影响，使得雷达不能持续捕获跟踪，增强了导弹的隐蔽能力。

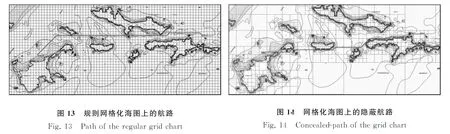
表4 规划航路参数对比表

3 结论

通过分析计算及海图仿真实验，得出以下结论：

1) 以岛屿、海岸轮廓线为基础，应用四叉树算法构建的网格化海图，能够充分利用地物、海面的多路径干涉效应来躲避敌方雷达，从而为规划具有隐蔽性的航路提供了保障。

2) 在规划隐蔽性航路基础上，四叉树算法网格化的海图提供了较为连续的可匹配定位区域用于匹配导航定位，扩大了低空舰载导弹的匹配导航定位的区域范围，有效提高了导航能力。

由于本文从矢量海图网格化方法应用的角度出发，忽略了潮汐规律对岛屿、海岸轮廓线的影响，也未能深入研究匹配定位与航路规划之间的反馈作用，还需要在下一步研究过程中完善海图精度、潮汐变化对海图构建的影响及海图容错性的分析。