随机利率下由Lévy过程驱动的期权定价

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

随着现代资本市场的不断发展，国内金融衍生产品市场迎来蓬勃发展的大时代。期权作为全球最为活跃的金融衍生产品之一，是金融产品创新的前沿，与现货、期货一同组成稳定的金融体系。期权受市场中利率波动的影响，各种利率衍生产品的交易成为期权定价研究领域的热点问题之一。

对金融及其衍生产品给出一个合理的、使市场无套利的定价是当前研究的首要问题。然而在现实市场中利率不是一个常数，它是随机变化的。许多学者在此基础上进行了诸多研究：李淑锦[1]利用计价单位转换的方法研究了随机利率服从HJM模型条件下的期权定价问题，推导出了期权定价公式。刘坚等[2]在假设利率服从Hull-White模型、资产价格服从O-U过程条件下，利用保险精算方法给出了期权定价的公式。郭精军等[3]利用对冲原理构造无风险资产，求得欧式期权在随机利率模型下满足的偏微分方程，经过变量替换获得了欧式期权定价公式。1973年，Black和Scholes[4]假定股票价格过程服从几何布朗运动，提出了经典的B-S期权定价公式。但这一条件要求过于苛刻，实际情况中股票的价格变化并不是完全服从布朗运动的。1988年，Lo等[5]在B-S公式基础上提出股票价格存在“跳跃”的情况。此后越来越多的学者对标的资产价格存在跳跃的情况进行研究。黄伯强等[6-7]借助等价测度变换方法研究由Lévy过程驱动的期权定价问题，推导出了欧式期权定价公式。吴恒煜等[8]在此基础上就无穷维纯跳跃Lévy过程的期权定价问题进行了研究。鲍家勇等[9]利用傅里叶变换方法研究了资产价格服从随机利率下由Lévy过程驱动的欧式期权定价。在假设利率是一个常数的条件下，文献[10]研究了knight不确定环境下的lévy型金融市场中的期权定价问题，并得到了欧式期权动态模型定价区间。然而，在实际市场中，利率是随时变化的，在随机利率条件下给出确定性的期权定价公式，更能精确地预测金融市场中资产价格的变化情况。

本研究在利率随机且服从Ho-Lee模型的条件下，借助Lévy-Laplace指数数学工具得到无套利条件下欧式看涨、看跌期权定价公式，并与标准的B-S期权定价公式进行比较，同时对股票价格服从Lévy纯跳跃过程的期权定价问题进行进一步研究，利用泊松过程的性质得到Lévy-Laplace指数，建立无套利金融市场下带跳的欧式期权定价模型，得到无套利约束条件下的欧式期权定价公式，拓展已有文献的结论。

1 基本模型介绍

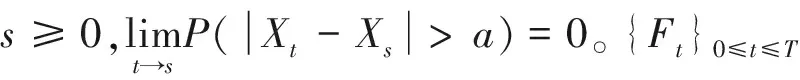
1.1 股票价格模型

假设Lévy过程{Xt}0≤t≤T的Laplace变换E[eλXt]有界，设0≤t≤T时刻股票的价格为S(t)，则标的股票价格过程为：

(1)

其中，μ、σ为常数，分别表示股票价格的期望收益率和波动率，且假设σ大于0，Bt是标准的一维布朗运动,S0是初始时刻股票价格。

引理1[11](Lévy-Laplace指数)Xt为Lévy过程，对任意t∈R+,λ∈(-∞,λu],λu≥0,存在一个函数Φ:(-∞,λu]→R使得E[eλXt]=etΦ(λ),称Φ(λ)是Lévy过程Xt的Lévy-Laplace指数。

1.2 随机利率模型

假设金融市场上的利率是随机波动的，而金融产品的价格又受利率随机波动的影响，基于此，对市场利率服从Ho-Lee模型的欧式期权价格进行讨论。

Ho-Lee模型的利率随机波动满足

dr(t)=θ(t)dt+σrdB(t)。

其中，σr表示市场利率的波动率，θ(t)是关于时间t的函数。特别地，当θ(t)=0,r(0)=r时，上述模型将化为：

(2)

方程(2)所体现的利率瞬时运动只有扩散项σrdBt，而没有漂移项，这说明了利率只是围绕某一固定的常数值随机波动，本身并没有稳定移动的趋势，初始值为r。这种利率模型在金融市场上有一定的市场解释(文献[11]曾利用该模型研究远期的定价和风险研究)。在此模型基础上，研究期权定价问题，该利率模型的解析形式为：

(3)

2 随机利率环境下的期权定价

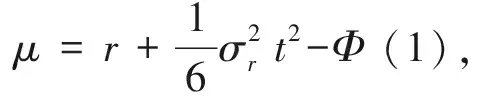
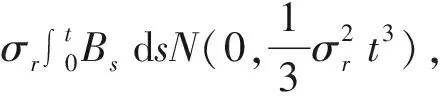
且由引理1可得

定理2在定理1条件下，利率随机且运动方程满足公式(2)时，欧式看涨、看跌期权的定价公式分别为：

(4)

(5)

其中，Ct、Pt分别表示到期日t时刻看涨期权以及看跌期权的价格，K表示敲定价格，σ、σr分别表示金融市场上股票价格和市场利率的波动率。

证明：在定理1条件下，欧式看涨期权

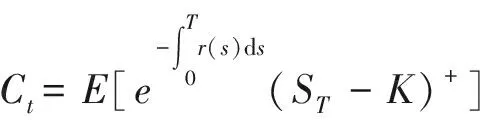
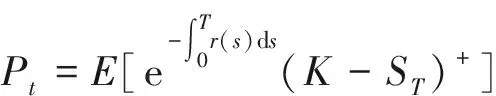
由上述定理可知，若不考虑随机利率的影响，由标准布朗运动驱动下的标的股票价格过程的欧式看涨、看跌期权定价公式分别为

(6)

(7)

则利率随机服从Ho-Lee模型下标的股票价格过程由Lévy驱动的欧式看涨、看跌期权的定价公式可分别记为：

(8)

(9)

由上可知，Ho-Lee模型下由Lévy过程驱动的股票价格的期权定价公式在形式上与传统的B-S期权定价公式一致，可看作是对B-S公式的推广。

3 Ho-Lee模型下Lévy纯跳驱动下的期权定价

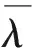
1)N(0)=0；

2)N(t)是独立增量过程；

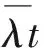
且V={Vi}i∈N+，Vi表示第i次跳跃的幅度，并且它是独立同分布的跃度随机变量，且满足下列条件：

1)V0=1,Vi∈(-1,+∞);

2)对任意的v∈(-∞,1)，有E[(1+V)v]<∞。

Ft是由{Bt}0≤t≤T,{Nt}0≤t≤T和{Vi}i∈N+共同生成的σ-域流，三者彼此独立。此时股票价格过程为：

(10)

由Possion过程的性质可得到：

定理3在无套利约束条件下，股票价格过程(10)的欧式看涨期权的定价公式为：

(11)

其中，

假设跃度Vi=h≠0(i=1,2,…)。

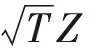
(12)

因此

从而:

(13)

则由ST>K,计算公式(13)括号中的表达式。即

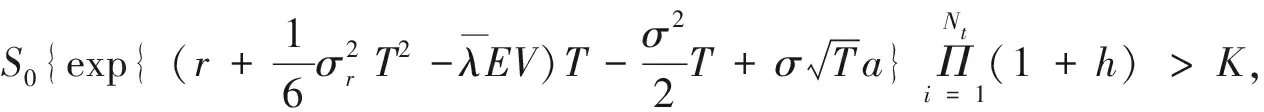
可得期权价格

(14)

把上述积分分成两部分：

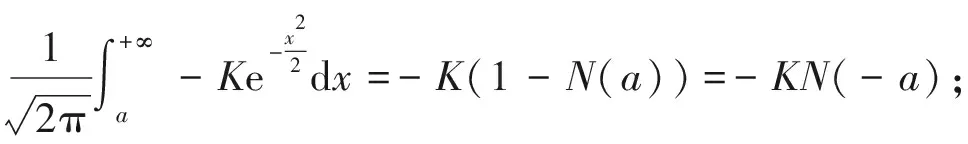
(15)

第一项

(16)

记

将式(15)、(16)代入式(14)可得看涨期权的定价公式

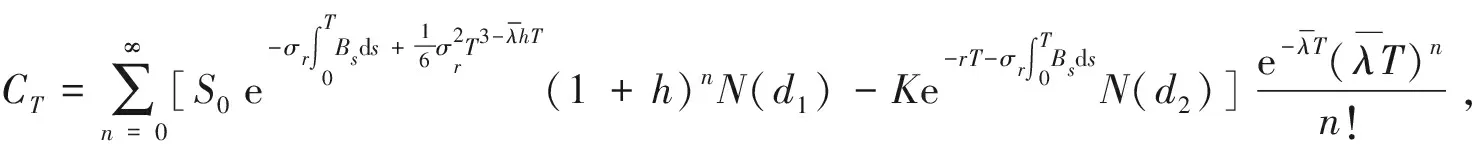
4 小结

在金融市场中，期权的价格不仅受标的价格变动的影响，而且与利率的波动密切相关。利率是决定所有金融衍生产品价格的一个重要因素，考虑了利率的随机性对股票价格的影响，将利率服从Ho-Lee模型和标的资产服从Lévy驱动的过程结合在一起，建立了新的随机微分方程，使得股票定价更加贴合实际。利用Lévy-Laplace指数研究了欧式期权定价问题，研究了在股票价格存在连续跳跃的情况下，借助Poisson过程和Lévy-Laplace指数数学工具得到了无套利金融市场下欧式看涨期权定价公式。本研究进一步丰富和拓展了文献[4]中的期权定价理论，结论可进一步拓展到其他类型期权的定价研究中。