基于信息熵的溶解氧传感器数据融合处理方法

(1. 山东科技大学 测绘科学与工程学院，山东 青岛 266590；2. 齐鲁工业大学(山东省科学院) 海洋仪器仪表研究所，山东 青岛 266061；3. 自然资源部 第一海洋研究所，山东 青岛 266061)

海水溶解氧是维持海洋生物生存的重要物质，是评价水体受污染情况的重要指标。快速准确、长期连续地监测水体溶解氧浓度对于海洋环境保护、水质生态危机预报预警、海岸带综合修复状况评价以及科学指导水产养殖都具有重要意义[1]。现有的基于荧光猝灭原理的光学溶解氧传感器，尤其是国产传感器存在连续工作稳定性可靠性差、易污染、易生物附着、测量数据易漂移等问题[1]。究其原因，在于不论何种测控应用场景，依赖各类传感器测量获得的结果均存在一定程度的数据不确定性。这种不确定性来源于操作误差、仪器设备精确度、传输干扰或数据处理误差等因素，因此必须对测控系统的传感器输出采取必要处理，确保数据有效性。

现阶段，各类测控场景应用最多的方法是信息融合，也称数据融合。其主要思想是以多种渠道或多组测量获取的数据全体为依据，采用一定的算法逻辑，开展数据筛选、提前和整合，获得的融合后数据比原始数据更加真实、可信。针对这类问题，文献[2-5]进行了多传感器测量数据融合的相关探索和研究。然而在各类工控领域，独立传感器测量或多传感器独立分布、组网测量的方式仍在被广泛使用，而且对这类独立使用的传感器测量数据的不确定性剔除和融合处理方面的研究仍较少[6-8]。最常用的算术平均法，计算量少、速度快，但是对所有样本采用同样权值进行运算，融合结果易受到各种不确定性因素的影响。文献[6]设计了一种基于统计加权的融合算法，依据测量结果偏离融合结果的程度赋予不同权值，能在一定程度上削弱主观因素对融合值的影响，但存在迭代计算量大、收敛速度慢的缺陷。文献[7]介绍了一种基于最大熵的测量结果估计方法，单选用样本概率作为数据融合权系数，难以削弱融合结果对不确定性因素的敏感程度。文献[8]提出一种改进的分批估计融合算法，但算法的应用必须以传感器测量值样本符合正态分布特性为前提，存在明显局限性。因此，研究单传感器测量系统数据融合方法来提高测量数据准确性和可靠性，仍具有十分重要的意义。

本研究在自主研制的HJY1-1型光学溶解氧传感器的基础上[9]，从Shannon提出的信息熵概念[10-13]出发，针对该型溶解氧传感器标定数据融合问题，提出一种基于信息熵的单传感器数据融合处理方法，力图解决上述算法在单传感器测控系统适用性与测量数据分布局限性方面的不足。在此基础上，结合光学溶解氧传感器标定实验测量数据，对方法有效性作出评估。

1 基于信息熵的溶解氧传感器数据融合处理方法

本方法主要思想是：首先利用最大熵方法(maximum entropy method，MEM)估计获得离散传感器数据的概率分布[13]，然后根据求得的标定实验测量的不确定度确定置信区间，依托该置信区间，进行粗差辨别和剔除[14-17]。最后，针对有效标定数据，计算样本自信息量与信息比率，根据定义的融合权系数完成数据融合处理，得到最终的融合结果。该方法步骤如流程图1所示。

1.1 基于最大熵方法的离散样本概率分布估计

最大熵方法是指在仅能获知局部信息的条件下对开展系统状态估计时, 所选择的合理状态应为信息熵值最大且符合约束条件的那组, 是现有条件下能做出的唯一公正的选择, 所有选择的其他状态都代表改变了原有假设或添加了其他约束，无法做到不偏不倚[14]。因此，对于单传感器测量控制系统而言，如果条件只允许获得传感器测量值样本数据，而不能够根据已有条件获得该独立传感器输出测量值的概率分布的，就能够利用该最大熵方法，获得该独立传感器测量输出值最公平的概率分布情况。

对于光学溶解氧传感器标定实验，假设每组浓度梯度处，水体溶解氧含量稳定后，待标定传感器对溶解氧浓度参数进行k次独立重复测量，获得的样本数据表示为m1,m2,…,mk。由于实际标定实验中，对每组溶解氧浓度梯度处的测量为有限次，因此，获得的测量列是一列离散值。由Shannon信息熵定义，计算测量列最大离散熵来估计样本数据的概率分布形式。

离散随机变量M的最大离散熵为：

(1)

其中，P(mi)为每组溶解氧浓度梯度处的测量数据样本的概率，其满足约束条件为：

(2)

其中，〈fn(mi)〉为若干函数fn(mi)的期望值，N为期望函数的个数。

运用拉格朗日乘数法可计算该概率分布及对应的最大熵，计算公式如式(3)、(4)所示。

(3)

(4)

其中，λ0和λn为引入的相应拉格朗日乘数，Hmax为所求的最大离散熵。

对于光学溶解氧传感器标定实验这类独立传感器重复测量的情形，在获取溶解氧传感器测量示值作为样本点的基础上，依据离散标定数据列的方差与数学期望，构造该标定实验数据的期望函数，进行后续运算处理。

1.2 基于最大离散熵的粗差剔除

当单传感器独立使用时，整个测控系统采集的有效监测数据不足或采样频率不高、次数较少的情况下，获得的有效样本空间的大小将不足以满足统计规律，难以获得测量值的概率分布。传统的、建立在数理统计基础上的粗差判别准则将很难适用[16]。

在获得最大离散熵概率分布的基础上，估计出测量列的概率密度函数为P(mi)，故离散测量列的不确定度为：

(5)

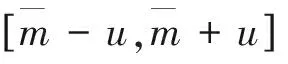
进一步地，以此置信区间为依据，判定不在该区间范围内的数据为粗差，剔除这些粗差后获得新的纯净数据序列，开展后续融合处理。

1.3 基于信息熵的数据融合处理

由Shannon信息熵定义可知，信息熵是信息量的度量，是衡量不确定性程度的指标[11,13]。根据测量样本数据的不确定性大小来分配不同的权系数，进行数据融合，能够有效削弱融合结果对不确定性因素的敏感程度[16-17]。因此，基于信息熵的数据融合理论，可以用来进行单传感器测量数据的修正处理。

对于光学溶解氧传感器标定实验这类单传感器独立重复观测，需要借助自信息量I(mi)来表征不同浓度梯度下的每组传感器测量样本mi所携带的信息。同时，可以借助信息熵来表征样本总体的测量不确定程度。在此基础上，通过定义每个样本自身的信息比率来表征其在样本总体中的不确定性。显然，在工程实际应用中，对于每个单传感器输出测量值，距离真值越远，则表示该测量值产生的概率越低，对应的自信息量越丰富；相反地，测差值距离真值越近，该测量值产生的概率越高，对应的自信息量越微弱。由此可知，传感器测量数据自信息量与融合时相应的权系数呈反比关系。

根据以上分析，设计的适用于光学溶解氧传感器标定数据处理的融合算法步骤如下：

1) 根据获得的离散测量样本，估计数据的最大熵分布；

2) 求出标定实验中，每种情况下传感器测量输出值的自信息量I(mi)；

3) 计算信息比率ηi，即单个测量数据在总体测量数据中的不确定性程度，即：

(6)

其中，I(mi)=-logP(mi)。

4) 规定数据融合权系数，进行归一化处理，有：

(7)

5) 针对剔除粗差后的有效数据，进行数据融合，即：

(8)

图2 光学溶解氧传感器新型标定装置与HJY1-1型光学溶解氧传感器

2 实验验证

2.1 实验情况说明

采用如图2所示的光学溶解氧传感器新型标定装置，对HJY1-1型光学溶解氧传感器进行标定实验。利用获取的标定实验数据，对本方法的有效性进行评估。

2.2 实验数据分析

针对任意设定温度下的每一处溶解氧浓度点，均可以获得如表1所示的一组测量样本数据。表1中数据表示用同一款光学溶解氧传感器在同一温度和同一溶解氧浓度条件下，连续进行多次采样，获得的8个溶解氧浓度测量样本数据。此处设定的环境水温为5 ℃，水体溶解氧含量保持恒定，采用国标碘量法(GB 7489—87)测得的结果为8.37 mg·L-1。

表1 光学溶解氧传感器在设定温度及浓度情况下8个样本数据

选取测量样本数据的绝对误差和均方误差作为衡量数据融合效果的精度指标。表1中，8组测量数据的期望和方差分别为：

离散测量数据样本概率分布满足的约束条件有：

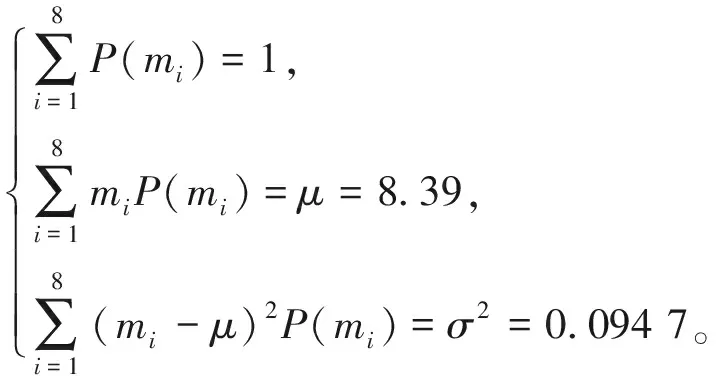
运用MATLAB软件，根据最大熵方法，按照拉格朗日乘数法计算得到拉格朗日系数，分别为：-4.69、0.69、5.97，进而可得该组离散测量数据概率分布为：

P(mi)=exp[4.69-0.69mi-5.97(mi-9.39)2]。

最大离散熵为：

Hmax=1.819 9。

测量数据自信息量为：

I(mi)=-[4.69-0.69mi-5.97(mi-8.39)2]。

表1中8组测量数据对应的概率和自信息量如表2所列。

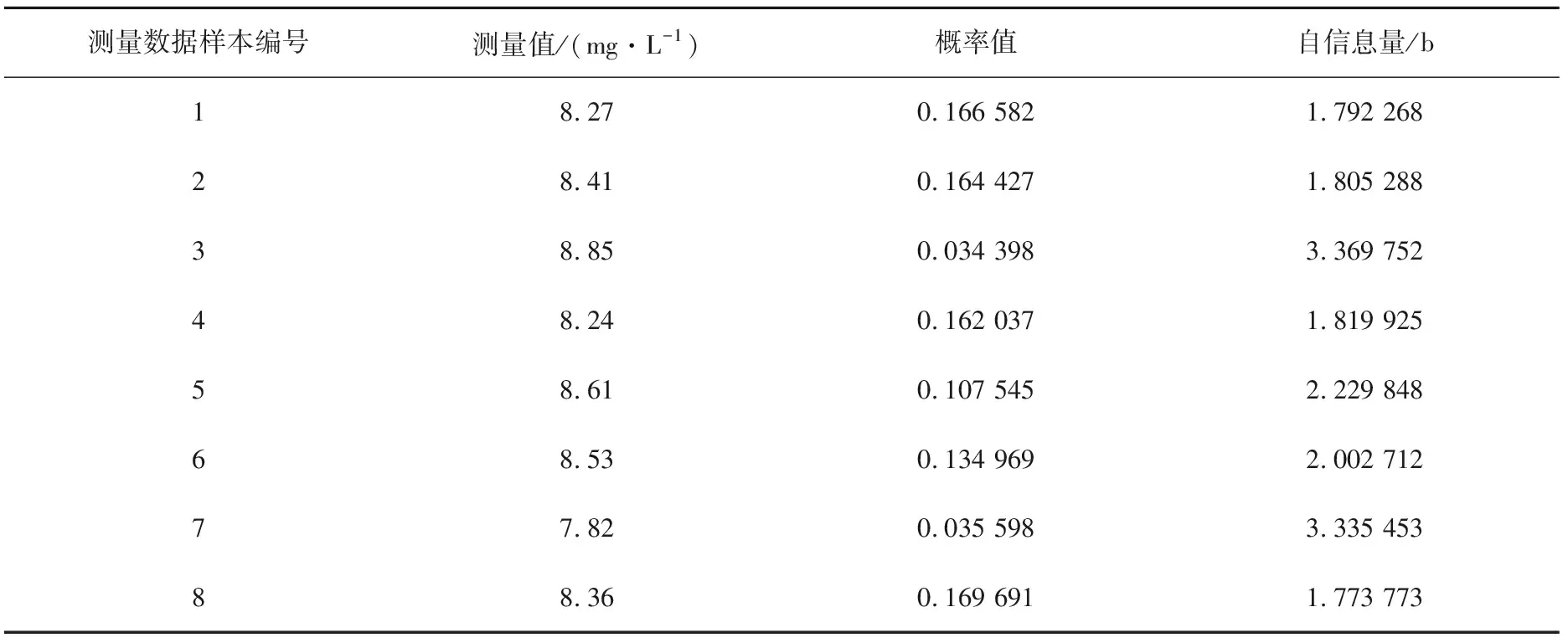
表2 本情况下8组溶解氧传感器测量输出值的概率以及对应自信息量

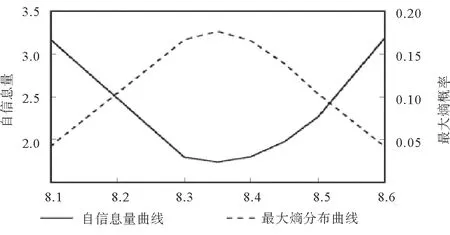
图3 测量数据的自信息量和概率分布曲线

结合表2中数据，可得该组溶解氧浓度条件下全部测量数据的自信息量以及最大熵分布曲线图，详见图3。不难得出下面结论，若传感器测量输出结果距离溶解氧含量真值(即国标碘量法测定溶解氧浓度)越远，其自信息量越大、概率越小；距离溶解氧含量真值越近，自信息量越小、概率越大。

由测量数据的最大离散熵概率分布，可得测量的不确定度为：

故可以推定，该组测量数据的有效置信区间为：

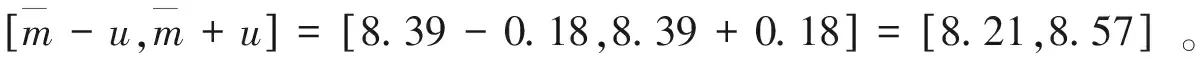
依据该有效置信区间，进行粗大误差判别。经过判断，该组测量数据8个样本中，第3、5、7个样本包括粗大误差，必须被剔除出有效测量序列。在获得自信息量的基础上，根据算法公式(7)融合权系数的定义，计算剩余5个离散测量样本融合权系数，进行测量数据融合运算。需要特别说明的是，当离散的传感器测量数据列已经完成粗差剔除工作后，不同的数据组合，不影响后续的融合权确定和最终融合结果的运算。综上所述，该组测量样本的数据融合结果为8.36 mg·L-1，具体运算数据如表3所列。

表3 本组实验条件下5个纯净测量结果融合权系数情况

针对该组测量数据，选取除本算法外的其他多种算法进行数据融合计算。统一将国标碘量法的测点结果8.37 mg·L-1作为真值，选取绝对误差和均方误差作为判定融合效果的精度指标，与文献[6-8]中各种方法及传统算术平均法融合结果对比如表4所列。

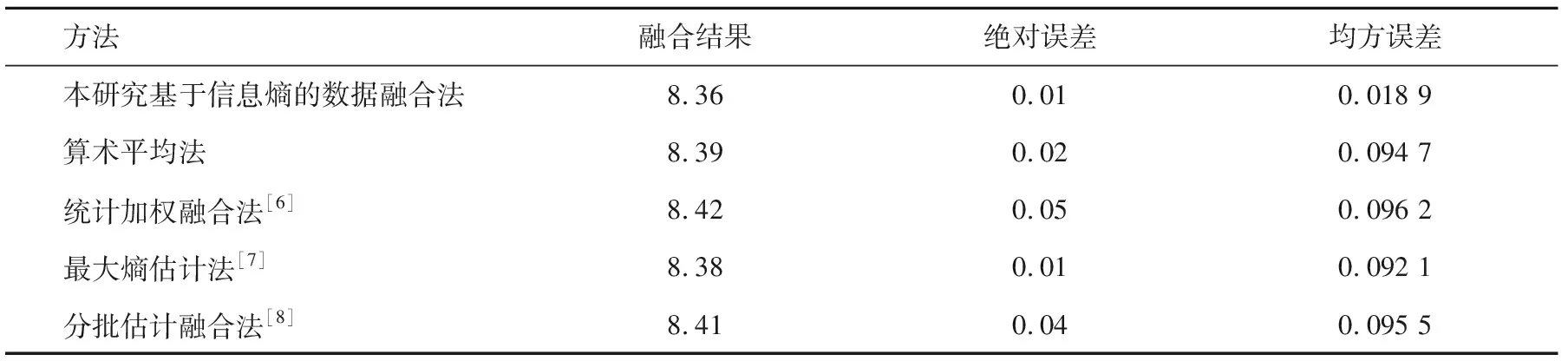
表4 5种算法数据融合结果对比

从表4可看出，以水体溶解氧浓度测量的国标碘量法测量结果(8.37 mg·L-1)为标准，基于信息熵的数据融合算法拥有最小的绝对误差，并且均方误差也显著降低。因此，基于信息熵理论针对光学溶解氧传感器标定数据融合提出的算法，能够明显提高传感器整体的工作可靠性和测量数据稳定性，有效提升标定实验的效果。

3 结论

针对光学溶解氧传感器标定过程的各浓度梯度处标定测量样本有效融合的问题，提出一种基于标定实验离散测量数据信息熵的数据融合算法，解决了国产光学溶解氧传感器标定过程中的单传感器测量数据处理的难题。该算法从独立传感器测量数据最大离散熵入手，获得样本数据的概率分布，进而计算离散测量数据的不确定度，并据此进行粗差剔除。在此基础上，对置信区间内的有效测量数据，通过自信息量与权系数的计算，进行合理数据融合。结合HJY1-1光学溶解氧传感器标定应用实例，验证了该算法能够有效避免单传感器测量使用情况下的各种不确定、非线性因素对测量结果的影响。对比其他4种算法，本文算法在多种精度指标上均表现出明显优势，能够有效提升测量数据的准确性和可靠性。与此同时，针对光学溶解氧传感器标定实验进行的相关研究，对于其他各类海洋传感器的实验室标定校准工作，均能提供一定的参考和借鉴。不足之处在于，本次实验覆盖的温度区间有限，获得的有效算例不够丰富，在后续研究工作中，将进一步完善充实。