基于EKF的GNSS/SINS组合导航系统应用

,王海霞,陈云

(1.山东科技大学 山东省机器人与智能技术重点实验室，山东 青岛 266590；2.山东科技大学 海洋工程研究院，山东 青岛 266590；3.山东科技大学 电气信息系，山东 济南 250031)

为获得更高精度的定位结果，将多种导航定位技术组合，已成为导航定位的热门发展方向。全球卫星导航系统(global navigation satellite system, GNSS)是全球所有的卫星导航系统的总称，包括GPS(美国)、GLONASS(俄罗斯)、GALILEO(欧洲)和 BDS(中国)等卫星导航系统。随着各导航系统的不断发展建设，多频多系统GNSS应用已成为卫星导航定位系统的主要发展趋势之一。与单一系统相比，GNSS系统可以为卫星导航系统提供更丰富的可用信号，更好的星座条件，获得更高精度的载体三维位置信息[1]。然而，当卫星信号被遮挡或受到干扰时，如在室内、高楼密集的城市、茂密的树林、海上等环境，GNSS系统无法得到稳定、持续的定位信息。惯性导航系统(inertial navigation system, INS)是一种自主式导航系统，依据惯性工作原理，应用陀螺仪、加速度计等惯性元件测得载体的角速度、加速度，然后通过积分得到其位置、速度和姿态等定位信息。INS具有自主性、隐蔽性及连续提供位置、速度、姿态信息等优点，但其导航误差会随时间增加而积累，严重影响定位的精度，不适合长时间连续工作[2]。INS主要包括平台惯性导航系统(platform inertial navigation system, PINS)和捷联惯性导航系统(strapdown inertial navigation system, SINS)，二者本质相同，但PINS采用物理平台模拟导航坐标系，而SINS采用的是数学平台。SINS由于具有结构简单、体积小、重量轻、成本低和可靠性高等优点，逐渐成为目前最常用的惯性导航系统[3]。

通过以上分析可发现，若将两者结合起来，GNSS与SINS就能达到优势互补的效果[4-6]。当卫星信号接收良好时，利用GNSS的定位结果对SINS定位结果进行校正，消除SINS的累积误差；当卫星信号受到遮挡时，SINS发挥短时间内定位精度高的优点单独进行定位，可以持续得到高精度、高可靠性的导航信息。文献[11]对基于扩展卡尔曼滤波(extended Kalman filter, EKF)的GNSS/SINS深组合导航系统进行仿真，其位置误差较大，地向误差达到10 m左右。文献[12]对GPS/SINS紧密组合导航系统进行了仿真研究，表明紧密组合导航比松散组合导航收敛性更好、精度更高，仿真实验的位置误差在0.5 m左右。文献[13]通过仿真实验证明基于EKF的GPS/SINS松组合导航算法能对载体的速度和姿态实现有效跟踪，但没有给出是否能对载体的位置进行有效跟踪，且载体的导航误差8 min后才收敛，位置误差最低值在5 m·s-1左右。本研究针对GNSS、SINS单独应用时存在不足的问题，将两者组合，并通过车载实验采集导航数据，利用EKF算法对GNSS/SINS组合导航系统进行解算，得到的位置误差、速度误差及姿态误差都快速收敛，且位置误差精度保持在厘米级，速度误差在0.1 m·s-1以内。

1 捷联惯性导航

1.1 捷联惯性导航系统基本原理

SINS属于递推导航系统，以初始对准得到的初始姿态、载体的初始位置、速度为基础，利用陀螺仪、加速度计得到角速率及比力值，再通过捷联惯性导航算法推算出下一时刻载体的姿态、位置、速度信息。以此类推，可以计算出载体每一时刻的导航信息。SINS的数据更新频率高，且在短时间内拥有较高的导航精度。

1.2 捷联惯性导航系统基本方程

采用当地地理坐标系作为导航坐标系(n系), 当地地理坐标系也称为东北天(east-north-up, ENU)坐标系[7]。SINS导航方程[8-9]主要包括姿态微分方程、速度微分方程和位置微分方程：

1) SINS的姿态微分方程为：

(1)

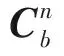
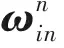
(2)

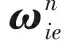
2) SINS的速度微分方程为：

(3)

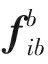
3) SINS的位置微分方程为：

(4)

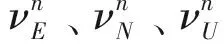
2 GNSS/SINS组合导航

2.1 GNSS/SINS组合导航原理

研究的组合导航[9]形式为松组合，松组合中SINS的加速度计、陀螺仪分别输出载体当前的比力、角速度信息，通过捷联惯性导航解算系统可求得位置PSINS、速度VSINS、姿态矩阵；而通过GNSS得到位置PGNSS、速度VGNSS。SINS与GNSS的位置、速度的差值为扩展卡尔曼滤波器的输入，通过组合导航算法得到惯导系统状态误差估计值[10-11]，利用该误差估计值对捷联惯导系统输出值进行校正，最后得到高精度、稳定连续的载体位置、速度及姿态信息。其原理图如图1所示。

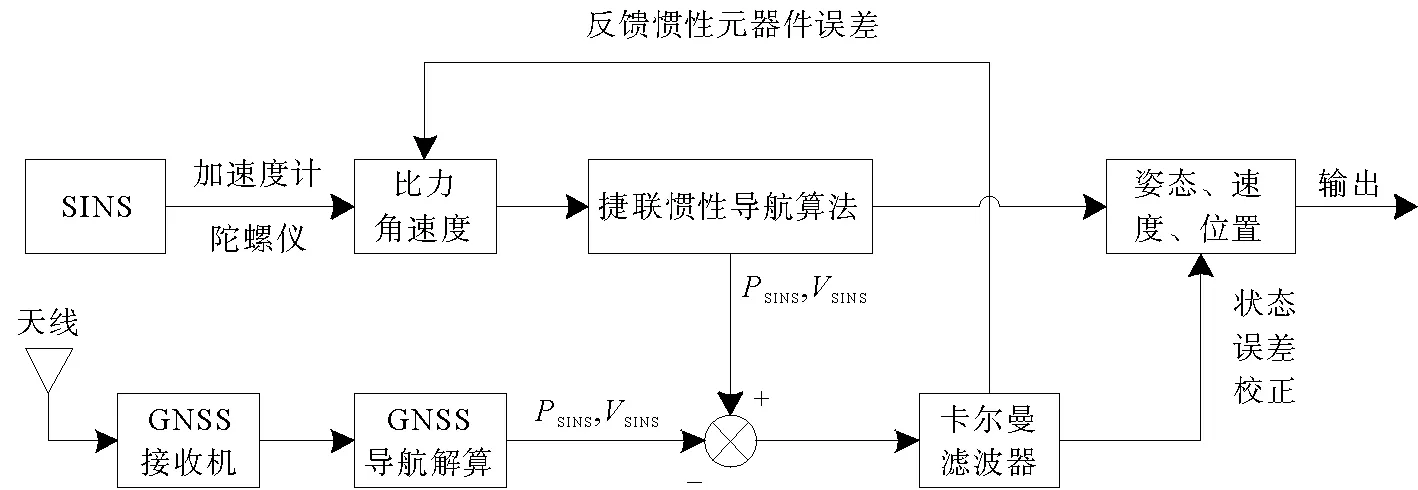
图1 GNSS/SINS组合导航原理图Fig.1 Schematic of the integrated navigation of GNSS/SINS

2.2 GNSS/SINS组合导航模型

GNSS/SINS组合导航模型将惯导误差方程、GNSS定位测速的误差方程分别作为系统状态方程和量测方程的基础，该系统的状态变量是由姿态误差、速度误差、位置误差、陀螺仪测量误差及加速度计测量误差组成的15维向量组成[12]，即

X=[φE,φN,φU,δνE,δνN,δνU,δL,δλ,δh,εx,εy,εz,▽x,▽y,▽z]T。

(5)

系统的状态方程和量测方程[13]分别为：

(6)

式中：F(t)为系统状态矩阵；G(t)为系统噪声矩阵；Wd(t)为系统噪声向量；Z(t)为量测向量；H(t)为量测矩阵；V(t)为量测噪声向量。Wd(t)与V(t)均服从零均值白噪声，相互独立且互不相关。

式(6)中的系统状态方程和量测方程是线性连续的，为了能够在计算机中实现对数据的编程处理，需将其进行离散化处理[14]，即

(7)

式中：Xk-1、Xk分别为k-1、k时刻系统的状态向量；Φk,k-1为k-1时刻至k时刻的系统状态转移矩阵；Γk-1为k-1时刻的系统噪声驱动矩阵；Wk-1为k-1时刻的系统噪声向量；Zk为k时刻的量测向量；Hk为k时刻的量测矩阵；Vk为k时刻的量测噪声向量。

3 EKF算法

卡尔曼滤波(Kalman filter, KF)是状态估计算法的基础，同时也是导航系统解算中最常用的滤波方法。KF在处理线性系统时，一般能够得到较好的结果。而GNSS/SINS组合导航系统的本质是非线性系统，使用KF则不能得到理想的滤波结果。1969年，Bucy等[15]提出了扩展卡尔曼滤波算法，并将其成功的在非线性领域中进行应用，其原理是将非线性系统进行泰勒级数展开，只取至一次项，从而得到其线性化的系统模型，解决了非线性系统不能得到理想的滤波结果的问题。

GNSS/SINS组合导航系统采用闭环反馈校正系统，使状态误差能够保持在较小值，提高组合导航定位的精度。扩展卡尔曼滤波过程包括时间更新和量测更新两部分，其基本步骤[9]：

1) 时间更新：

(8)

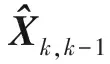
(9)

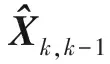
2) 量测更新：

(10)

式中，Rk为k时刻的量测噪声协方差矩阵，Kk为k时刻KF增益矩阵。

Pk=(I-KkHk)Pk,k-1，

(11)

式中，Pk为求得的k时刻系统状态协方差矩阵。

(12)

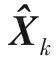
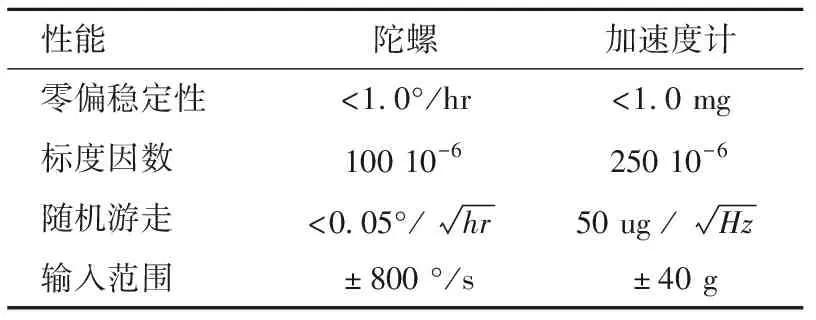
表1 SPAN-LCI惯导性能指标Tab.1 Performance index of the SPAN-LCI

由于SINS数据更新率比GNSS高，当只有SINS数据时，该系统仅进行时间更新过程，当GNSS的数据时间与SINS的一致时，组合导航系统既进行时间更新过程也进行量测更新过程。GNSS与SINS每次组合后的定位结果都会对该时刻SINS的结果进行校正，以消除其累积误差，使GNSS/SINS组合导航系统持续取得高精度的载体导航信息。

4 车载实验及分析

本实验在山东科技大学附近采集车载数据，实验设备为NovAtel的SPAN-LCI战术级IMU惯导、双系统GNSS(GPS、GLONASS)接收机。其中惯导数据的采样频率为200 Hz，GNSS数据的采样频率为5 Hz，惯导比GNSS的数据更新率更高。IMU惯导性能指标如表1所示。在Google Earth上显示的车辆轨迹如图2所示。实验分别对SINS单独导航和GNSS/SINS组合导航进行了定位解算，并将高精度组合导航后处理软件IE 8.6的解算结果作为参照值。其中，在GNSS信号不丢失的情况下，由IE软件处理的位置误差精度水平方向能达到0.01 m，垂直方向能达到0.015 m；其速度误差精度在水平和垂直方向都能达到0.01 m·s-1；其姿态误差中的横滚角、俯仰角误差精度都达到了0.005°，航向角误差精度达到了0.008°[16]。

图 2 Google Earth 中显示的跑车轨迹图Fig. 2 Vehicle trajectory in Google Earth

4.1 SINS单独导航实验

对由SPAN-LCI战术级IMU惯导采集的车载数据单独进行SINS导航解算，得到纯惯导定位在ENU三个方向的位置、速度以及姿态结果，并通过与IE解算的高精度结果比较得到SINS的定位误差，其位置误差、速度误差及姿态误差分别如图3～5所示。

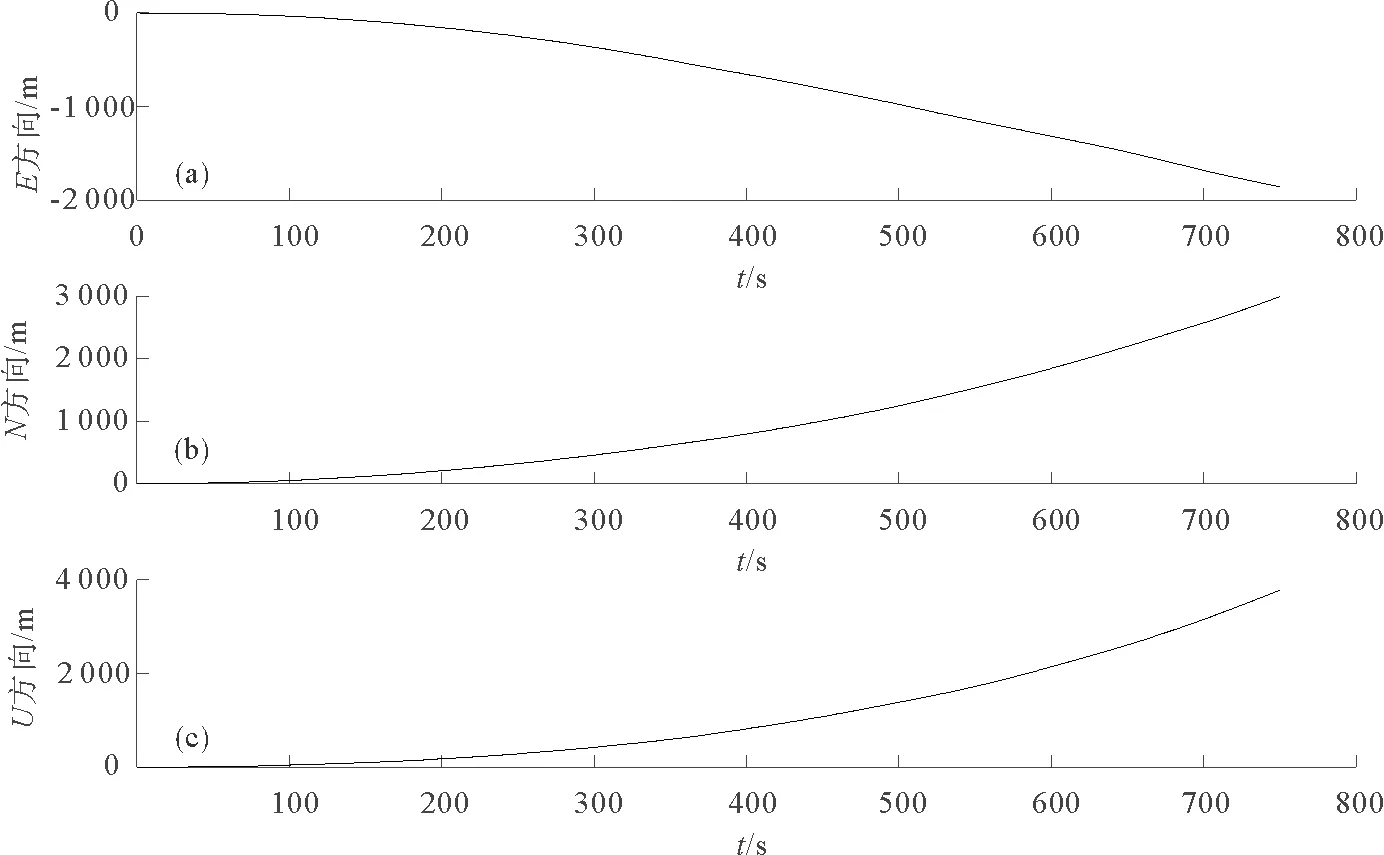
图 3 SINS位置误差Fig. 3 The position error of SINS

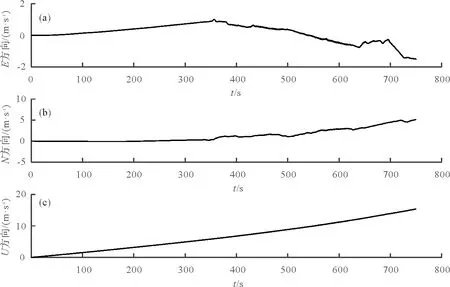
图 4 SINS速度误差Fig. 4 The velocity error of SINS

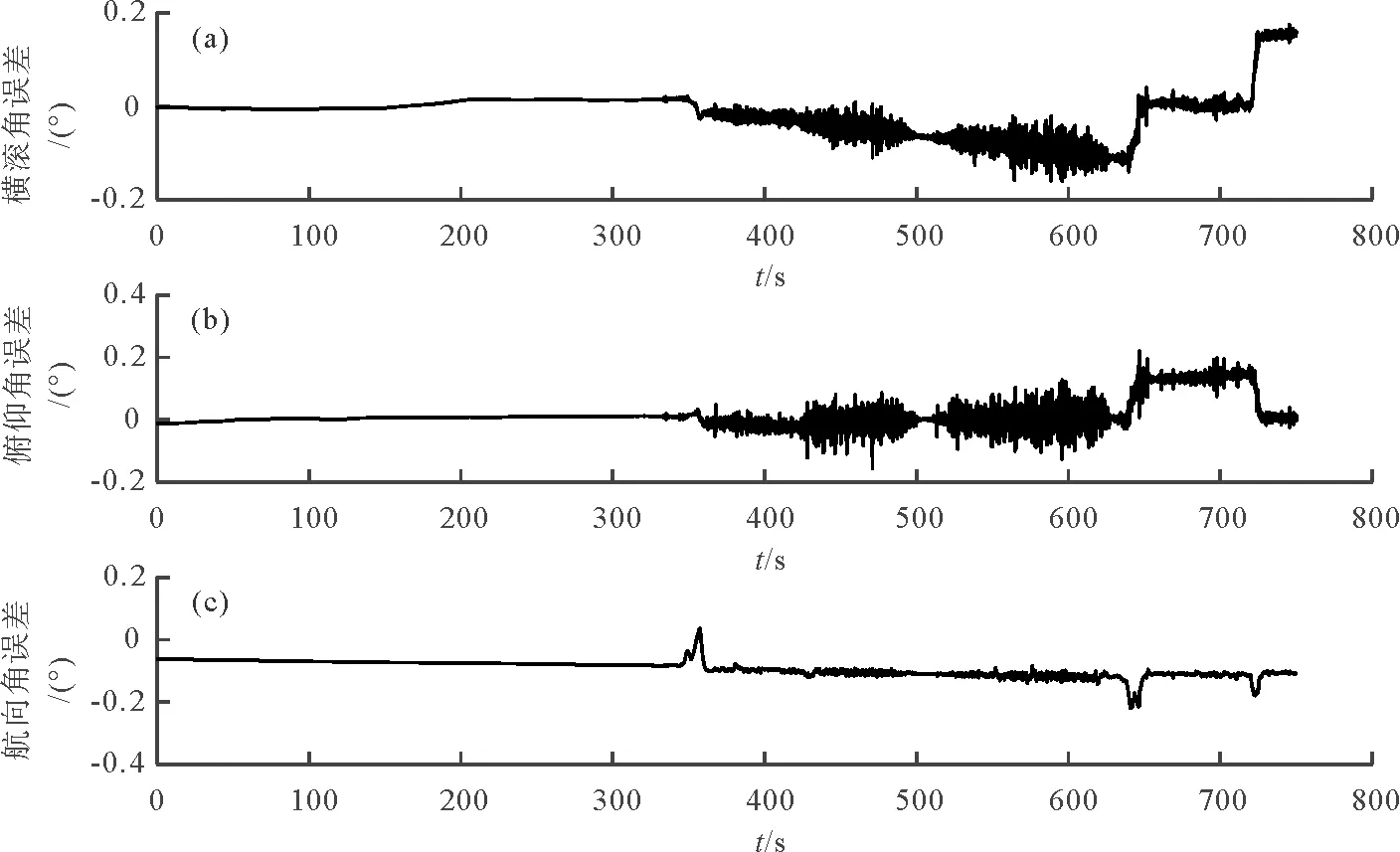
图 5 SINS姿态误差Fig. 5 The attitude error of SINS

由图3可以很明显看出，SINS单独导航时，其ENU三个方向的位置误差只在最开始的短时间内较小，但是随时间的增长，该误差不断累积，最后甚至达到几千米。同样，由图4可得，SINS导航在ENU三个方向的速度误差也随着时间存在不同程度的累积，其中U方向的速度误差累积最大，达到20 m·s-1。而由图5可得，SINS单独导航得到的三种姿态角误差没有随时间的增加不断累积。由此可知，SINS不适合单独导航，需要其他的导航系统的辅助才能消除累积误差。

4.2 GNSS/SINS组合导航实验

利用GNSS与SINS优势互补的特性，对SPAN-LCI战术级IMU惯导和GNSS采集的车载数据进行基于EKF算法的组合导航解算，得到GNSS/SINS组合导航系统的定位结果，通过与IE解算的结果比较后得到的位置误差、速度误差和姿态误差分别如图6～8所示。

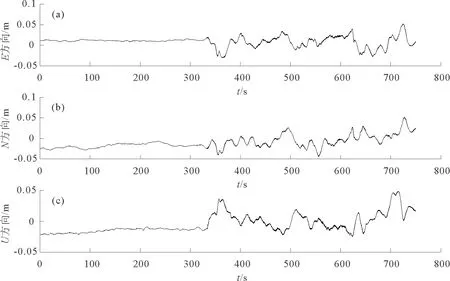
图 6 GNSS/SINS组合导航位置误差Fig. 6 The position error of GNSS/SINS integrated navigation

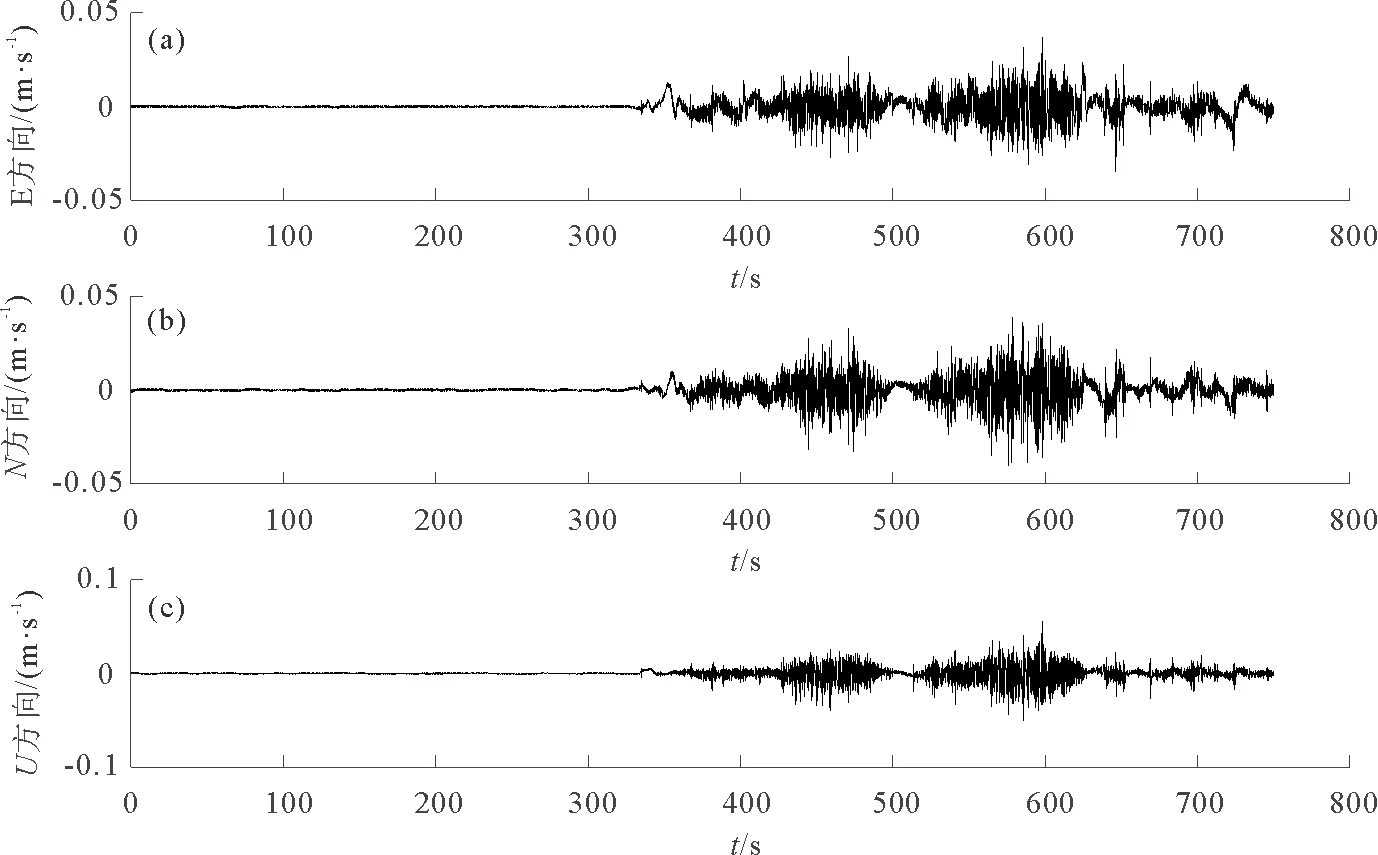
图 7 GNSS/SINS组合导航速度误差Fig. 7 The velocity error of GNSS/SINS integrated navigation

由图6可得，GNSS/SINS组合导航的ENU三个方向的位置误差都收敛了，其中位置误差的精度很高，一直保持在厘米级。通过图6与图3的对比可看出，GNSS/SINS组合导航比SINS单独导航在位置精度方面存在明显优势。由图7得，GNSS/SINS组合导航在E、N两个方向上的速度误差都保持在0.05 m·s-1以内，U方向上的速度误差也保持在0.1 m·s-1以内，与图4相比，GNSS/SINS组合导航的速度误差收敛了，并具有较高的精度。对图8与图5进行对比可以看出，GNSS/SINS组合导航的三种姿态角误差比SINS单独导航时精度稍有提高，其中横滚角误差提高了0.1°左右，俯仰角误差与航向角误差大概提高0.2°左右。尽管GNSS本身不能提供姿态信息，但是SINS与GNSS组合后能得到精度更高的姿态值。

通过对SINS单独导航、GNSS/SINS组合导航的车载实验解算分析可得，基于EKF的GNSS/SINS组合导航算法弥补了GNSS信号失锁、数据更新率低、无法获得姿态信息及SINS误差累积等单系统导航定位中的不足，其能够充分利用两者的优势，得到连续、高数据更新率和高精度的载体导航信息。

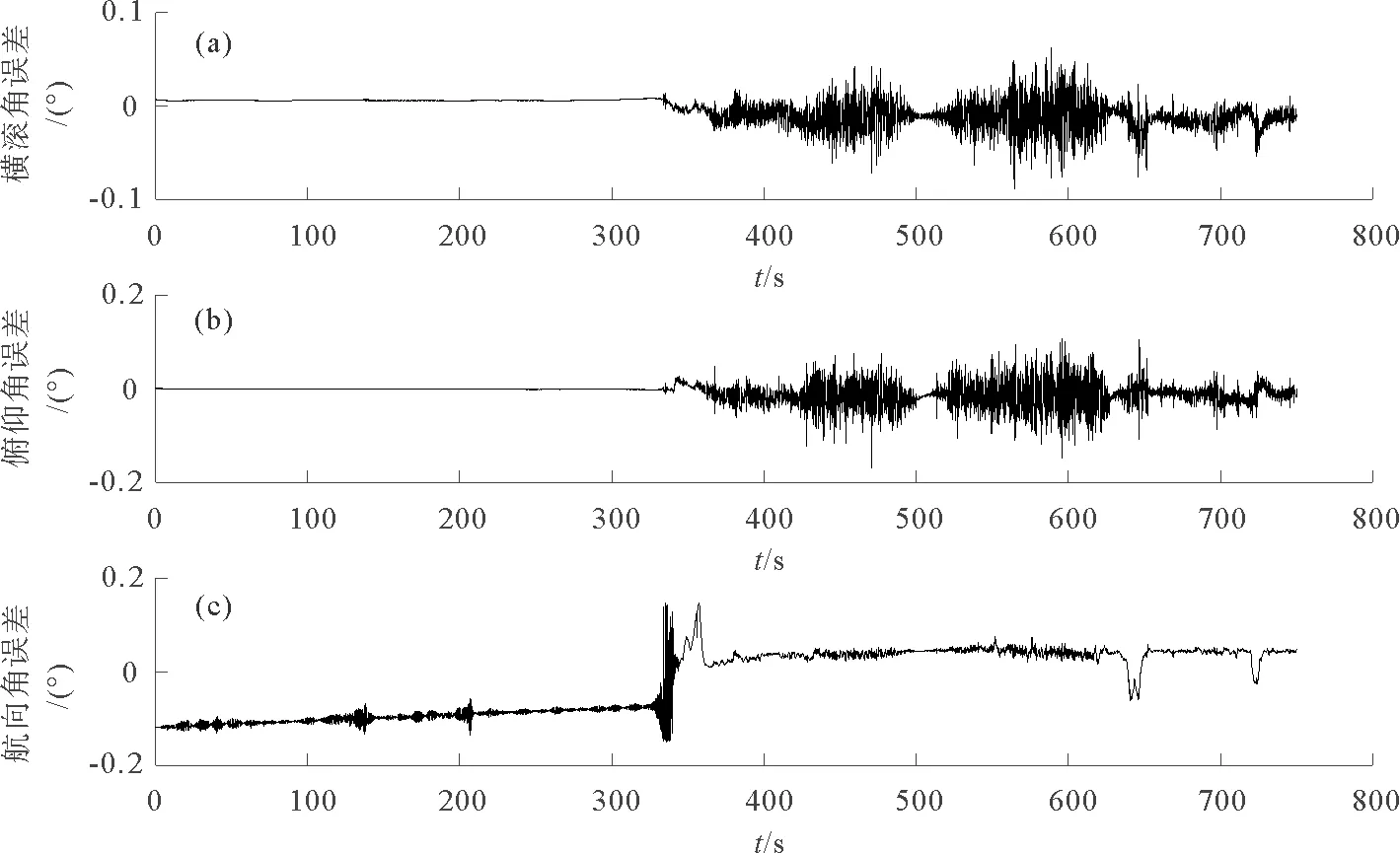
图 8 GNSS/SINS组合导航姿态误差Fig. 8 The attitude error of GNSS/SINS integrated navigation

5 结语

研究了基于EKF的GNSS/SINS组合导航算法，利用GNSS、SINS优势互补的特性，通过EKF算法将两者的定位信息进行融合。首先，研究了SINS、GNSS/SINS以及EKF算法方程，为组合导航算法的实现提供理论基础；其次，实验通过由NovAtel的SPAN-LCI战术级IMU惯导、双系统GNSS(GPS、GLONASS)接收机组成的车载设备进行数据采集，并分别对SINS导航、GNSS/SINS组合导航系统进行解算；最后，将通过自身组合导航算法解算的数据与高精度组合导航后处理软件IE 8.6解算的数据对比，得到GNSS/SINS组合导航解算的位置误差能快速收敛，且精度达到了厘米级，与SINS单独导航系统相比，该组合导航系统具有明显优势。本研究为以后组合导航融合系统的发展提供了一定的实验基础。