基于SPSS的总体比例区间估计教学设计在成人高校统计学教学中的应用

王 波

（北京市东城区职工大学，北京.100061）

在成人高校，统计学的教学一直以来都是令授课教师深感压力较大的一门课程，原因在于统计学的理论基础，尤其是推断统计部分，是概率论，而这个数学基础恰恰是成人学生的短板。统计学的教学常常是在学生几乎不具备这些基础知识的条件下开展的，其难度可想而知。这就需要统计学授课教师在教授那些理论性较强的章节时，花费更多的精力，在考虑学生已有认知以及接受能力条件下，处理、整合、优化教学内容，丰富教学方法与手段，从而激发学生的学习兴趣，使学生能够并愿意接受新知识，达到提高课堂教学效果的目标。本文以总体比例区间估计的教学设计为例，为成人高校统计学相关内容的教学提供一个切实可行的参考。

一、从身边生活实例认识比例及其广泛存在

统计中的比例是指总体（样本）中具有某种属性的单位数与全部单位总数之比的结果，其本质是一个结构相对指标。[1]总体比例可以理解为研究者按照某种标准将总体划分为两个不相交的类别，其中一个类别占总体的百分比。教学中可以从列举大量学生看得见、易于理解的现象入手，使学生理解比例的概念并认识到比例的广泛存在性。例如，将班级全体同学看成一个总体，从性别角度划分总体，从是否戴眼镜的角度划分总体，从单程上班路途所用时间是否超过1个小时划分总体，以及从月平均收入是否超过5000元划分总体等。在这个列举的过程中不但可以使学生进一步认识比例这个概念，同时也能让学生感受到比例是依研究者的目的而确定的，针对同一总体可以构造出多种比例用以研究不同问题。此外，必要时也可以借助集合中的文氏图来帮助学生形象理解比例概念。

二、搞清总体比例与总体均值之间的联系

在计算总体比例时，除了通过统计出总体中具有某种属性的单位数从而计算总体比例外，还可以针对总体重新构造一个与之相关的变量，[2]将总体中属于我们感兴趣的类别的那些个体的对应变量值赋值为1，其余个体对应变量值赋值为0，则赋值后的总体在该变量下可视为0-1分布总体，此时原总体的比例即为赋值后0-1分布总体的均值。同理，原样本比例即为赋值后0-1分布总体的样本均值。

基于上述分析，总体比例的区间估计，可归结为经过赋值重新编码后的总体均值的区间估计问题。若设总体比例为π，样本比例为p，根据中心极限定理，[3]在大样本条件下，样本比例p的抽样分布近似服从均值为π，方差为的正态分布，即其中n为样本容量。于是给定置信水平1-α，由总体均值的置信区间可以得到总体比例的置信区间为，其中为标准正态分布的上分位数。实际求解时由于总体比例π未知，可用样本比例p作为π的估计值，此时所求置信区间为。

以上关于总体比例估计区间的获得过程，不仅可以让学生知道公式的由来，更能使知识间产生联系，能够帮助学生在理解、认识统计概念、公式的同时，体会统计分析方法的使用。事实上，当前很多成人高校和高职高专使用的统计学教材，在介绍总体比例区间估计这部分内容时，往往直接给出估计区间作为公式使用。[1]这虽然避开了繁琐的公式推证，看似符合成人教学特点，然而实际上这种对公式的来龙去脉不加解释显得过于突兀，使学生不愿接纳，也造成了其死记硬背的记忆负担。

三、结合SPSS 统计案例加深概念、方法的认知与理解

理论知识的教学如果不辅以相应的实践往往过于抽象，不容易被理解和掌握，这一点在成人学生身上体现得尤为突出。SPSS是专业的统计软件，其在教学中的优越性体现在无需编程、易于上手，即仅通过菜单操作就可实现绝大部分的统计分析功能，并且分析结果准确、科学、美观。[4]此外更重要的是，SPSS是基于变量及其数据结构的统计分析模式，这种统计分析模式可以让使用者在数据分析过程中，能够全程清晰地关注到变量及其类型，以及变量与变量之间的关系。并且，独立的结果输出窗口，也便于结果的前后对比分析。教学中让学生亲手操作SPSS进行数据分析，可反向促进学生对统计概念、方法、分析过程以及统计思想的理解与把握，[2]从而对于学好统计学提供极大帮助。教学中结合基于SPSS的统计案例，可以使学生在实际动手操作的过程中，逐步体会、消化所学的理论知识，不论对教师的教还是学生的学都大有益处。

案例：某大学为了解学生每周的上网时间，从全校2万名学生中随机抽取100名学生，调查他们一周的上网时间，调查结果如表1所示（单位：小时）。求该校大学生中一周上网时间不小于20小时的比例的95%的置信区间。

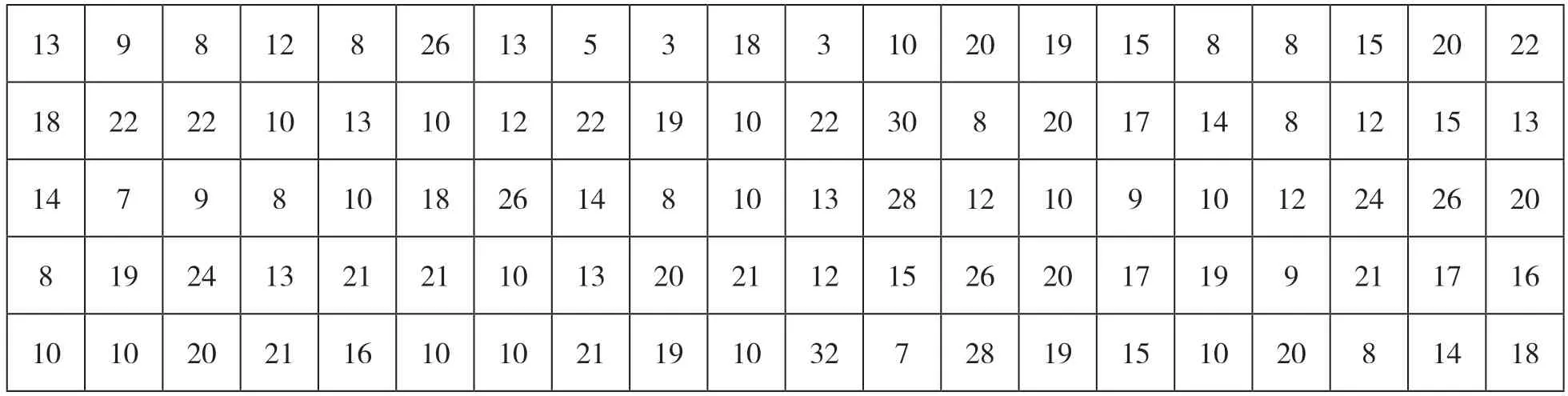
表1 100 名学生的上网时间数据

这里将给出两种解决问题的途径，一种是直接利用前述分析得出区间估计公式，另一种是结合SPSS的上机操作解决问题。教学中，这两种方法的结合能很好地体现既知其然又知其所以然的学习认知过程。

方法一：通过观察或借助Excel对数据进行筛选，统计出上网时间大于、等于20小时的频数为29，进而可得样本比例p=0.29，根据给定的置信水平查标准正态分布表可得，结合总体比例置信区间公式，可得全校大学生一周上网时间不小于20小时的比例的置信区间为：即（20.1%，37.9%）。

方法一属于传统解题法，学生利用已有的总体比例区间估计公式，结合已知条件手工解出此题。动手计算是强化学生接受并运用知识必不可少的过程，但如果仅此而已，学生对统计学的认识仅体现在统计公式的套用上，对统计分析过程、思想与方法的体会是相对肤浅的。

方法二：借助SPSS软件。首先在SPSS中定义变量名称，例如“上网时间”，之后将已知数据录入SPSS中；单击“转换”→“重新编码为不同变量”，在弹出的对话框中，将“上网时间”变量移入右侧“输入变量→输出变量”窗口，定义输出变量名称为“不小于20小时”，单击“更改”，结果如图1所示。再单击“旧值和新值”按钮，在弹出的窗口中，单击左侧“旧值”选项卡中的“范围，从值到最高”，输入20，在右侧的“新值”中输入1，单击“添加”按钮；再单击左侧“所有其他值”按钮，在右侧“新值”中输入0，单击“添加”按钮，结果如图2所示。以上操作实现了将不小于20小时的数据重新编码为“1”，小于20小时的数据编码为“0”。之后单击“继续”→“确定”，在数据视图窗口可以看到重新编码后的变量及其值，如图3所示。

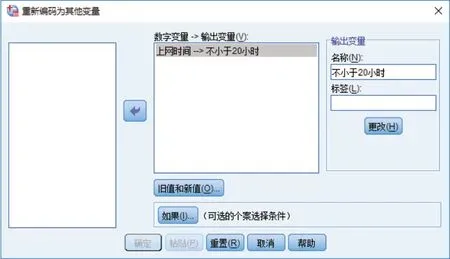
图1 重新编码为其他变量

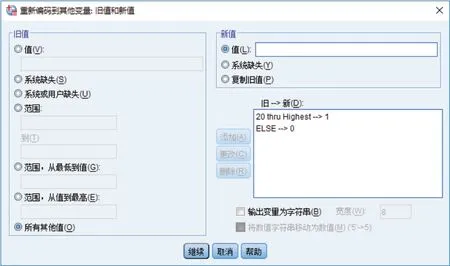
图2 新值与旧值

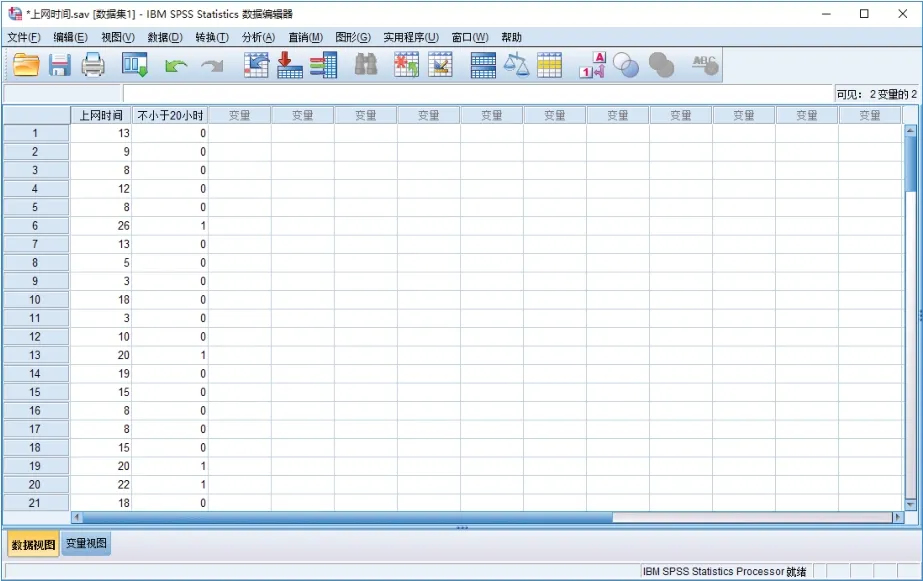
图3 新旧变量及变量值

接下来，在变量视图窗口中，单击“分析”→“描述统计”→“探索”，在弹出的窗口中，将左侧变量“不小于20小时”移入右侧“因变量列表”，如图4所示。单击“统计量”按钮，在弹出的窗口中，勾选“描述性，均值的置信区间”，默认置信水平为95%，如图5所示。单击“继续”→“确定”，运行结果如图6所示。运行结果显示置信下限为0.20，置信上限为0.38，与前者手工计算结果相吻合。

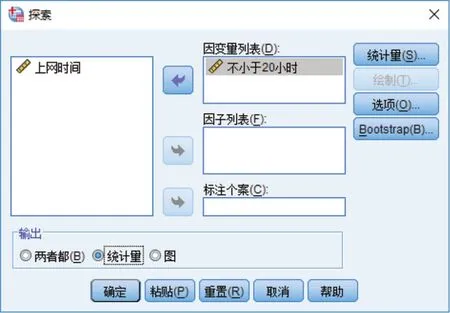
图4 数据探索窗口

图5 探索统计量窗口

图6 运行结果

方法二借助SPSS将样本数据重新编码，实质上是将数值型数据转化为分类数据，即将原上网时间总体转化为0-1分布总体，然后以编码后变量为依据进行总体均值的区间估计，进而得出总体比例的估计区间。在这个动手操作的实践过程中，学生能切实体会到为达到解决问题目的而主动进行的数据类型的转化过程，从而认识到总体比例与0-1分布总体均值的内在一致性，将总体比例与总体均值的区间估计方法联系在一起。这样一个亲自动手分析数据的过程是一次统计分析实践，实践中可以使学生充分体会到转化的统计分析思想、方法，切实感受到总体比例在某种状态下可以理解为总体均值，对统计变量、统计思想、统计方法以及统计分析过程有了更为深刻的认识，有效提高了教学效果。从运行结果上看，SPSS的输出验证了手工计算的结果。这种利用统计分析软件对理论知识的实际验证，也能增进学生对理论知识的认同感。

四、结语

成人高校中，学情永远是课堂教学设计的根本，基础性、理论性较强的统计学教学尤其要考虑学生的认知基础。这就需要成人高校的教师下大力气整合教学内容与教学资源，既要按时完成教学计划任务，又要让学生觉得课堂是有趣、有用和有效的，从而保质保量落实学校的人才培养目标。结合SPSS的统计学案例教学符合成人学生的学习规律与特点，不但有助于其对统计概念、思想、方法的理解，同时也能使看似枯燥的统计理论知识有了实际的用武之地，从而实现学生的学习有获得感、教师的教学有成就感的良好课堂教学效果。