基于Bezier曲线优化的农机自动驾驶避障控制方法

奚小波，史扬杰，单 翔，张 琦，金亦富，龚俊杰，张剑峰，张瑞宏,2※

（1.扬州大学机械工程学院/扬州大学江苏省现代农机农艺融合技术工程中心，扬州225127；2.南京沃杨机械科技有限公司，南京211200）

0 引 言

农机自动驾驶技术是精准农业实施的关键与基础[1-3]，目前农机自动驾驶仪已得到大规模推广使用，尤其在新疆、黑龙江、内蒙等地，农机自动驾驶已广泛应用于耕作、播种、施肥、喷药、收获等农业生产过程[4-7]。现阶段的农机自动驾驶主要以直线驾驶为主，这主要受制于拖拉机动力换挡技术，目前中国一拖集团已成功开发了动力换挡拖拉机，使得农机无人自动驾驶成为新的研究热点[8-9]。

农机在田间作业时可能遇到电线杆、电塔桩、树木等障碍物，需要农机能自动绕过障碍物并迅速回到原有作业路线，因此自动避障是农机无人驾驶的必要技术条件。对于农机自动驾驶过程中的主动避障，一般采取局部路径规划方法，农机在行驶过程中利用传感器获取自身状态信息及周围环境信息，系统监测行驶路径上存在障碍物时，将在短时内提前规划避障路径，并控制农机沿规划路径避障[10-11]。因此，避障路径的规划与控制将直接关系农机能否安全避障、避障精度及避障后直线行驶精度。

现有避障路径规划多采用最短切线法，其具有路径生成快速简单、轨迹短等优点[12-13]，但其路径曲线的曲率不连续且存在折角拐点，易使拖拉机前轮转角骤变，影响农机避障行驶精度。Bezier 曲线是一种连续的平滑曲线，广泛应用于移动机器人轨迹规划、机构运动规划、结构造型等领域，具有曲率连续、控制简单等特点[14-18]。本文以最短切线法为基础，利用Bezier曲线优化避障路径，通过Matlab 仿真研究路径跟踪控制的可行性，并以犁耕作业为例，采用配有动力换挡系统及农机自动驾驶仪的东方红LF954-C型拖拉机研究系统的避障行驶精度。

1 农机运动避障路径规划

1.1 最短切线农机避障路径

在设计农机避障路径前，首先要确认农机前方障碍物特征圆大小及农机与障碍物的距离。为使避障路径容易控制，采用最短切线法规划农机避障路径，如图1 所示，理论避障路径由圆弧段AB、直线段BC、圆弧段CE、直线段EF 和圆弧段FG 组成，其中相邻的圆弧段与直线段相切。根据实际农机作业情况，一般障碍物（电线杆、树木等）轮廓半径小于农机最小转弯半径，因此障碍物特征圆半径R=rmin+0.5l。该避障路径是基于最短切线建立的，通过农机运动几何关系确定各拐点坐标，从而完成避障路径规划，具有快速简单等优点。虽然这种路径在位置和方向上是连续的，但路径曲线的曲率不连续，致使农机运动角速度不连续，农机在由圆弧段转直线段（或直线段转圆弧段）时其前轮转角骤变且变幅较大，难以实现快速调节，从而无法保证农机沿既定路径行驶，影响农机避障的行驶精度。

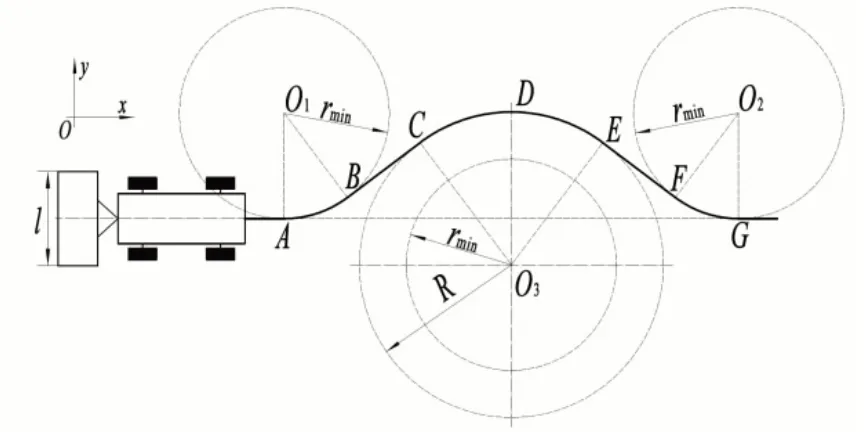
图1 最短切线避障轨迹图Fig.1 Trace of shortest tangent obstacle avoidance path

1.2 Bezier曲线避障路径优化

给定空间n+1 个控制点Pi（i=0,1,···,n），则Bezier 曲线方程可表示为[19-20]：

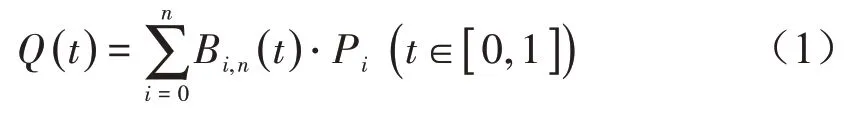
式中t 为位置参数，Bi,n(t)是n 次Bernstein 基函数。对Bezier曲线方程求导得：

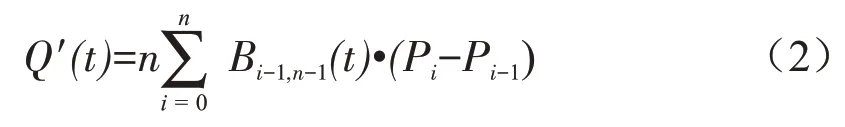
将t=0与t=1带入公式（2），则有：

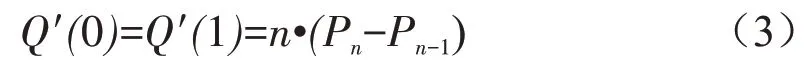
式（3）说明，Bezier 曲线在起点和终点处的切线方向与控制多边形第一条边和最后一条边的走向一致。因此，通过规划Bezier曲线起点和终点的切线方向，即可实现对农机初始位姿和目标位姿的确定，有利于农机避障完成后继续沿初始姿态行驶。

本文采用Bezier曲线对最短切线规划路径作进一步优化，以期形成曲率连续的光滑路径。依据最短切线避障路径可知，农机在避障过程中有A、B、C、D、E、F、G 共计7 个控制点，理论上可采用六阶Bezier 曲线，为降低Bezier 曲线复杂性，且基于原避障路径的对称性，采用2段三阶Bezier 曲线，即A、B、C、D 为前半段，D、E、F、G 为后半段。同时采用2 段三阶Bezier 曲线替代六阶Bezier曲线，可有效避免因Bezier 曲线凸包性[21]造成的避障曲线与实际控制点的相对偏差过大造成避障任务失败。三阶Bezier曲线为三次多项式，其矩阵为[22]：

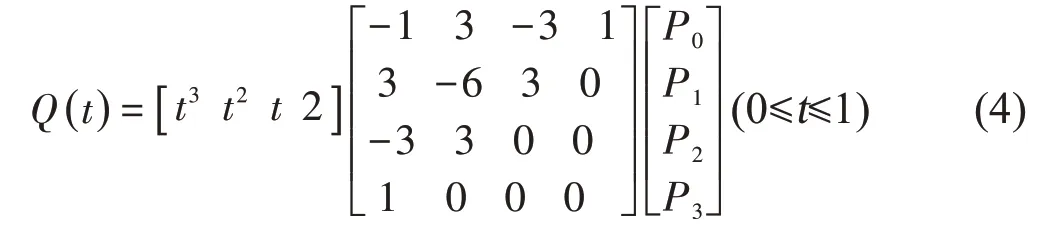
则有

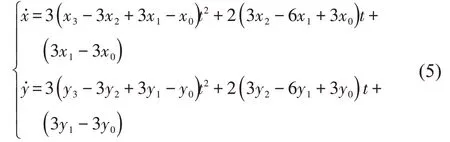
式中x0、x1、x2、x3分别为P0、P1、P2、P3的横坐标，cm；y0、y1、y2、y3分别为P0、P1、P2、P3的纵坐标，cm。

以东方红LF954-C 拖拉机为例，农具以250 cm 幅宽犁为例（与下文试验一致），根据该型拖拉机技术参数得出控制点的相对坐标（单位：cm）：A（333.28, 0）、B（501.47,56.22）、C（694.94,201.43）、D（938.50,282.85）、E（1182.06,201.43）、F（1375.52,56.22）、G（1543.71,0）。在Matlab中对上述坐标进行2段Bezier曲线创建，如图2所示，可以看出，该路径存在显著拐点，如点A、D、G，且起始点A与目标点G的走向并不一致。造成上述现象的原因是，控制点分布的离散性较小，致使拟合成的Bezier曲线过于线性，为此需要作进一步优化调整。

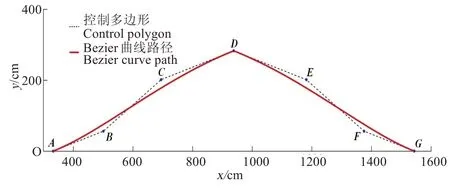
图2 最短切线避障路径控制点生成的Bezier曲线Fig.2 Bezier curve generated by control points on shortest tangent obstacle avoidance path

为增大控制点的离散性且不改变Bezier 曲线的走势，将控制点B、C、E、F 分别向曲线两侧拉伸。为保证整段曲线起点与终点的走向一致，需使前段曲线终点与后段曲线起点的走向一致，优化调整后控制点的相对坐标（单位：cm）：A（333.28, 0）、B（1635.89, 0）、C（1635.89,282.85）、D（938.50, 282.85）、E（11241.105, 282.85）、F1（1241.105,0）、G（1543.71,0），新生成的Bezier 曲线如图3 所示。通过上述方法可提高整段曲线对称性，其每段曲线呈中心对称，整段曲线呈轴对称。

一般参数方程曲线的曲率c为[23]

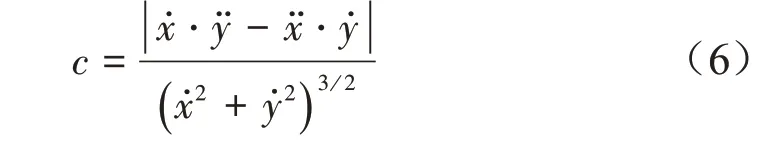
对式（5）进一步求导并将各点坐标值代入式（6），求得前段曲线AD 的终点曲率与后端曲线DG 的起点曲率一致，说明上述整段避障路径AG 的曲率连续，农机沿着该曲线行走容易控制。

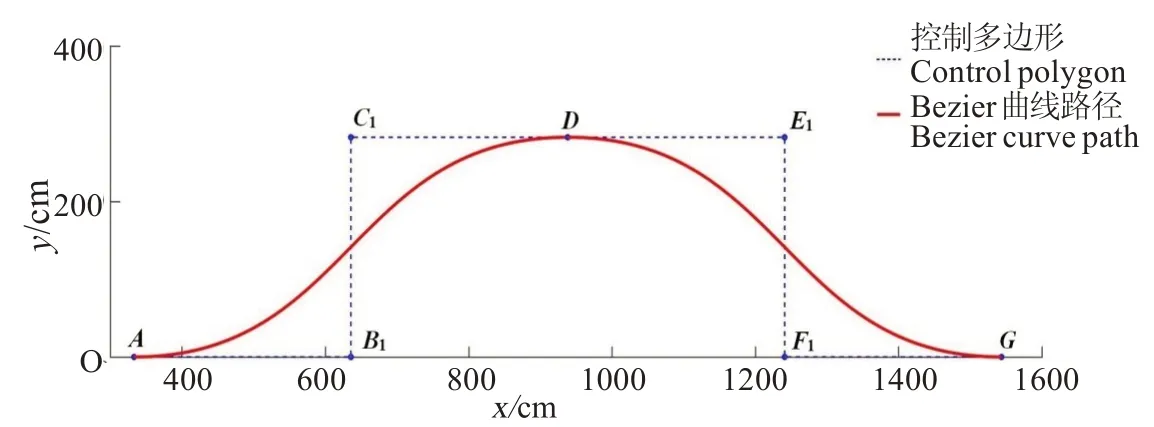
图3 优化控制点生成的Bezier曲线Fig.3 Bezier curve generated by optimized control points

2 农机运动控制方法

2.1 农机运动模型

本文研究的避障控制方法主要针对轮式拖拉机，鉴于农机作业的低速性，将四轮拖拉机简化成二轮车模型进行运动学分析[24]，如图4 所示。规定当农机控制点N沿曲线顺时针运动时的曲率c 为负，逆时针运动时c 为正；当控制点N 在曲线外侧时的横向位置误差d 为正，在曲线内侧时d为负。

为简化农机运动模型建立过程，需作如下假设[25]：一、农机与农机具是一个独立刚体，即农机运动时只有一个瞬时旋转中心；二、农机运动为纯滚动而非滑动，即农机的运动速度方向沿着车身中心线方向。一般农机具与农机的连接为三点悬挂连接，该连接方式基本不会滑移窜动，符合刚性连接条件。同时，农机作业工况相对平坦，符合滚动运动条件。基于上述假设，则有[26-27]：

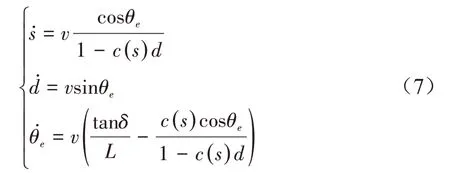
式中c(s)为M点处的路径曲率。有2种情况使方程（7）不成立，一是当d=1/c(s)时，即农机与路径间的位置误差等于路径曲线的半径，依据农机自动驾驶仪的相关标准规定，导航作业精度为±2.5 cm，说明农机与路径间的位置误差为厘米级，而拖拉机的转弯半径一般为米级，因此d=1/c(s)的种情况不会发生；二是θe为直角的倍数，即农机行驶方向与路径方向垂直，这显然不符实际。因此，方程（7）的农机运动模型成立。

2.2 农机运动控制

通过上述方法建立的农机运动模型是一种高度的非线性模型，为了应用线性系统控制方法，采用链式控制理论将非线性模型转化成近似线性模型，通用链式系统一般为三状态两输出系统，其表达式如下[28]：

设Q=(a1,a2,a3)T表示系统状态变量，U=(m1,m2)T表示系统控制变量，为使方程（8）线性化，只需用状态变量a1的导数替换时间导数，令：

则方程（9）可以表达成：

显然，方程（10）为线性方程。令a1=s，a2=d，则变量m1、m2与a3可表达成：

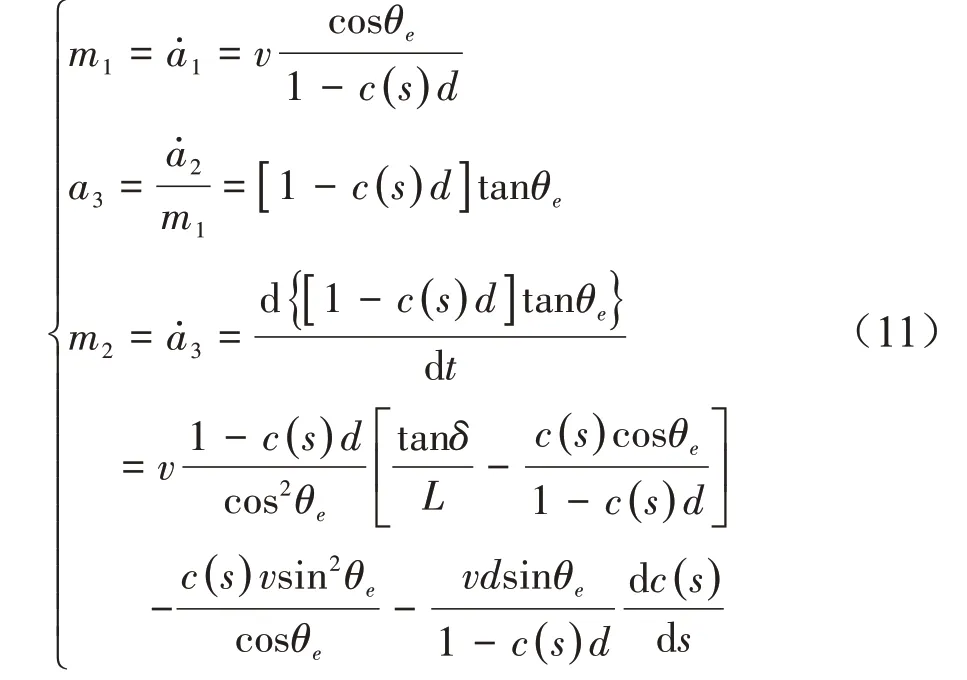
因为方程（10）是线性系统，可采用状态反馈控制方法对系统进行控制[29]，令：

式中控制参数(K1,K2)∈R+。将方程（12）带入方程（10）中得控制律：

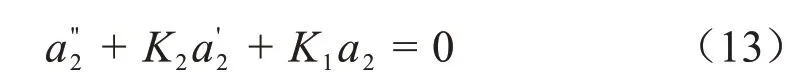
上述控制律是为了控制a2和a3趋近于0，同样可用来控制d 和θe趋近于0，从而达到农机路径曲线的跟踪控制。联立方程（13）与（11）可以得到实际的农机前轮转角控制律δ(d,θe)为：

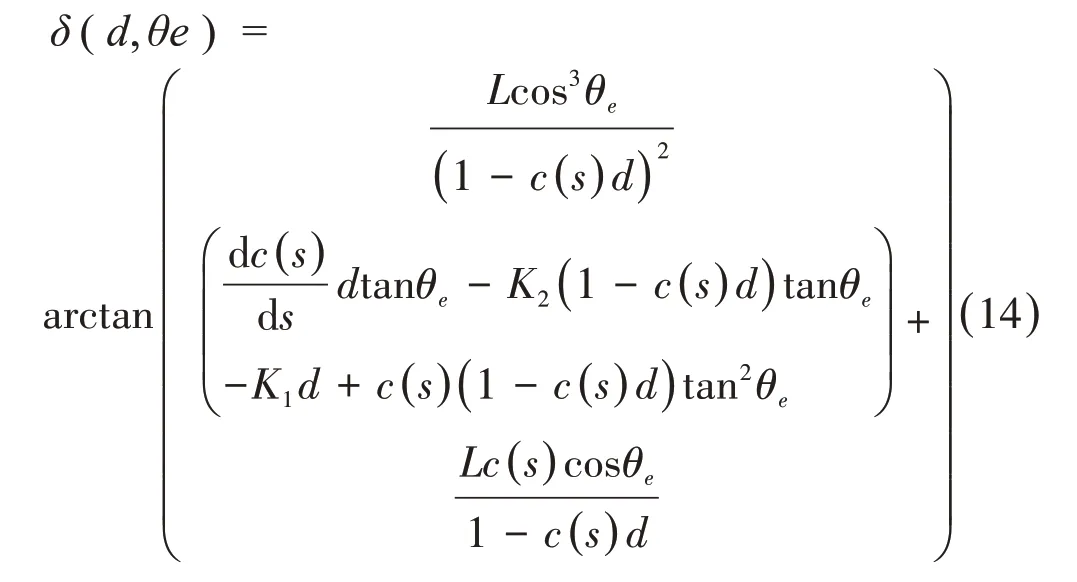
由于农机运动模型的精确度直接影响路径跟踪的控制质量，且随着路径曲率的增大，运动模型的精确度也会下降，控制性能将会降低。本文采用链式控制器得到理论前轮转向角δ(d,θe)后，利用PI控制器解算出期望转向补偿角δc，将δ(d,θe)与δc相加后得到农机实际转向角δt，并输出给农机模型，控制农机沿路径行走。

传统PI控制器的控制律[30]：

式中，u(k)为PI 控制的输出，Kp为比例增益，Ki为积分增益，e(i)为i 时间对应误差输入，k 为总采样时间点数。计算时，将农机航向误差角θe作为PI 的误差输入，则当前期望转向补偿角δc即为u(k)。

3 仿真分析

采用Matlab 对农机运动的航向误差角、横向位置误差及前轮转向角情况进行了仿真分析。农机选用东方红LF954-C，轴距231.4 cm，前轮转角范围（-π/6,π/6），最小转弯半径5.6 m，配套农机具幅宽250 cm。依据Bezier曲线优后的路径建立轨迹约束模型（图3），按照仿真设计描述在Matlab 软件编程实现预设轨迹并建立路径跟踪仿真模型，设定农机起始位置坐标为（333.28, 0）（单位：cm），初始前轮转角为0，农机运动速度1 m/s，选取理论前轮转向角控制参数K1=0.09，K2=0.6，选取期望转向补偿角控制参数Kp=2，Ki=0.01。

图5 为农机避障运动仿真结果。由图5a 可知，农机的跟踪轨迹与预设轨迹基本重合，说明本控制方法具有较高的路径跟踪精度。由图5c 可以看出，农机行驶的航向误差角在-0.06～0.06 rad 范围内，其数值较大点主要分布于路径轨迹曲线斜率较大位置处，这是由于此处采样点比较稀疏，导致M 点相对较少，但在实际运行时采样点比较密集。从图5b 可以看出，农机行驶的横向位置误差在13 cm 内，能符合农机曲线避障行驶要求。从图5d 可以看出，前轮转向角δ 变化平缓，总体上由0 逐渐增大，后又减小至0，然后变为负值继续增大（δ 负值表示农机沿顺时针转弯行驶、δ 正值表示农机沿逆时针转弯行驶），呈周期变化，与农机实际转弯过程相符，整个运动曲线中过程δ 没有显著突变，这有利于控制器对期望角度的跟踪。上述结果显示，通过本控制方法进行的农机避障路径跟踪控制，其控制精度高，农机基本按照预设轨迹行驶。

图5 农机避障运动仿真结果Fig.5 Simulation results of tractor obstacle avoidance movement

4 避障精度试验

4.1 试验过程

拖拉机选用东方红LF954-C 型，农具选用250 cm 幅宽犁。拖拉机安装北斗农机自动驾驶仪（南京沃杨KM-502，直线行驶精度±2.5 cm），并通过超声波雷达、图像识别技术实现作业环境的障碍物感知。该型拖拉机配有动力换挡装置，可进行自动启停、换挡、农具升降操作。试验在无锡卡尔曼导航技术公司的导航试验基地进行，场地平坦，设置草堆障碍物，其轮廓半径约3 m（小于拖拉机最小转弯半径），障碍物特征圆半径R=rmin+0.5l=6.85 m。拖拉机一档行进（约3.6 km/h），犁耕深度25 cm，整机工作时，通过超声波雷达与视觉机器识别障碍物信息，通过拖拉机位置传感器计算避障安全距离，并规划避障路径轨迹，拖拉机在北斗农机自动驾驶仪的控制下按照预设轨迹路径完成自动避障过程。

对机具避障精度进行了试验，在拖拉机车身中心线上安装高精度卫星接收机，即RTK 测量仪，测量精度0.01 cm。由于RTK 测量仪系统内难以设置Bezier曲线，设置测量基准线为直线A'B'，通过卫星接收机记录的RTK 位置数据xi（监测点至A'B'的距离）减去理论避障路径至A'B'的距离，得到监测点与理论避障曲线的误差值hi（取正），如图6所示。

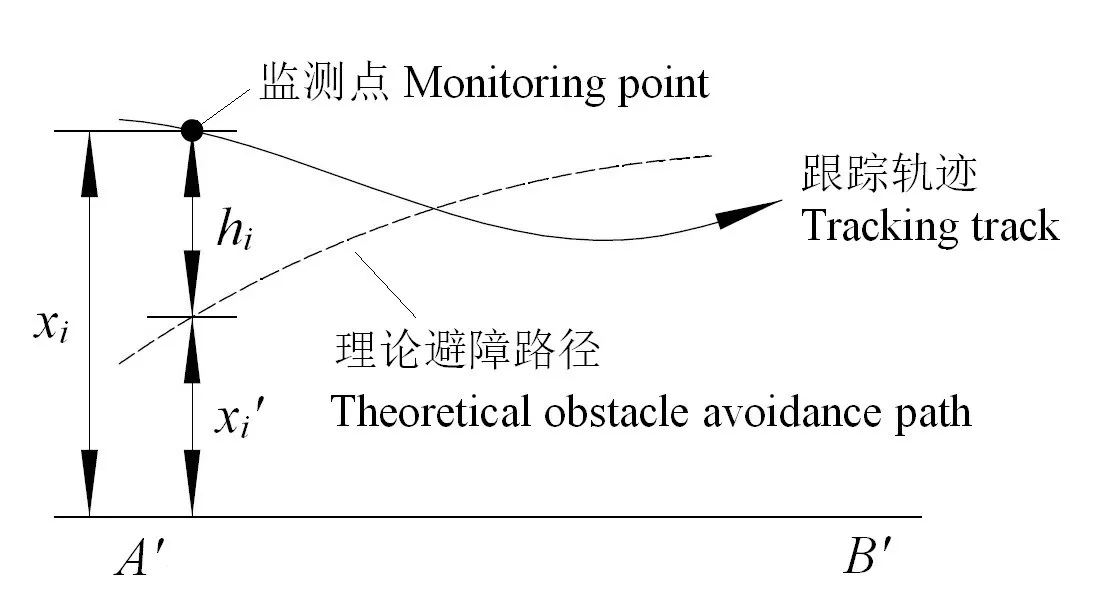
图6 避障精度测试示意图Fig.6 Schematic diagram of obstacle avoidance accuracy test

通过公式（16）计算得出跟踪轨迹与理论避障曲线的标准差，该标准差即为避障精度，标准差越大，表示该避障跟踪精度越差[31]。

4.2 试验结果与分析

避障精度测试分2 个部分，第一部分为避障曲线部分（Bezier 曲线起点至终点），第二部分为避障后继续沿直线行驶部分。每监测点相距100 cm，由于障碍物特征圆半径为6.85 m，因此前13 个监测点为避障曲线位置点，直线行驶部分亦取13点，共计26个监测点，结果见表1。

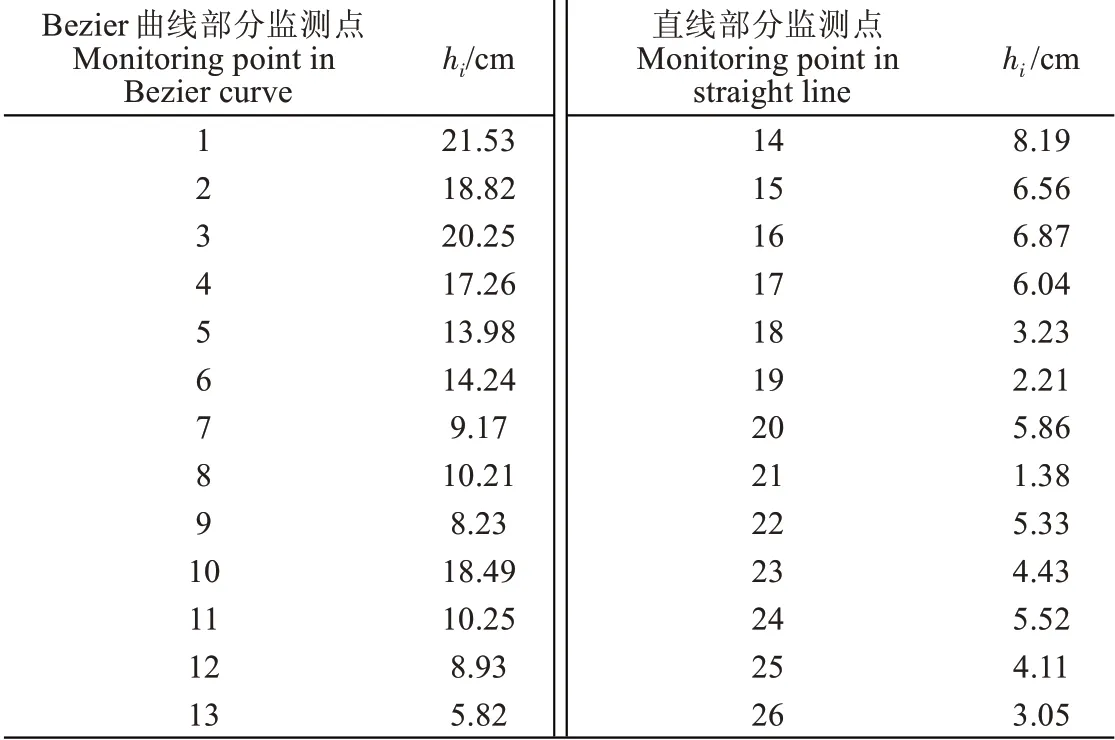
表1 监测点到理论避障曲线的距离Table1 Distance from monitoring point to theoretical obstacle avoidance curve

根据表1 数据，通过公式（16）求得曲线部分的监测点到理论避障曲线的误差平均值为13.63cm，标准差为5.21cm，曲线起始部分的误差较大，最大误差达21.53 cm，主要是因为犁耕作业时拖拉机前进方向的左侧轮胎置于耕地中行驶，拖拉机处于一边倾斜状态，避障时拖拉机则又驶入平地，行驶工况的变化导致避障精度的稳定性有波动，同样从平地进入耕地时，直线行驶精度的稳定性也会有所波动。上述结果显示，曲线部分的避障精度为5.21 cm，说明本文设计的避障曲线及控制方法具有较高的避障精度，曲线路径的跟踪控制效果较好，在不平整的犁耕地中表现出较好的鲁棒性和适应性，可满足拖拉机作业的避障要求。同时，避障后农机继续沿直线行驶的监测点到理论轨迹的误差平均值为4.83 cm，标准差为1.98 cm，即避障后农机继续沿直线行驶的精度为1.98 cm，说明本文设计的路径跟踪控制方法可保证农机在避障后恢复直线自动驾驶。

本文设计的避障路径规划与控制方法也可适用于拖拉机田间调头作业，可为农机全程无人化自动驾驶提供技术依据。

5 结论

1）本文通过2 段三阶Bezier 曲线优化了农机避障路径，优化后的曲线曲率连续，避障路径平滑无拐点，利于农机行走控制。针对农机运动模型精度低的问题，通过链式控制理论建立农机运动的线性控制模型，利用PI 控制器进行转角补偿，提高农机避障行驶精度。

2）仿真结果显示，农机行驶的航向误差角在-0.06～0.06 rad范围内，横向位置误差小于13 cm，前轮转向角变化平缓，没有显著突变，说明该避障路径控制方法的控制精度高，农机能按预设轨迹行驶。

3）犁耕作业试验结果显示：Bezier 曲线部分的避障精度为5.21 cm，曲线路径的跟踪控制效果较好；避障后农机继续沿直线行驶的精度为1.98 cm，说明该路径跟踪控制方法可保证农机在避障后恢复直线自动驾驶。上述结果表明，该避障路径及控制方法在不平整的犁耕地中表现出较好的鲁棒性和适应性，可满足拖拉机作业的避障要求。