GNSS RTK高程拟合控制点选取工具设计与实现

林春峰

(中铁二院工程集团有限责任公司，成都 610031)

1 概述

在铁路工程项目勘测阶段，一般采用GNSS RTK测量方法进行外业数据采集，能够实时获取待测目标与基站差分之后的BLH坐标；然后，通过控制点计算得到平面和高程坐标转换参数，再分别进行平面坐标和高程转换，得到工程项目所需的投影坐标和正常高[1]。已有许多学者进行相关研究，李婉清等认为，实现低成本终端的高精度定位受其接收机信号处理能力，以及由天线性能引起的相位中心误差、多径误差等问题制约[2]；黄甜对GNSS RTK控制测量的精度进行实验，发现平面位置的点位误差在5 cm左右[3]；史永明从原理、算法上对GNSS高程拟合进行阐述[4]。不难看出，平面转换精度与控制点的选取关系不大，但高程拟合精度却与控制点数量、位置分布等影响因素紧密相关[5]。在使用GNSS RTK进行工程测量前，如何快速选取合适的控制点用于高程拟合鲜有研究，以“小范围作业区内采用平面函数模型[6]进行高程拟合”为原则、“地理学第一定律”为依据[7-9]，提出一种利用控制点空间位置关系、高程异常值、高程不符值和东北斜坡值为参考依据进行控制点选取的方法，并基于某西南山区旅游铁路项目，以证明提出方法的可靠性。

2 GNSS高程拟合原理分析

一般情况下，大地高不能取代实际工程中所采用的高程(正常高)，但可以通过确定地面点高程异常来实现大地高与正常高之间的转换。高程异常ζ、大地高H和正常高h之间的关系为ζ=H-h。因此，GNSS高程拟合的核心问题就是确定高程异常[10-12]。

在进行GNSS高程拟合计算前，需少量的已知控制点。假设已知控制点为

GNSS RTK测量中，在小范围内，通常利用平面函数模型建立高程转换参数[13]，其数学公式为

f(Δx，Δy)=a×Δx+b×Δy+c

(1)

式中，f(Δx，Δy)为控制点或者待计算点高程异常值与起算点高程异常的差值；Δx为当前控制点或待计算点与起算点投影北坐标差值；Δy为当前控制点或待计算点与起算点投影北坐标差值；a、b、c为待求解的参数。

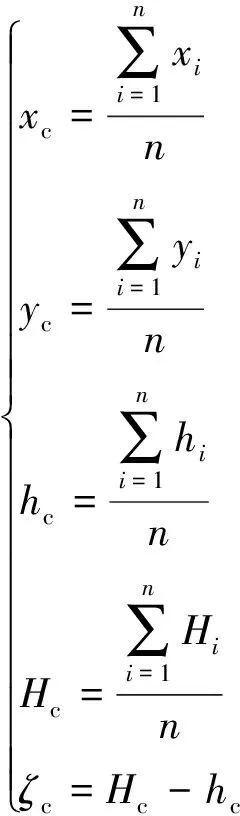
(2)

再计算控制点与起算点的北、东坐标差、高程异常值之差，即

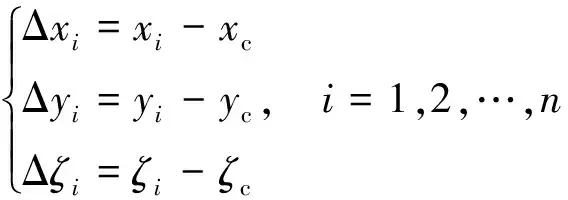
(3)

可利用平面函数模型列出计算公式，有

Δζi=a×Δxi+b×Δyi，i=1，2，…，n

(4)

将上述公式变换成矩阵形式，有

(5)

利用最小二乘可计算出a和b。其中，a为东斜坡参数；b为北斜坡参数。

待计算点高程异常值ζT=ζc+ΔζT；

待计算点正常高hT=HT-ζT。

3 工具设计与实现

采用该GNSS RTK高程拟合控制点选取工具，可导入控制点数据和线位文件，显示控制点空间位置分布、高程异常值曲线、高程不符值曲线，以及计算GNSS高程拟合参数、待求点正常高等。软件工具逻辑流程见图1。软件主界面见图2。

图1 软件工具逻辑流程

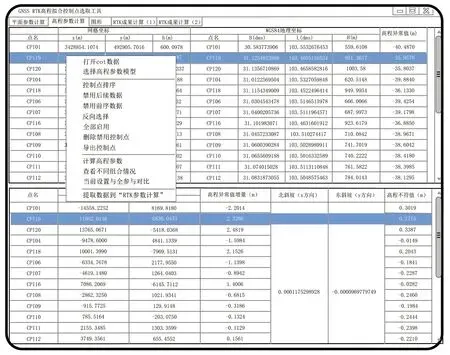
图2 软件工具主界面

首先，导入控制点，工程图形界面可以显示控制点分布，见图3。图3中的连接线按照控制点排序进行连接绘制，后续选择控制点进行拟合参数计算后，高程异常值分布和高程不符值分布都将按照导入的控制点次序进行绘制。按照地理学第一定律，可人为指定第一个控制点，然后，按照空间距离依次进行排序，再进行拟合参数计算、绘制高程异常值分布和高程不符值分布(见图4、图5)。最后，从图形中发现规律，以选取合适的控制点。

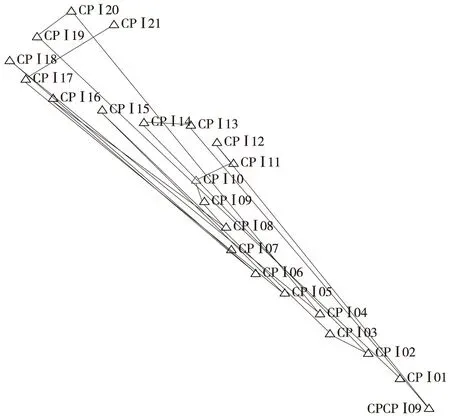
图3 控制点分布(任意排序)

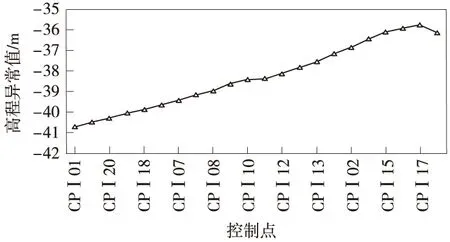
图4 高程异常值分布(任意排序)

图5 高程不符值分布(任意排序)

4 实验分析

某西南山区旅游铁路项目线路长约35 km，共获取22个控制点，现需选取部分控制点用于GNSS RTK高程拟合计算。首先导入全部控制点，并进行排序、计算，绘制控制点分布和高程异常值分布，见图6、图7。

图6 控制点分布(顺序排序)

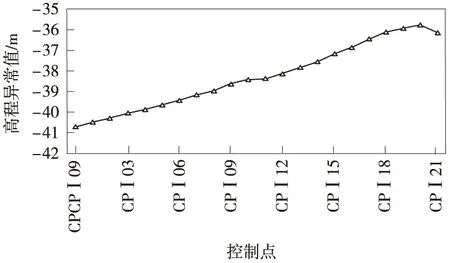
图7 高程异常值分布(顺序排序)

按照式(2)、式(3)，得到控制点Δx、Δy和Δζ数值，见表1。

表1 控制点计算结果 m

并按式(5)进行参数计算，可以得到a=0.000 117 529 893；b=-0.000 096 977 975；各点的高程不符值。高程不符值分布见图8。

图8 高程不符值分布(顺序排序)

由表1、图8可知： (1)控制点高程异常值曲线较为平缓，排序后相邻控制点的高程异常值变化趋势一致；(2)将所有控制点进行高程拟合计算，各点高程不符值均过大；(3)控制点高程不符值分布曲线较为平缓，高程不符值先平缓降低，然后保持不变，最后平缓增加；(4)北斜坡和东斜坡数值表明，各控制点高程异常值与起算点高程异常的差值拟合的平面呈现“东南低、西北高”等特点。

因此，需将控制点进行分段。顾及高程异常值变化趋势，可先根据高程不符值分布进行控制点分段(见图9)。

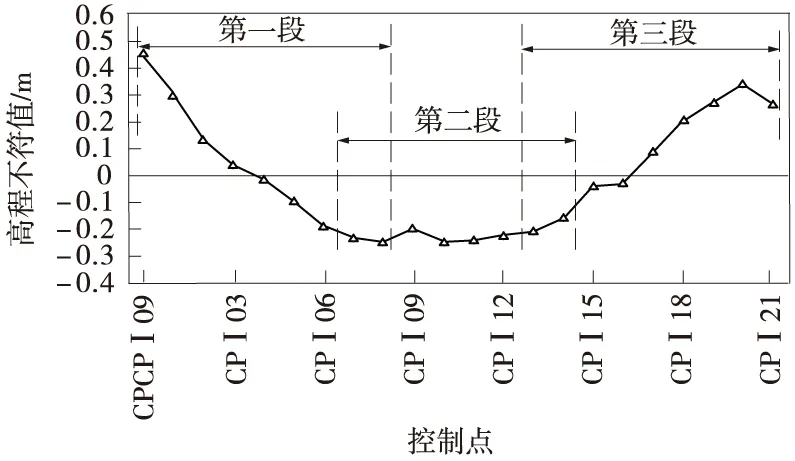
图9 控制点分段示意

分别计算每个区段的拟合参数，得到高程拟合统计，如表2所示。

表2 高程拟合计算结果

由表2可知： (1)各段高程不符值均较小，满足GNSS RTK高程拟合精度要求；(2)各段控制点高程异常值与起算点高程异常差值的拟合平面呈现“东南低、西北高”等特点，与使用EGM2008[15]等重力场模型绘制的高程异常区曲线相吻合[16]。

分别导入每一段选择的控制点，利用“查看不同组合情况”功能，选组合点个数(见图10)，设置启用点和禁用点(见图11)，表格中标记为红色的点可以当做检核点。计算不同组合的拟合参数，并绘制高程不符值曲线，如图12所示。

图10 选择组合点个数

图11 不同组合情况计算结果

图12 不同组合情况的高程不符值分布

由图12可知：(1)所有组合高程不符值曲线与利用全部点计算的高程不符值曲线变化趋势一致； (2)有两个组合高程不符值大于0.10 m、小于0.15 m，其原因为未将起点和终点控制点纳入计算； (3)其余各组合中各点高程不符值均小于0.10 m。

利用“查看不同组合情况”功能，在第一段中设置启用点和禁用点(检核点)进行计算。检核点高程不符值均满足GNSS RTK高程拟合精度要求。因此，可以判定第一段分段合理。

按照上述流程继续判定第二段、第三段，亦可得出“分段合理”的结论。

5 结语

提出一种利用控制点空间位置关系、高程异常值、高程不符值和东北斜坡值为参考依据进行控制点选取的方法，并开发相关工具，提高了高程拟合的数据质量。实践表明，用于GNSS RTK高程拟合所选取的控制点需覆盖作业区，否则其拟合精度不可靠；依据“地理学第一定律”和平面函数模型的特点，所选择的控制点范围不宜过大；相邻作业区存在共用控制点，需检核、判断共用控制点在不同作业区内的高程异常值是否满足高程拟合精度。下一阶段，可在不同的高程拟合模型、结合EGM2008等重力异常数据进行高程拟合等方面进行研究，进一步完善该工具。