垂线偏差对高原艰险铁路长大隧道平面控制测量的影响

王不悔 刘成龙 许双安 武瑞宏 杨雪峰 何金学

(1.西南交通大学地球科学与环境工程学院，成都 611756； 2.西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室，成都 6117563； 3.中铁第一勘察设计院集团有限公司，西安 710043)

1 概述

1.1 研究意义

川藏铁路全长约1 800 km，东起成都，经雅安、康定、昌都、林芝至拉萨，是铁路工程设计与建设的世界级难题[1]。川藏地区的地形地貌极其复杂多变，全线桥隧占比超过80%，其中隧道总长度达1 200 km[2]。因此，隧道在川藏铁路中占有重要的地位，而建立精确、可靠的隧道测量控制网，是川藏铁路长大隧道顺利贯通的基本前提。

依据地球重力场模型EGM2008，在高海拔地区极端情况下垂线偏差改正数理论上可达±50″[3]，而高海拔、大高差会给川藏铁路高精度隧道平面控制网的建立带来诸多不利影响，进而导致川藏铁路长大隧道无法顺利贯通。因此，在川藏高原地区进行隧道洞内外平面控制网测量实验，并研究垂线偏差对川藏铁路长大隧道平面控制网的影响情况，对川藏铁路建设具有重要意义。

1.2 垂线偏差对高原地区长大隧道控制测量的影响分析及其实验网的布设

现阶段，绝大部分隧道洞外平面控制网的建立，均通过GNSS相对定位测量方法完成，由于GNSS测量的基准面为参考椭球面，故隧道洞外控制网不受垂线偏差影响[4]。而在垂线偏差显著的地区，隧道洞内边角控制网测量及进洞联系测量中，全站仪测量的观测边水平方向观测值易受垂线偏差的影响。

根据垂线偏差对全站仪水平方向观测值的改正数δ计算公式为[5]

δ″=-(ξ″sinA-η″cosA)cotZ

(1)

式中，ξ、η分别为测区的垂线偏差在子午圈和卯酉圈上的分量；A为测站点至照准点的大地方位角；Z为测站点至照准点的天顶距。

由式(1)可知，当测站点到观测点间高差不大时，无论测区垂线偏差值如何，其观测边的水平方向观测值几乎不受垂线偏差影响。高差越大，其水平方向观测值受到测区垂线偏差的影响则越明显。对于铁路隧道，由于其洞内纵向设计坡度不大，故受垂线偏差影响较小。而位于高原峡谷处的隧道洞口，进洞后视点与进洞联系点间的高差一般较大，故进洞联系测量后视边(以下统称为进洞后视边)的水平方向观测值受到垂线偏差影响较大。因此，测区垂线偏差对隧道洞内观测边水平方向观测值的影响较小，其主要影响进洞后视边的水平方向观测值，进而影响洞内平面控制网的最终横向精度。

为研究高原地区垂线偏差对隧道平面控制测量的影响情况，在海拔高程为4 300 m的川藏铁路高原地区，模拟布设1条隧道洞内外平面控制测量实验网，并对控制网中各点进行高精度GNSS静态相对定位测量与全站仪边角网测量。实验网布设于西藏昌都川藏铁路线位附近，全长约13 km，并每隔400 m左右布设1个洞内控制点，所有控制点均为强制观测墩。在模拟的隧道进出洞口各布设3个洞外控制点，其中1个为进洞联系测量点，其余2个为进洞联系测量的后视点。实验网网形设计为隧道洞内附合单导线控制网，如图1所示。

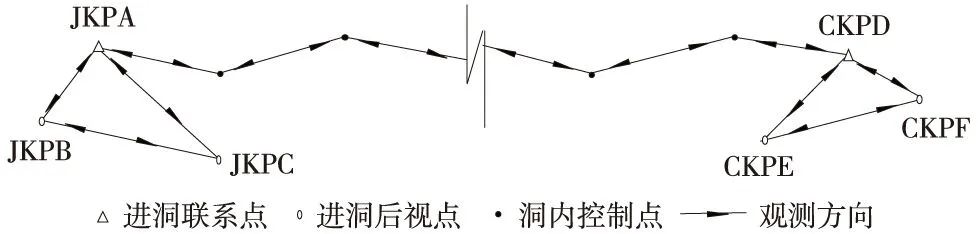
图1 实验网网形示意

图1中，JKPA与CKPD为洞外的进洞联系测量点，JKPB、JKPC、CKPE与CKPF为洞外的进洞联系测量后视点。为反映川藏地区垂线偏差对进洞后视边水平方向观测值真实的影响程度，实验网布设时，人为将进洞联系测量测站点和后视点选择在高差较大的地方。洞口控制点的具体布设情况如下：出洞处进洞联系点CKPD到后视点CKPF间的距离为480 m，仰角约19°；与另一个洞外后视点CKPE间的距离为630 m，仰角约12°，进洞处洞外控制点布设与出洞处类似。

2 实验网外业观测及其精度情况

2.1 外业测量方法及等级要求

为确保实验数据的准确和能够突显垂线偏差的影响，实验网中GNSS静态相对定位外业测量严格按照《全球定位系统(GPS)测量规范》中C级网外业测量的技术要求执行，附合单导线网的外业测量严格按照二等导线网的技术要求执行。

2.2 GNSS测量数据处理

首先，对实验网的GNSS外业观测数据进行整网基线解算，并按照规范要求进行基线质量的检核统计，具体统计结果如下。

(1)重复基线较差检验

全网中共有重复基线156条，所有重复基线边的长度及其分量较差均满足其限差要求，重复基线较差最大的基线较差信息统计结果见表1。

表1 重复基线最大较差统计 m

(2)独立闭合环环闭合差检验

全网中共组成123个独立闭合环，各闭合环的X、Y、Z方向和全长绝对闭合差，也均满足其相应的限差要求，最大闭合差的独立闭合环相关信息统计结果见表2。

表2 独立闭合环最大闭合差统计 m

从上述基线解算后统计的两项指标结果可知，实验网的GNSS外业数据质量检核合格。故可以把解算后的所有基线叠加在一起，进行三维无约束平差。根据相关规范，要求GNSS网三维无约束平差后基线向量各分量的改正数的绝对值(VΔX、VΔY、VΔZ)，应满足式(2)要求，即

VΔX<2σ、VΔY<2σ、VΔZ<2σ

(2)

式中，σ为基线长度中误差。实验网三维无约束平差后的三维基线向量改正数最大值(分量改正数最大值并不是出现在同一条基线中)的统计结果见表3。

表3 三维无约束平差基线向量各分量的改正数最大值 cm

由上述内容可以看出，本次实验网中的GNSS基线向量自身的内符合精度较高，基线向量质量可靠，满足相关规范要求，能够达到设计的实验精度要求。

2.3 附合单导线网外业数据处理与检验

按照规定的测回数和测站限差要求，完成实验网中全站仪附合单导线外业测量数据采集后，先对测得的距离观测值进行两化改正[6]，接着计算附合单导线中往返测平距较差，往返测平距较差最大值统计结果见表4。

表4 附合单导线中往返测平距较差最大值

由表4可知，全站仪附合单导线中往返测平距较差满足相关规范要求。因此，实验网的GNSS以及全站仪附合单导线外业测量精度均达到设计精度要求。

3 测区垂线偏差值测定及其对进洞后视边水平方向观测值改正数的计算方法

地面上某一点的大地高和正常高的关系为

H=Hr+ε

(3)

式中，H为大地高；Hr为正常高；ε为高程异常。

当利用GNSS测定某一条基线时，根据式(3)，有

ΔH=ΔHr+Δε

(4)

式中，ΔH为基线两端点之间的大地高差，可由GNSS差分定位精确求得；ΔHr为基线两端点之间的正常高差，可由精密水准测量或精密三角高程测量确定；Δε为基线两端点间的高程异常差值，可由ΔH与ΔHr作差求得。

当基线AB两端点相距不远，且测区垂线偏差的变化大致可视为线性变化时，在求定基线两端点间的高程异常差值时[7]，有

(5)

式中，δA、δB为A、B两点的垂线偏差在AB方向上的分量。若设δA=δB=δ，有

(6)

式中，D为基线长，由GNSS相对定位得到[8]，有

δ=ξcosA+ηsinA

(7)

式中，A为AB方向的大地方位角；ζ、η分别为测区垂线偏差的子午分量和卯酉分量。若过某一个地面点有两条GNSS基线边，则有

(8)

解上述方程组可得

(9)

通过式(9)，可求出测区垂线偏差的子午分量ξ和卯酉分量η；同时，δ的精度会受到过同一点两基线之间的夹角(A1-A2)影响。理论上，当某一点出发的两基线间夹角为90°，求得的ζ、η值精度最佳。若受实际条件限制，夹角也不宜小于60°，否则，求得的垂线偏差精度较低。

昌都实验网进洞口处与出洞口处进洞联系测量后视点布设情况类似，故从进、出洞口处的进洞联系点与后视点形成的基线边中筛选出满足夹角要求的基线，利用最小二乘法(有多余观测的情况下)，即可求得进出洞口处的垂线偏差分量。实验网中满足夹角要求的基线部分相关观测值统计结果见表5。

表5中，基线长度及其两端点间的大地高高差值均通过高精度的GNSS相对定位得到，基线两点间正常高高差则是由精密三角高程测量得到。根据式(10)，加入上述基线边的大地方位角数据，可求出进出洞口处的垂线偏差分量。部分学者在使用GNSS法测定垂线偏差时，直接采用GNSS相对定位得到的基线边高斯坐标方位角代替基线边的大地方位角，但并未对GNSS法测定垂线偏差时使用基线边的高斯坐标方位角代替其大地方位角的可行性作出论证。为解决这一问题，以及求出正确的测区垂线偏差值及其对进洞后视边水平方向观测值的影响值，先利用高斯平均引数反算公式[7]求出上述基线的大地方位角(基线两端点的经纬度可由GNSS网三维无约束平差得到)，再分别使用上述基线的高斯坐标方位角和大地方位角，参与求解测区垂线偏差及其对进洞后视边水平方向观测值的影响值，若不同类型方位角参与求解得到的垂线偏差值及其影响值相差不大，则说明在使用GNSS法测定垂线偏差时，可以使用相关基线的高斯坐标方位角代替其大地方位角。

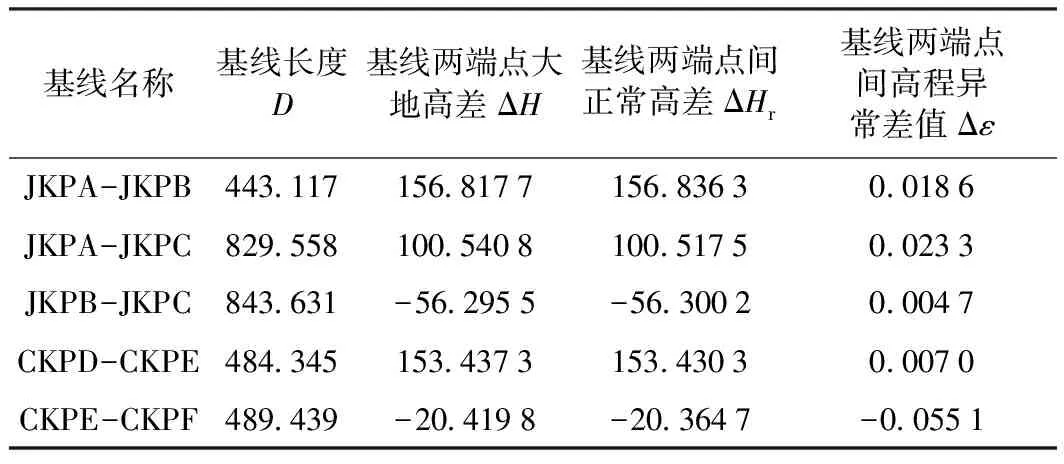
表5 进出洞口处基线的相关观测值 m

基线的高斯坐标方位角与大地方位角计算结果及其较差见表6。

表6 进、出洞口处基线边的高斯坐标方位角与大地方位角比较

采用不同类型方位角参与求解得到的测区垂线偏差分量计算结果见表7。

表7 测区垂线偏差分量计算结果

在求出测区垂线偏差分量值后，就可以对进洞后视边水平方向观测值按照式(1)进行垂线偏差改正。分别用进洞后视边的高斯坐标方位角与大地方位角参与解算，得到的垂线偏差改正数计算结果见表8。

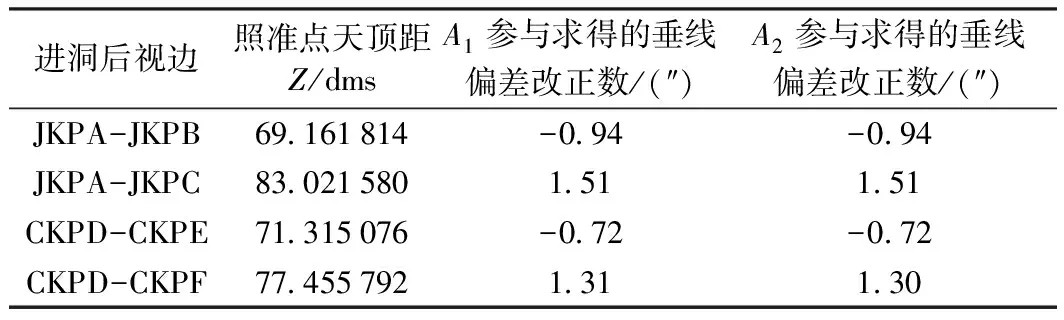
表8 进洞联系边垂线偏差改正数

由表6可知，相关基线的高斯坐标方位角与大地方位角差值的绝对值分布在108″±5″范围内，因此，同一测区基线边其高斯坐标方位角与大地方位角存在一定的系统性偏差。但结合表7、表8的结果可知，无论是相关基线的高斯坐标方位角还是大地方位角参与解算得到的垂线偏差及其对进洞后视边水平方向观测值的影响值，结果相差均不大。因此，在使用GNSS法测定垂线偏差时，可以使用相关基线的高斯坐标方位角代替其大地方位角参与解算。

4 不考虑垂线偏差影响的实验网精度情况

通过表8计算的结果可以看出，后视边JKPA-JKPC与CKPD-CKPF的水平方向观测值相较于其他进洞后视边受到垂线偏差的影响程度更大，为突出测区垂线偏差对进洞后视边水平方向观测值影响的程度，在后续计算中，仅将观测边JKPA-JKPC与CKPD-CKPF作为进洞联系测量的后视边。由于铁路隧道测量控制网一般采用工程独立坐标系，故对合格GNSS网外业观测的基线数据，可在工程独立坐标系下进行一点一方向平差，并将平差后得到的控制点JKPA、JKPC、CKPD与CKPF的坐标成果作为洞内附合单导线网的起算数据。

以下研究垂线偏差对长大隧道平面控制测量的影响情况，在相同的洞外GNSS网的起算数据下，对进洞后视边的水平方向观测值分别进行垂线偏差改正与不改正，并对比两种情况下得到的实验网的整网方位角闭合差及导线全长闭合差等指标进行统计；将实验网在模拟的贯通面处人为断开，并计算其横向贯通误差，以及将进洞方向和出洞方向到贯通点的支导线在贯通面两侧的观测边方位角(即支导线测量的方位角)与GNSS测量得到的方位角进行对比，旨在分析测区垂线偏差对模拟的洞内附合单导线控制网的影响程度。

4.1 洞内控制网方位角闭合差和导线全长相对闭合差计算结果

在不考虑垂线偏差对进洞后视边水平方向观测值影响的情况下，对全站仪测量的距离观测值进行两化改正和往返测平距取均值后[9]，加入起算数据，将计算得到的洞内附合单导线控制网的方位角闭合差和导线全长相对闭合差的结果统计见表9。

表9 不考虑垂线偏差影响时方位角闭合差和导线全长相对闭合差的统计值

4.2 横向贯通误差计算

长大隧道能够顺利贯通的前提取决于能否将贯通误差控制在合理的范围之内，而隧道的贯通误差又可以分解为纵向贯通误差、横向贯通误差和竖向贯通误差[10-13]，其中，横向贯通误差为沿垂直于隧道施工中线的水平方向贯通偏差，是制约长大铁路隧道能否顺利贯通的关键[14-15]。因此，通过对比横向贯通误差可以有效反映隧道洞内平面控制网的横向摆动程度。

根据《高速铁路工程测量规范》，在隧道贯通后，应在贯通面中线附近设1个临时点，由进出口两端的支导线分别测量该点的坐标，其坐标较差分别投影至线路中线及其垂直的方向上，即为纵向和横向贯通误差。因此，将实验网的附合单导线在模拟贯通点(即CP16控制点)处人为断开，在对进出口两端的支导线边长观测值进行两化改正后，分别计算贯通点的坐标和横向贯通误差。由于本次计算全部在工程独立坐标系内完成，坐标系纵坐标轴即为线路中线方向，坐标系横轴即为垂直于线路中线的方向，故由进出口两端的支导线分别计算得到的贯通点横坐标之差即为横向贯通误差。另外，分别将进出口两端的支导线计算得到的贯通面两侧观测边(即观测边CP15-CP16与CP16-CP17)方位角与GNSS网测量得到的方位角结果进行比较，结果见表10。

表10 不考虑垂线偏差影响时横向贯通误差计算和贯通面两侧观测边方位角比较结果

从表9、表10可以看出，在不考虑垂线偏差影响时，实验网的方位角闭合差、导线全长相对闭合差、横向贯通误差均能够满足规范的要求，且由进出口两端的支导线推算的贯通面两侧观测边的方位角与GNSS网的方位角也相差不大。

5 考虑垂线偏差影响时的实验网精度情况

首先利用表7中求得的测区垂线偏差值，对后视边JKPA-JKPC与CKPD-CKPF的水平方向值进行改正后，再分别进行计算。

5.1 附合路线方位角闭合差、导线全长相对闭合差计算

考虑垂线偏差影响后计算的洞内附合单导线控制网的方位角闭合差和导线全长相对闭合差结果统计见表11。

表11 方位角和导线全长相对闭合差的统计值

对比表11与表9可以发现，对进洞后视边水平方向观测值进行垂线偏差改正后，对于本次模拟的洞内附合单导线控制网而言，无论是方位角闭合差还是导线全长相对闭合差的精度均有一定提高，也说明测区垂线偏差会对隧道进洞后视边水平方向观测值产生一定程度的影响，这与上节中的定性分析结论一致。

5.2 横向贯通误差计算

考虑垂线偏差影响后，贯通点横向贯通误差和贯通面两侧观测边的方位角较差结果见表12。

对比表12与表10可以发现，对进洞后视边水平方向观测值进行垂线偏差改正后，计算得到的横向贯通误差减小28.94 mm，而贯通面两侧的观测边方位角与GNSS测量的方位角的较差值也分别减小-0.9″和1.82″。结合表11可知，对进洞后视边水平方向观测值进行垂线偏差改正，能够有效提高长大隧道洞内控制网的方位角精度，从而减小洞内平面控制网的横向摆动程度，使洞内横向贯通误差明显减小。

6 结论

通过进行垂线偏差对高原地区长大隧道平面控制测量影响的实验研究，得到以下主要结论。

(1)测区的垂线偏差主要影响进洞后视边两端高差较大时的水平方向观测值，对隧道洞内平面控制网观测边水平方向观测值的影响较小。

(2)利用GNSS法测定测区垂线偏差值时，选取不同的基线会影响求解的垂线偏差值的精度，应尽量选取夹角为60°～90°基线观测值参与垂线偏差值的计算。

(3)对高原地区的长大隧道洞内平面控制网的进洞后视边水平方向观测值进行垂线偏差改正后，能够在一定程度上提高洞内平面控制网的方位角闭合差以及导线全长相对闭合差等精度指标，并减小横向贯通误差值。

(4)在使用GNSS法测定测区垂线偏差和计算其对水平方向的影响值时，可以使用相关基线的高斯坐标方位角代替其大地方位角参与解算。