倒伞型曝气头气液两相流场数值模拟研究

胡钰贤,贾冬冬,郭亚兵,陈兵

(1.太原科技大学 环境与安全学院，太原 030024; 2.北方自动控制技术研究所，太原 030009)

0 引言

倒伞型曝气头是广泛应用于氧化沟污、废水处理工艺中的一种表面曝气设备，具有良好的充氧、推流等作用。主要由电机、调速装置和倒伞叶轮三个部分构成。倒伞型曝气头是由电机驱动高速旋转，曝气池中流体在叶轮的旋转推进作用下拥有离心力，从叶轮边缘部分甩出，形成径向流并与空气接触，从而带进大量空气以实现曝气的效果的表面曝气设备。倒伞型曝气头具备对氧化沟内部充氧、搅拌和推流的作用。

倒伞型曝气头的开发与应用最早是由国外公司提出，比较出名的公司有荷兰DHV公司和Spaans Babcock bv公司、美国EIMCO公司等。荷兰的Spaans Babcock bv公司自1970年生产Spaans-A型倒伞型曝气头，该曝气头由一个倒置的圆锥和8个叶片组成；后在此基础上进行升级改造为Spaans-B型倒伞型曝气头。美国EIMCO公司主要生产Oxyrator型倒伞型曝气头。国内倒伞型曝气头的发展时间虽较晚，目前业已研发出一些新型的倒伞型曝气头，如上海市政工程设计院设计的国产化的Simcor倒伞型曝气头和安徽国祯环保公司研发的1DS立式倒伞型曝气头等。倒伞曝气头在我国水厂广为使用。但大多倒伞曝气头设备体积较大，很难找出理想场地进行试验，设备结构优化困难。通过ANSYS CFX仿真软件对设备性能进行模拟，分析反应器内部流场的特征，通过改变倒伞型型曝气叶轮的工况，得出最佳运行工况及设备参数；同时，数学模拟可以较为深刻的探究设备结构的曝气性能的影响机理，为实验及设备优化提供指导。

目前，国内外多位许多研究者应用仿真模拟软件模拟流场，研究分析倒伞型曝气头驱动流场的水力学特征。1997年侯拴弟研究了搅拌槽内三维流场实验及数值模拟[1]。2004年AUBIN等[2]使用PIV(粒子图像测速)测量了上下轴流式叶轮搅拌的充气罐中的流量。2005年,LAAKKONEN等[3]研究了搅拌容器中气液界面区域气泡的分布。2008年,MONTANTE等[4]研究了搅拌槽内的气液流量和气泡尺寸分布。2009年,许丹宇[5]采用CFD数值计算的方法研究了卡鲁塞尔氧化沟工艺的污水—污泥两相水力特性。2012年ACHOURI等[6]应用三维CFD模型模拟研究了倾斜叶轮对流场的影响。2013年LAU等[7]研究了密集气泡流中气泡尺寸分布。2016年邓志雄[8]就新型倒伞型表面曝气机推流充氧机理及试验进行了研究，利用有限元分析确定了一种曲面形状受非等角对数螺旋线曲面约束的新型曝气头叶片。2017年MURGAN等[9]使用PIV和LIF(荧光粒子)研究了气泡柱流的特征。以上研究，多是对容器罐中单一搅拌装置对罐内气液两相流流场的初步模拟研究，但对不同结构曝气头驱动流场的变化问题及曝气头压强分布情况没有作深入对比研究。

本研究通过模拟分析氧化沟中两种不同结构的倒伞型曝气头附近流场中气液两相流场流动特性和叶轮背面压强分布情况，探索复杂边界条件下反应器内流场的模拟方法，为倒伞型曝气头的优化研发提供理论依据。

1 CFD模型

1.1 物理模型创建

依据几何相似原则使用CFX前处理器的建模工具进行建模，如图1所示为此次研究模拟所建小试模型Landy7(a)与Hubert(b)。Landy7与Hubert的结构主要分别由7个和8个径向分布均匀的直立叶片构成，伞体直径相等为0.3 m，其中Landy7伞体为封闭式的大叶片式倒伞型结构和Hubert伞体呈开口式的倒置圆锥体。

(a)Landy7

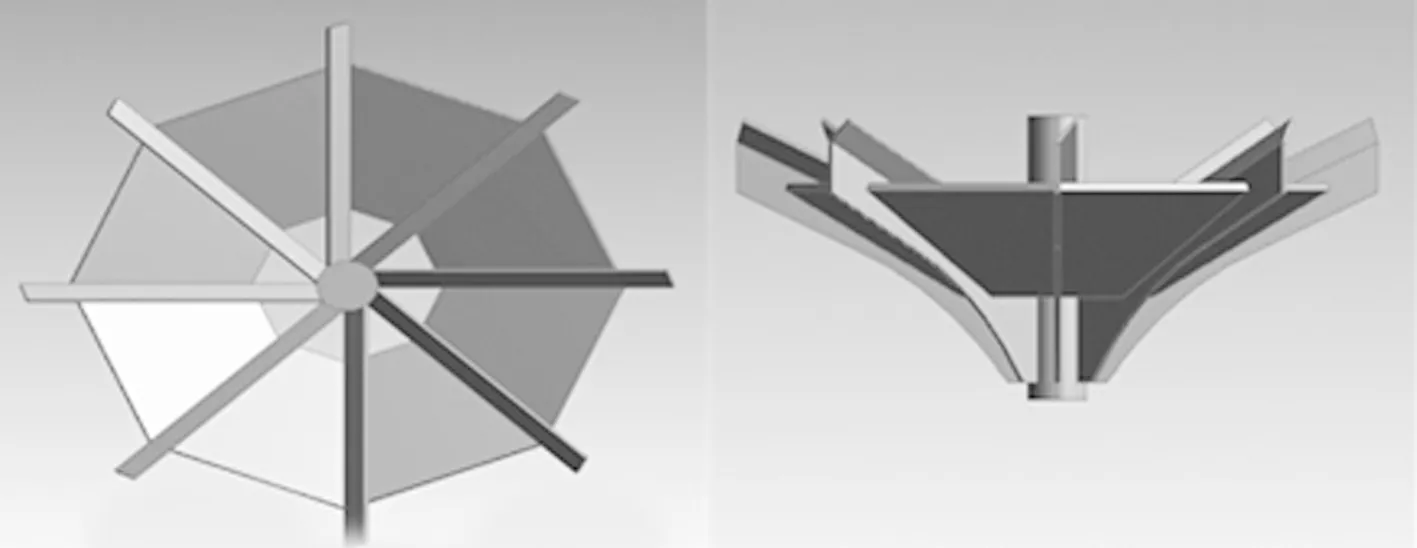
(b)Hubert

所建叶轮模型相对位置在一个高为1.2 m，长和宽均为1 m的一个顶部开口的矩形曝气池中，且叶轮均固定于池体中心位置，即叶轮几何中心所在平面距池体距离为0.6m，且在几何中心处建立三维坐标系，z轴垂直于纸面向里为正，如图2所示。

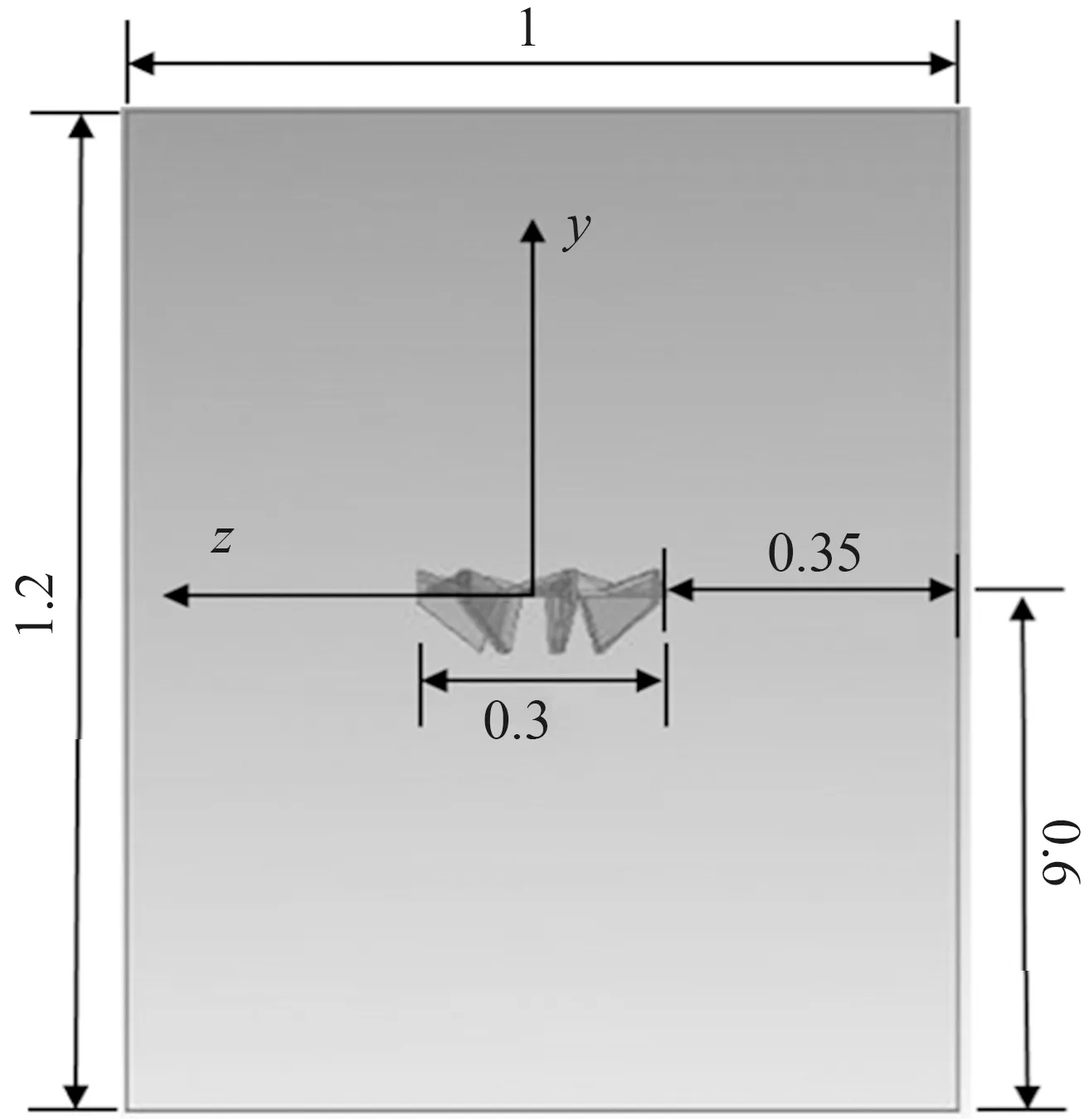
(a)Landy7 单位：m

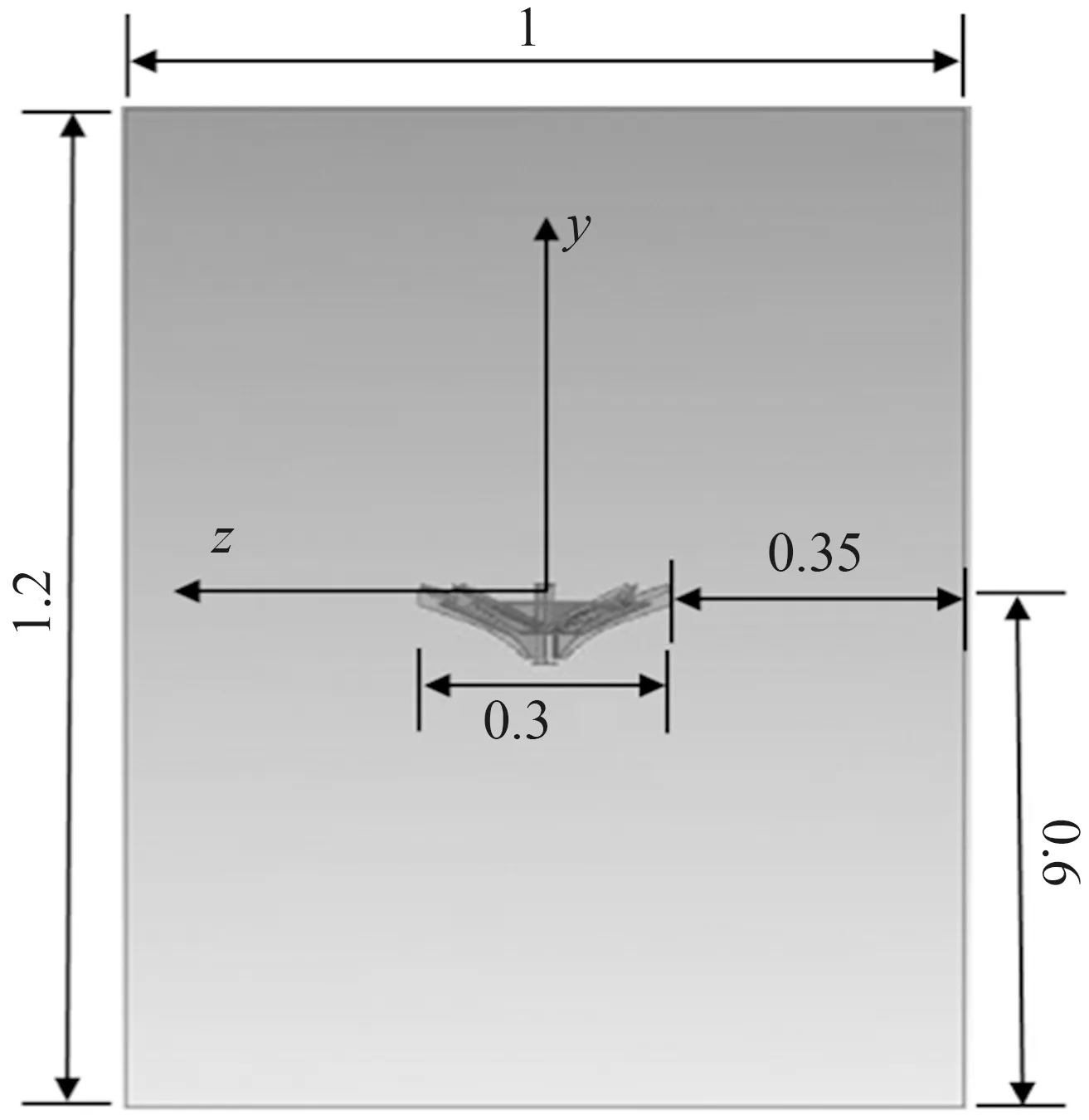
(b)Hubert

1.2 网格划分

在CFX软件中采用网格划分模块Meshing将建好的模型分别进行网格划分。针对研究的模型结构，网格划分采用自动网格划分方法，相较于以四面体或六面体为主导的网格来说，该方法划分的网格能够更好的适用于本研究的模型[10]。网格数量越多及质量越高(网格质量一般要求0.7～1，数值越高质量越高[11])，则模拟计算结果越精确，但数量越多耗费时间越长，同时对计算机性能要求也越高。如图3所示为曝气池区域及叶轮网格划分示意图，网格数量及质量满足此次模拟计算的要求。网格数及质量见表1。

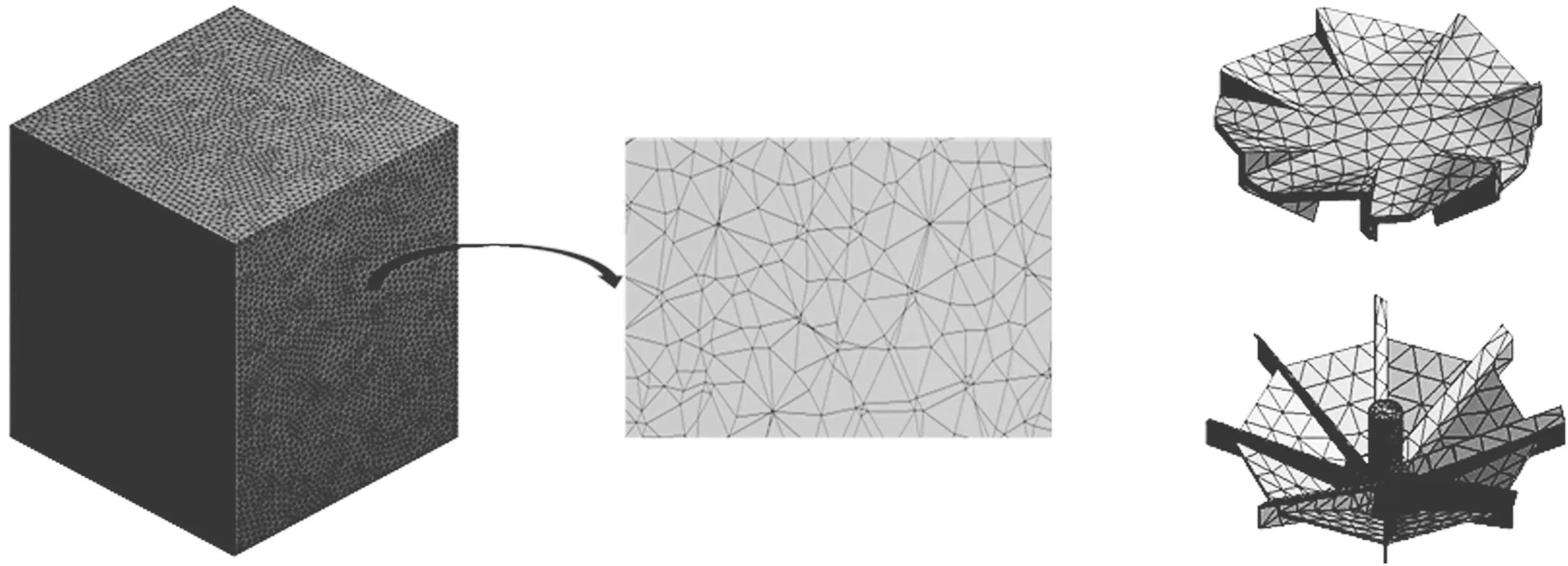
图3 曝气池区域及叶轮网格划分

表1 两种结构模型的网格数量及质量

1.3 CFD模型方程

ANSYS CFX中提供了Eulerian-Eulerian(连续两相流模型)和Lagrangian Particle Tracking(离散相模型)两种多相流模型。依据研究模拟的问题，此次模拟计算将气、液两相视为连续两相流问题，因此选择的是Eulerian-Eulerian多相流模型中的自由表面模型(free surface model)，该模型属于非均匀模型，且此次模拟不考虑气液两相间的质量传递。动量的界面传递依赖气液两相之间的接触面积，可用两相α与β间单位体积的接触面积Aαβ来表示:

Aαβ=|rα|。

(1)

流体的流动均遵循守恒定律，其守恒方程如下：

连续性方程：

(2)

式中：SMSα定义的质量源项。

体积守恒方程：

(3)

动量方程：

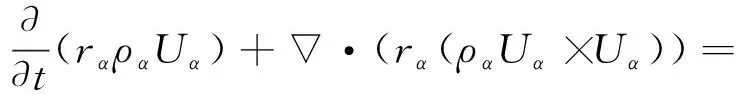
-rαpα+·(rαμα(Uα+(Uα)T))+Mα+SMα,

(4)

式中：Mα为其他相作用在相α上的力；SMα为由外部质量力引起的动量源项和定义的动量源项。

模拟过程中，流场属于完全湍流的流动且曝气头驱动流场的水力学现象比较复杂，为了减少计算时间和保持计算精度，因此，模拟计算所选取的湍流模型为标准k-ε模型。

标准k-ε模型的输运方程可表示为：

(5)

式中：Gk是k的产生项；Gb由浮力引起的生成项，此次模拟为不可压缩流体，Gb和YM均为0。

在标准k-ε模型中，Cη=0.09，σε=1.3，σk=1.0,C1ε=1.44,C2ε=1.92。

1.4 边界条件

维持两种结构叶轮所处运行环境相同，对两个曝气装置分别创建流体域(水和25 ℃空气)和浸没实体域(叶轮)，考虑到两种结构小试模型叶轮的临界旋转速度后，在叶轮周围的移动区域使用“移动参考系”边界条件，转速设为n=140 r/min；叶轮浸没深度为0.07 m，即叶轮几何中心所在平面距水体表面的距离；选择计算模拟的流体分析类型为非稳态，将模拟流场分为静止区域、叶轮区域以及叶轮旋转驱动流体的流动区域；由于大气压力位于叶轮顶部，因此设置空气入口的边界条件为“静压入口”状态，以及曝气池顶部的“压力出口”边界条件，但不设置入口处的流体流速；同时设置无滑移的壁面边界条件。通过BN等[12]的研究工作表明,此次对模型和边界条件的选择是可行的。

2 结果分析

叶轮的曝气效果是判断其性能的主要指标。Landy7和水体积分数等于1的等值面轮廓见图4，从图4可见，保持叶轮转速恒定(n=140 r/min)，曝气池中气液界面随时间的变化情况，可由水的体积分数等于1的等值面来表示。观察可知，等值面逐渐扩散到池体底部，因此确保了流体的完全混合与自由表面存在气体。

(a)Landy7

(b)Hubert

2.1 压力分析

由于叶轮的高速旋转，叶片背侧形成负压区，曝气时气体被吸入该区域形成气腔，通过叶片周围的涡流将空气截切并细化，并进行搅拌掺混。因此，在对曝气头的性能进行讨论时，可通过分析叶轮上下产生的压差来判断曝气效果。由于作用在叶轮上的大气压值不变，其负压值越小，则所产生的压差就越大，有助于更多的空气与液体混合达到更佳的曝气性能。此次模拟的两种不同结构曝气头所处环境相同，作用在上面的大气压值相等，可以分别通过分析两种结构叶轮驱动流场所产生的压差来判断其性能。图5所示为两种结构叶轮背侧压强分布情况，由图5可知，形成的负压区主要集中在叶片附近区域，且Landy7与Hubert叶轮背侧形成的最大负压分别为3 132.735 Pa和16 179.507 Pa。观察两种结构叶轮背侧整体区域的压强变化得出Landy7叶轮背侧形成的压差较大，由此可知该结构的叶轮在曝气池中曝气性能较佳。

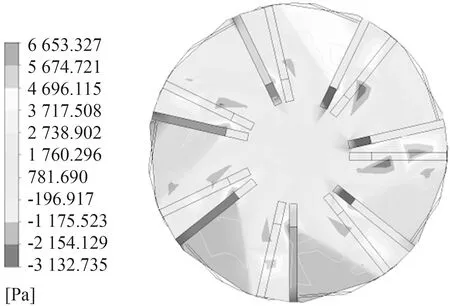
(a)Landy7

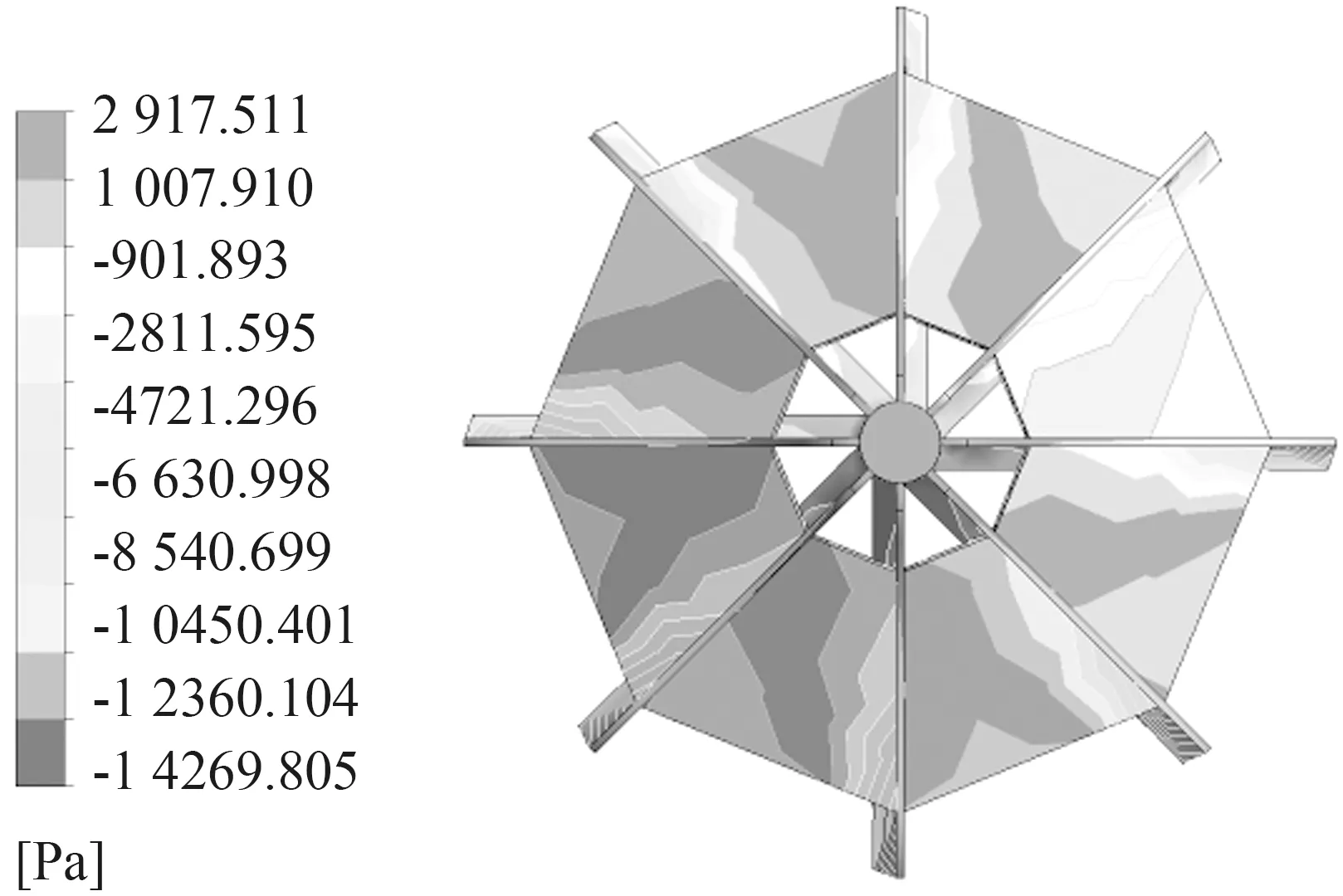
(b)Hubert

2.2 液相流场

对比两种不同结构曝气头驱动池内流场的液相速度变化情况，结果如图6～图10所示。由图6所示，在某一时间点过叶轮轴心截面(z=0)上，形成了伴有涡流存在的左、右双循环的流场结构。

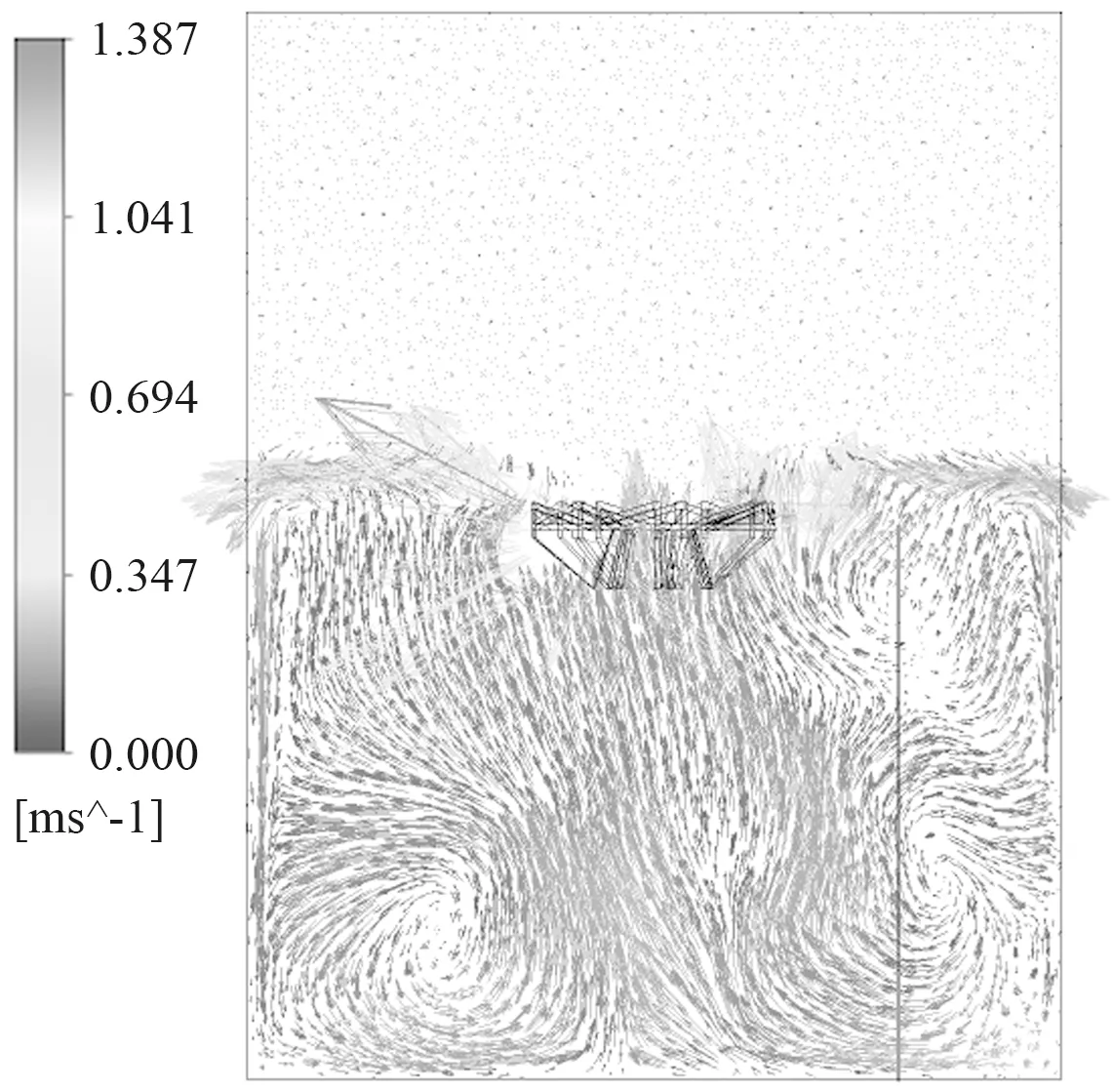
(a)Landy7

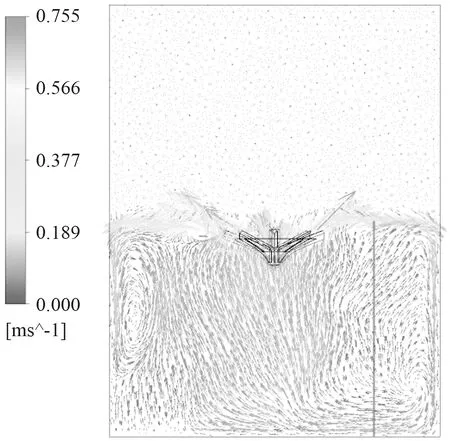
(b)Hubert

分析两种结构曝气头对池体底部水体的推流状态，在图6所示图(a)与(b)中各取一条x=-0.3 m的直线line1和line2，并观察液相在线上的速度分布情况，结果如图7所示。观察图中直线上的速度分布，其中由于line2大多位于同一涡流内，速度整体呈现出较为平稳的趋势，且在靠近池底部分速度逐渐减小为0.008 m/s左右；涡流的复杂程度能够体现出流场结构的复杂性，对比图6中两个液相速度矢量图，图(a)中产生的涡流较为复杂，因此，Landy7的液相流场结构复杂。在line1上有两个明显的同向逆时针方向的涡流存在，line1速度变化相对较大，液流动能较强，Landy7的大叶片式倒伞型结构高速运动在叶片背侧形成较大负压区是此流场变化的主要原因。

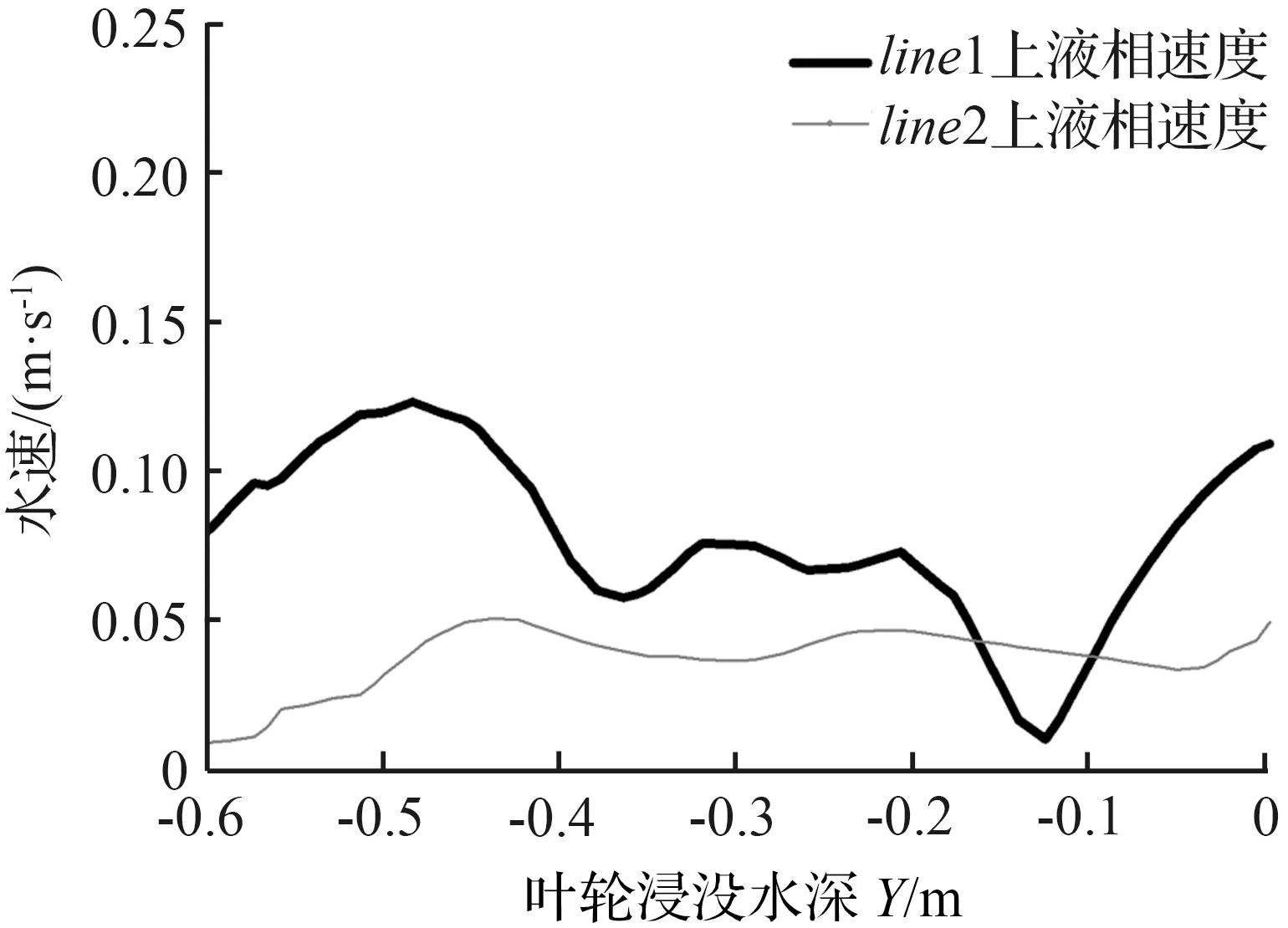
图7 Line1与line2水速度分布

同时叶轮旋转时对液体表面的搅拌能力也能体现出其性能，图8所示为Landy7与Hubert叶轮旋转时驱动水体自由表面上的速度分布情况，最大速度分别可达0.623 m/s和0.192 m/s，依据动量守恒定律，表面所产生的动能将随着流动的水体逐步传递到下层水域中。观察整个水体自由表面上的速度分布情况可知Landy7对其表面的搅拌能力较强，增加了下层水域水体的平均流速，图9所示为y=-0.5 m处的平面水体速度分布情况，由图9可知，对比两种结构叶轮，Landy7对该平面上水体的整体搅拌速度较大为0.254 m/s。因而该结构叶轮较Hubert对曝气池底部水体的推流能力更强。

(a)Landy7

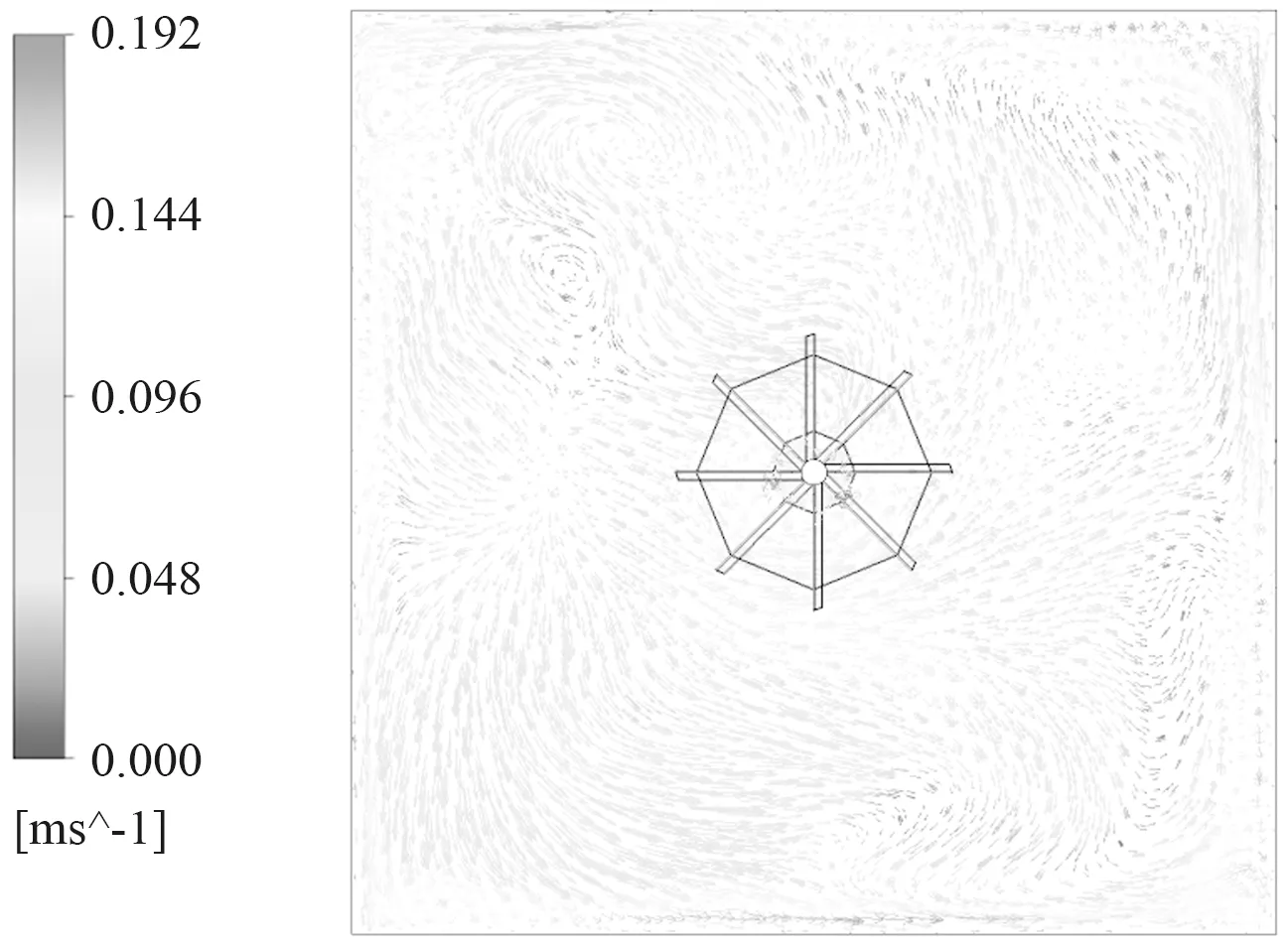
(b)Hubert

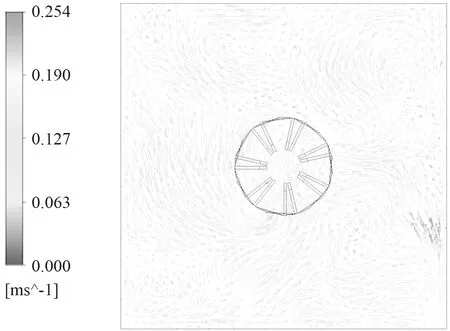
(a)Landy7

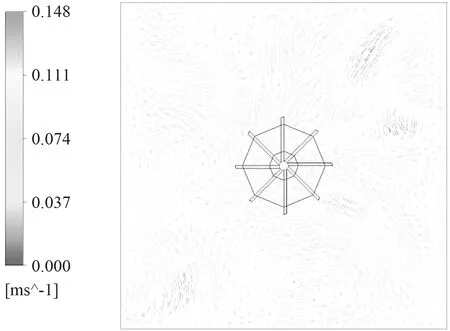
(b)Hubert

图10所示为叶轮下部中心区域(x=0 m，z=0 m)液相速度分布情况处，由图可知，在靠近Landy7与Hubert叶轮中心区域水体速度较大，分别达到0.24 m/s和0.13 m/s左右，随着深度的增加在靠近池底时水体整体流速分别逐渐减小为0.080 m/s和0.065 m/s左右，同时可得出Landy7叶轮推流水体的性能较后者高。注意到Hubert水流速度下降趋势较平缓，而Landy7水流速度呈现出先降后升的趋势，由图6(a)和图7分析可知，是由于在y=-0.35～-0.10 m部分区域存在的涡流造成的影响。Landy7底部涡流存在，充分搅动了氧化沟底部流场，对氧化沟底部流场推动作用优于Hubert曝气头。

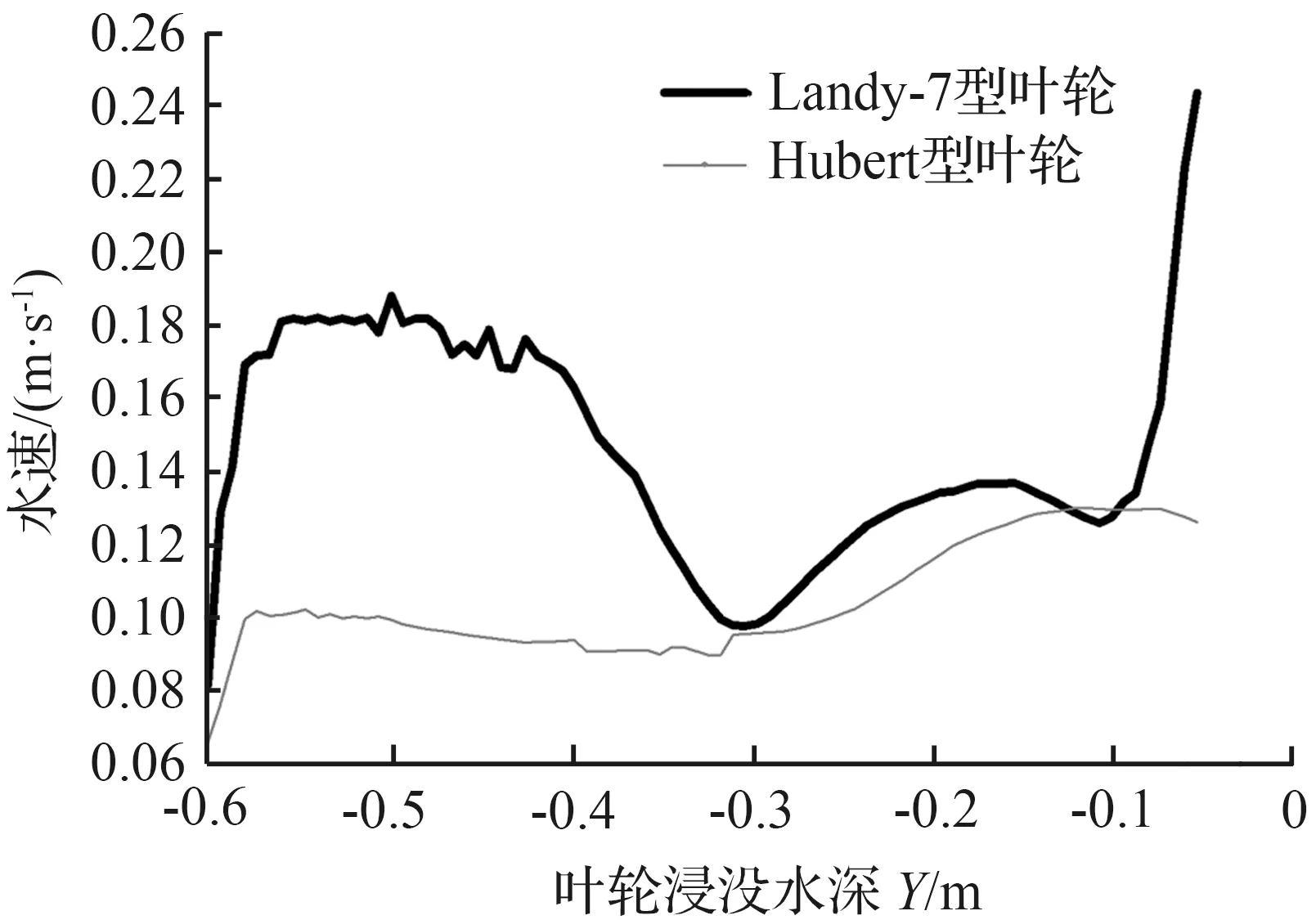
图10 叶轮下部中心区域速度分布(x=0 m，z=0 m)

3 结论

通过对以上两种结构叶轮的分析，可以得出叶轮转速n=140 r/min时，Landy7叶轮所形成的压差与Hubert相比较大，且Landy7叶轮对曝气池中自由液面的搅动效果较大，最大速度达到0.623 m/s；同时Landy7叶轮对曝气池底层的推流搅拌性能强于Hubert。综合分析对比，大叶片式倒伞型结构Landy7表曝机无论是在曝气方面，还是在推流搅拌能力方面都表现出了良好的性能。

曝气池及表面曝气头的运行过程较为复杂，此次研究模拟是按一定比例缩小的模型下进行的，虽有一定的局限性，但模拟结果具有较高的精确性，且不会影响曝气头驱动流场的大致趋势。