Unity3D机器人焊接焊缝自动提取及轨迹规划与仿真*

陈子健，卓 勇，唐炳洋

(厦门大学 航空航天学院，福建 厦门 361102)

0 引言

虚拟现实[1](Virtual Reality，简称VR)已经在各领域得到应用,被认为是影响人类生活的重要技术之一。随着国家和市场对工业机器人的需求不断增长，各大高校也在开设机器人相关课程与实训，但机器人价格昂贵、数量少，不能满足教学需求，焊接作业环境经常是复杂、恶劣的，用真实机器人对作业人员进行培训的成本高、危险性大[2]。因此，使用VR可有效规避风险、满足要求。国外机器人相对成熟，也开发了相应的仿真软件[3]，但一般都是针对自己公司的产品，进行购买也会扩大投入，不一定适合所有学校或企业。

Unity3D(下文简称Unity)是一款优秀的跨多平台的虚拟引擎[4]。目前部分学者在此虚拟环境中进行机器人虚拟仿真并取得一定成果。例如，高国雪等[5]搭建虚拟仿真环境实现同步运动；刘俊等[6]将Unity仿真环境应用在机器人仿真上满足教学需求；刘谋玉等[7]运用Unity虚拟环境实现机器人遥操作系统；岑洎涛等[8]基于Unity平台搭建一个跨平台的机器人仿真系统；刘宇轩等[9]基于Unity搭建一个人机交互的教学平台。这些系统的搭建基本都是基于人工示教或作为教学展示加强对机器人的理解。机器人编程方式常用的有离线和再现示教两种。示教编程简单易学、精度低、操作繁琐、不安全；离线编程高效，但对使用者要求较高，并且没有统一通用的离线编程软件[6]。综上所述，为了尽可能的利用各自优势，本文利用VR的强交互能力，将简单离线编程与其结合，实现焊件焊缝自动提取，并实现工业机器人自动进行焊接仿真的轨迹规划过程。

对上述其他作者搭建的系统进行研究，发现基本都是基于人工示教或作为教学展示加强对机器人的理解。本文通过特征提取算法实现自动提取特征线，通过直接选择焊缝实现自动焊接仿真加工过程，从而避免一个个选取点进行人工示教，也避免了示教精度不足的问题。仿真确认无误后，可以输出机器人语言程序，用于实际的生产或教学当中。

1 系统平台框架搭建

VR系统要求对实体与环境的模拟实时逼真，仿照真实场景建立如图1所示的系统平台。本文选用SolidWorks软件进行高效建模和3ds Max进行渲染，获得与Unity兼容的FBX格式的模型文件[10]，结合二者优势进行系统平台的搭建[11]。本文机器人焊接虚拟仿真系统主要由焊接过程所需的机械、电气及焊接装置三部分组成。包括安全围栏、变位机、公共基座、操作台、机器人本体、固定工作台、夹具、电缆桥架以及机器人控制器和焊机等部分[12]。

图1 系统总体框架结构图

本系统使用Unity内置的UI组件设计功能面板，用于实现人机交互的功能，方便作业人员快速寻找自己想要实现的功能。最终在Unity中布置好场景后，可以看到如图2所示的整体布局界面。

图2 UI面板和仿真场景

2 特征提取

本文通过获取焊接模型的三角网格顶点信息，并经过重复点剔除、重组后建立新的拓扑关系，然后根据特征点的识别条件提取模型中的特征点并存入集合进行存储管理，最后按照给定的规则将特征点连接成特征线并显示出来。总体思路如图3所示。

图3 特征提取总体思路

2.1 三角网格模型拓扑信息重建

Unity中的模型均为三角网格结构，缺乏实体信息。Unity提供Mesh类，用于存储网格信息且可再次编辑。Unity中的网格模型包含了大量散乱、无序的三角面片，造成大量的顶点冗余现象。因此需要剔除大量冗余点，并重建三角面片的拓扑关系。根据Unity中网格模型的特点以及三角面片规则，本文利用基于排序的三角网格模型快速拓扑重建算法。

(1)冗余点剔除

本文建立Vertex类，用于模型中顶点信息的存储及处理。重写Vertex类中继承自IEquatable接口的Equals()比较函数，以两顶点坐标值大小作为判断顶点是否相同的标准。

重复点剔除的关键是保证数据的唯一性。本文利用C#中的HashSet集合进行重复点的剔除，再对顶点进行重新编号，对于HashSet中每个数据都对应一个唯一的键值，保证了数据的唯一性。

(2)三角面片顶点序号更新

随着顶点的去重，需要对三角面片中的顶点序号进行更新。建立Triangle类用于三角面片数据的存储与处理。通过id进行顶点的索引，减少内存占用。

使用Dictionary字典集合容器对三角面片中的顶点进行检索，与剔除重复点后的顶点新集合进行比较，更新三角面片的顶点序号。

(3)三角面片邻接信息的获取

对于满足充满原则[13]的网格模型，每条边均被两个三角形共用，因此每个三角形有三个邻接三角形，据此特点可以找到三角面片的所有邻接三角形。

2.2 三角网格模型特征提取

为了准确完整地提取模型的特征边，本文的特征边提取算法主要分为两步：首先通过模型边的二面角进行特征边的初步提取，再通过顶点的曲率判断，获取遗漏的特征点，并利用点与边的几何依存关系，获取遗漏的特征边。

2.2.1 基于二面角的特征提取

本文首先对网格模型中所有的三角形边求解基于两个相邻三角形的二面角，再按照一定的规则设定阈值，若大于设定阈值，则该边为特征边，特征边线上的两个顶点为特征点。

(1)三角形边的二面角求解

构建Segment类，用于边信息的存储与编辑处理。由空间几何关系，通过两个邻接三角形的单位外法线，可以求得边的二面角。

(1)

式中，n1,n2为邻接三角形的单位外法线。

(2)通过阈值筛选特征点

通过分析其他的基本几何体可知，只需剔除其光滑表面上的边，剩下的边即为特征边，阈值可以通过其上界和下界进行确定[14]。一般地，根据基本几何体模型的统计规律及工程经验，其无特征边的光滑曲面上二面角不大于20°，因此可以遍历模型所有的二面角得到小于20°的最大角度值β，作为确定阈值α的下界；同时以大于20°的最小角度值γ作为确定阈值α的上界，则可得：

(2)

因此，例如在立方体模型中，β值取0°，γ值取90°，阈值α可以选择45°。

对于本文系统焊接模块讨论的几何体由基本几何体组成，因此特征边可以通过式进行筛选得到，但由于复杂几何体三角形的形状不一，仅通过单一的阈值难以提取到完整的边界特征。例如图4中由尖锐的狭长三角形连接得到的边，其二面角小于阈值，却是特征边线。

(a) 模型中的边 (b) 狭长三角形示意图 图4 狭长三角形构成的边

一般情况都是通过公共边上高的比值进行判断是否是狭长的三角形，但仅通过三点坐标进行高的求解较为复杂，效率低。本文改进后，通过另外两条边长之和的比值进行判断。记两个三角形中除公共边外的边长之和的比值为τ，则其表达式为：

(3)

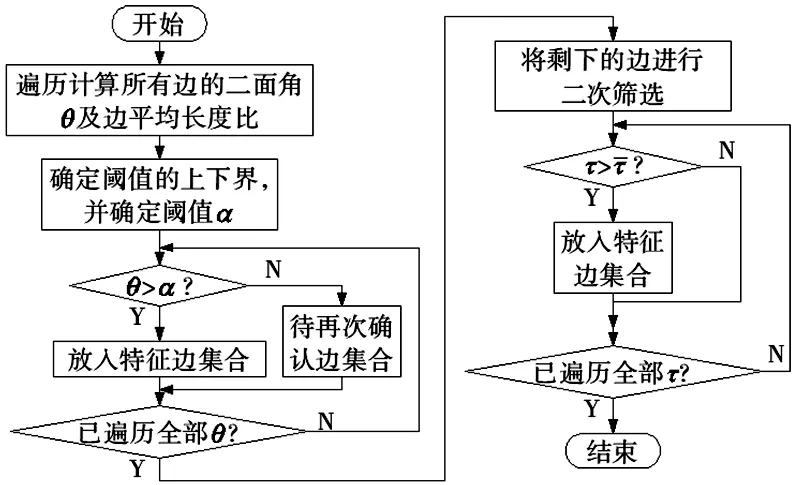
图5 基于二面角的特征提取算法流程

2.2.2 基于曲率判断的特征提取

首先通过各顶点的法矢量构建二次曲面，并计算该曲面在各顶点上的曲率半径，然后经过相应的判断获取特征点，并由顶点与边的几何依存关系，遍历寻找到组成模型的三角面片的边，即特征边。

(1)顶点法向量的获取

顶点法向量是曲率计算的基础，Unity中Mesh包含了顶点的法向量信息，可以直接获取。

(2)顶点曲率的计算

本文主要使用曲面局部拟合法[15]的思想，首先任取一个顶点，将该点与所有的邻接点构建二次曲面，由此得到该点处的主曲率与其方向。

对于顶点P，存在邻接点Vi,i=1,2...n，如图6所示在P点处建立局部坐标系Puvw，其邻接点转换到Puvw内的坐标为(ui,vi,wi)，二次曲面拟合顶点P及其邻接点

S(u,v)=(u,v,w(u,v))

(4)

其中，w(u,v)=au2+buv+cv2由式(4)可以得到线性方程组(5)：

(5)

上述方程可以通过最小二乘法进行二次曲面系数a、b、c的求解。这种解适合均匀的三角网格模型，但在本文中2.2.1节中已经剔除了狭长三角形的情况，因此可以认为是均匀化的情况。

(3)特征点的判别

遍历模型中除去2.2.1小节已经筛选出来的顶点，通过对点的主曲率极值的判断，通过判断不同方向上曲率极值点来进一步筛选特征点，若如图6所示两个方向上均为极值点，则该点为特征点。具体筛选方法见参考文献[15]。

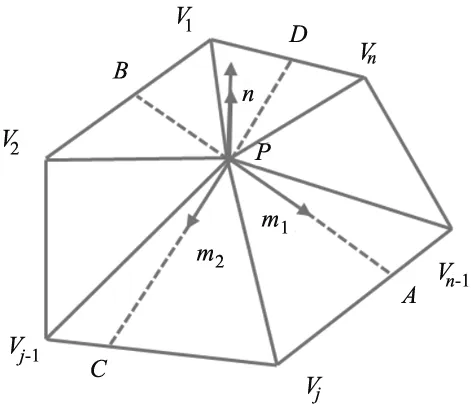
图6 主曲率的极值点

(4)误差消除

由于曲率的计算是不准确的，根据上述方法得到的特征点的数量大于实际所需的，本文根据参考文献[15]中的方法，加入误差消除因子与整体误差消除因子，进行误差点的剔除。

2.3 特征边自动生长算法

前文通过特征提取算法得到的网格模型特征仅是离散的特征边(实际获得的为特征点，由顶点与边的依存关系，可以寻找到三角面片的边)，相互之间没有顺序关系，难以直接用于机器人的轨迹规划，因此需要对得到的特征边进行排序。本文利用基于顶点邻接数的特征边自动生长算法[15]，能够将离散的特征边进行整合排序，快速得到完整的模型边界。

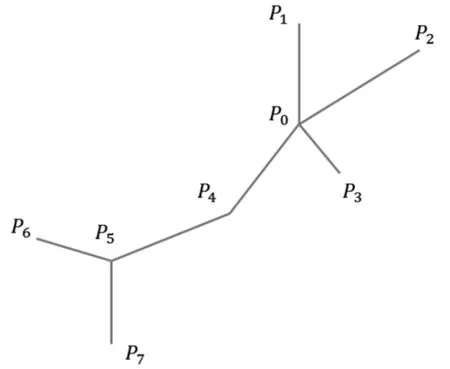
图7 特征线自动生长

算法根据模型边界是否闭合，将其分为特征链与特征环两类。两者排序算法基本一致，只是算法的终止条件略有不同。获取所有邻接点大于2的特征边顶点，即存在开叉现象的特征点。如图7所示的P0、P5点是个开叉点，这类点一般作为特征链的起止点。例如P0可以出现在4条特征链中，设置可使用次数为4；P4仅具有2个邻接点，这类点则作为特征链的中间点，仅会出现在一条特征链中，可使用次数为1。步骤如图8所示。

图8 获取完整特征线流程框图

特征环的终止条件为：终止点与起始点相同，其他的步骤与特征链相似，不再赘述。

3 三次样条插值

当外部输入的模型精度不高时，直接获取到的边界线精度较低，因此需进一步处理，提高其精度满足机器人运动仿真的需求。对于直线可以直接使用直线插值获取仿真点，曲线选用三次样条曲线插值。本文使用基于累加弦长的三次参数样条曲线插值算法进行曲线的二次拟合与插值。

设第i段三次参数样条曲线的表达式为：

Pi(t)=B1+B2t+B3t2+B4t3,t∈[0,Li]

(6)

式中，Li为第i段的弦长。

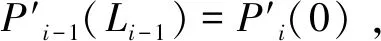
(7)

使用对角矩阵追赶法对上式进行求解可以得到二阶导Mi的值，可求得第i段的三次样条曲线表达式。本文系统中建立Spine类进行三次样条曲线插值处理，应用三次样条插值算法后得到的圆柱边界如图9所示，结果表明，特征线的精度提升明显。

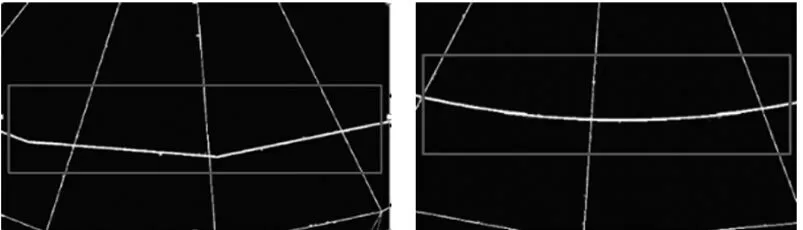
(a) 未插值处理的圆弧 (b) 插值处理的圆弧 图9 圆弧插值处理前后

4 机器人逆解和焊接仿真

为了实现用户点击特征线后，机器人自动进行自动焊接运动，无需人工示教，需通过机器人逆运动学求解出机器人6个关节角度值[17]，并反馈给机器人使其运动。利用贪婪算法其局部最优解的思想，将所有解与上一状态进行对比，差值最小解即为需要的最优解。具体求解方法请见参考文献[17]。本文在Unity中选用C#语言进行程序的编写，使用Transform组件中的局部旋转的成员变量可以实现各个关节的相对旋转，同时根据焊缝的位置来自动改变焊枪位姿，尽可能保持垂直焊接，从而实现焊缝自动焊接的轨迹规划过程。

4.1 机器人仿真结果展示

本文基于Unity 5.6.0版本，使用C#脚本在Visual Studio 2015外部编辑器进行代码编写、编译、测试，同时，可以在面板上点击模型选择的按钮，根据需要选择如图10a所示不同类型的焊接模型，便可更改图10b中焊接对象的仿真模型并在场景中显示更新的模型。点击UI界面上的特征提取按钮后可看到生成的特征线(图中黑色线框)。通过选取焊缝，同时可显示出如图11所示准备进行运动仿真的预定轨迹。通过控制面板的开始按钮让机器人运动，仿真过程如图12所示。操作者可以随时通过鼠标改变视角观察任何部位，或暂停观察。在界面右下角设置一个小窗口用于跟踪放大焊接详情，便于观察焊枪所走路径是否正确。本文对于直线和曲线进行算法测试，均可以取得良好的视觉效果，将特征提取获取的特征点与三维软件中获取的特征点进行对比，效果如图13所示，从图中可以看出，两者基本可以实现重合。将两者数据进行拟合对比，以多项式函数作为对比标准，发现两者相关系数R2分别为0.9243和0.9236，差值低于0.001，说明本文提取到的特征线基本可以满足普通的加工或者教学要求。

(a) 模型选择面板 (b) 相应模型显示 图10 模型选择及显示

(a) 直线仿真轨迹 (b) 曲线仿真轨迹 图11 仿真轨迹展示

图12 仿真运动及路径观察窗口

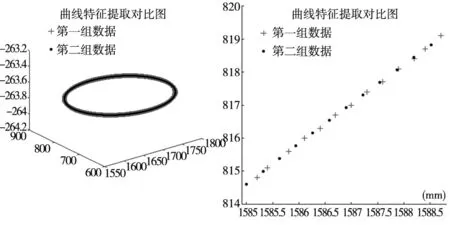
(a) 曲线特征点 (b) 特征点放大对比 图13 仿真点数据验证

5 结束语

本文选用Unity进行虚拟仿真研究，从外部软件导入模型搭建了一个6关节机器人焊接的虚拟仿真系统。通过对三角网格模型进行基本信息的提取、重组，采用特征提取算法获取特征点，连接得到完整的边界曲线，最后进行三次样条曲线的拟合得到运动轨迹进行焊接仿真。确认无误后，可以输出机器人语言程序，用于实际的生产或教学当中。这种方式具有良好的临场感和交互性，同时带给操作者良好的视觉冲击，有效逼真的代替真实机器人进行加工训练和教学，降低作业风险、培训成本和环境污染。本文对于仿真过程自动躲避障碍物还有所不足，以后可以结合机器视觉、图像处理等技术进一步识别障碍物并自动实现躲避，重新规划仿真路径。