超精密机床系统动力学参数辨识研究*

商兴莲，王国平，芮筱亭，陈刚利

(南京理工大学 发射动力学研究所，南京 210094)

0 引言

超精密加工技术是关乎国家安全和尖端科技的重要技术，是现代高技术战争的重要支撑，也是现代基础科学技术发展的重要保障，在航空航天、精密仪器、军事工业等诸多领域发挥着越来越重要的作用[1-2]。超精密机床作为超精密加工的重要载体，直接决定了零件加工的精度、可靠性和稳定性，因此加强对超精密机床的研制是提高我国超精密加工技术的重要途径。

超精密机床结构复杂，加工精度要求高，因此对其进行动力学建模、动力学参数辨识、动态性能等问题研究时会面临系统总体动力学方程建立过程繁琐，计算工作量大，计算“病态”等诸多问题。而准确建立超精密机床系统的动力学模型并准确辨识其动力学参数是动力学分析的关键，将为超精密机床系统的设计与优化提供重要依据。多年来，海内外专家学者不断提出和发展了多种参数辨识方法，如最小二乘辨识、小波变换、状态空间实现算法等时域法，Newmark法、Jacobi迭代法、最小修正量法、摄动法等频域法，神经网络算法、遗传算法、粒子群算法等演化理论方法。Ahmadian等[3]将特殊界面元素应用到机械系统结合部的建模中，将结合部处理为薄层材料，可以调整材料属性以改进系统的动力学模型，并通过模态实验识别薄层材料的弹性模型及泊松比；Eriten等[4]采用直接微动回路法和间接接触共振法两种方法直接测量了结合部的切向刚度和阻尼；Cooper等[5]最早提出了基于物理模型的递推最小二乘物理参数识别方法；Tsai和Chou[6]提出以单个零件及组装部件测试得到的频响函数识别结合部参数的方法，该方法在实际运用过程中需要三次矩阵求逆，因此识别结果对误差相当敏感；Franco等[7]改进了遗传算法中的进化策略，并将其应用于结构的刚度、阻尼及质量参数的辨识。Lu和Tu[8]将灵敏度分析及遗传算法相结合进行结构的参数识别；马蕾等[9]提出了一种基于多体系统传递矩阵法的物理参数辨识方法，应用该方法实现了平面刚柔耦合多体系统、变截面梁系统、激光陀螺捷联惯组减振系统的关键参数的准确识别；丁颖[10]运用Ansys软件建立了小孔节流空气静压径向轴承和止推轴承气膜模型，并通过Fluent软件对其进行动态仿真分析，获得了不同转速、偏心率对各向气膜刚度的影响规律；牛卫朋[11]针对MCH63加工中心联合Hypermesh和Ansys建立了融入结合面刚度和阻尼参数的机床整机有限元模型，对结合面等效建模及参数设置做了深入的理论分析，并通过对比有限元仿真和模态试验的结果验证了理论分析的正确性；李天箭[12]基于空间统计学提出了一种超精密机床刚度的多空间尺度特性解析与设计方法，通过研究超精密机床整机刚度随着各部件与部件间结合面组成的刚度链的变化而在工作空间内变化的规律，确定刚度优化设计参数。

总体而言，大多依赖有限元仿真或试验手段获取超精密机床关键部件的动力学参数。而网格质量、边界条件和接触设置等均会影响有限元仿真结果的准确性；试验则需要对关键部件单独进行，耗时久，成本高。因此，本文针对超精密机床系统提出了一种基于多体系统传递矩阵法的参数辨识方法，实现了超精密机床整机系统动力学参数的辨识与优化。首先利用多体系统传递矩阵法求出系统的固有频率，通过多岛遗传算法搜索系统的动力学参数，使系统固有频率的计算值与试验值一致，最后利用试验验证了该方法的正确性。

1 超精密机床系统固有振动特性分析

多体系统传递矩阵法是通过建立多体系统中元件状态矢量间的传递关系来解决多体系统动力学相关问题的新方法。采用该方法对复杂机械系统进行动力学研究时具有无需系统总体动力学方程，系统矩阵阶次低、总传递方程自动推导、建模灵活、计算速度快、程式化程度高等特点。

1.1建立超精密机床系统动力学模型

本文研究的超精密机床系统实物模型如图1所示，床身大多采用温度敏感度低的天然大理石材料；工作台组件采用液体静压导轨支撑，导向精度高、稳定性好；主轴系统采用气体静压轴承支撑，径向和轴向旋转精度高。

图1 超精密机床物理模型

图2 超精密机床系统动力学模型

根据机床系统各部件的材料特性、形状尺寸及部件之间的联接方式将整机系统划分成6个子系统。本文将这6个子系统均考虑成空间振动刚体，并采用空间弹性铰描述子系统间的结合面特性，由此便建立了该超精密机床系统的动力学模型如图2所示，其拓扑图如图3所示。其中，元件13是由地基和5个千斤顶组成的地基系统，元件11是由床身、立柱、横梁、导轨等部件组成的支承系统，元件1是由导轨滑台、工作台安装座、真空吸具、工件组成的进给系统，元件4是力矩电机动子，元件6是拨叉盘组件，元件8是由主轴转子、刀盘、刀架等部件组成的主轴系统；元件2、3、5、7、9、10、12、14为空间弹性铰。

图3 超精密机床系统动力学模型拓扑图

将图3拓扑图中的闭环切开，便得到图4所示的系统动力学模型树形拓扑图。其中，圆圈表示体元件，箭头表示铰元件及其传递方向，Z1,0、Z14,0为系统的固定边界，Z3,0、Z11,3、Z10,0、Z6,10为闭环切割产生的虚拟边界，且有:

(1)

图4 超精密机床系统动力学模型树形拓扑图

1.2 超精密机床系统固有振动特性分析

根据文献[13]，空间多体系统的状态矢量定义为：

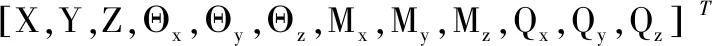
(2)

式中的元素分别为系统在单个简谐激励作用下P点处的线位移、角位移、内力矩和内力的复振幅。

根据线性多体系统传递矩阵法的自动推导定理，可以方便快捷地推导出超精密机床系统的总传递方程：

UallZall=O

(3)

式中，Uall为系统总传递矩阵，Zall为系统边界总状态矢量，是各边界状态矢量按序排列组成的一个列阵。

(4)

(5)

(6)

(7)

(8)

将系统边界条件:

(9)

代入式(3)，并整理可得：

(10)

对于系统的真实自由振动，式(10)有非零解，则其系数矩阵行列式的值应为零，即:

(11)

上式是关于系统固有频率的代数方程，即系统频率方程。该方程可利用二分法、抛物线法、弦截法、黄金分割法以及递归搜索等多种方法进行求解。元件的质量、尺寸、位置关系均可从机床UG三维模型中读取，空间振动刚体、空间弹性铰的传递矩阵可从元件传递矩阵库中找寻。

2 试验模态分析

超精密机床整机系统振动模态试验是在气阀、油阀正常工作的情况下，采用单输入单输出的方式进行，以工作台所处位置不同分为3个工况，试验现场如图5所示。首先在超精密机床某点处施加力锤激励，然后通过信号调理仪和数据采集箱依次实现机床各个测点加速度振动信号的采集，最后采用模态分析软件对所有测点试验数据进行分析，利用模态参数识别技术识别出机床的固有频率、振型等模态参数。模态试验参数设置如表1所示。

表1 模态试验参数列表

图5 超精密机床模态试验现场图

为准确描述超精密机床整体形态，共布置了224个测点，测点分布如图6所示，床身与左右导轨共82个点，真空吸具、工作台和导轨滑台共64个点，立柱与横梁共36个点，刀盘与刀架共22个点，电机16个点，地基4个点；某些方向不方便放置加速度传感器或敲击的测点，采用振动效果接近的点来等效。

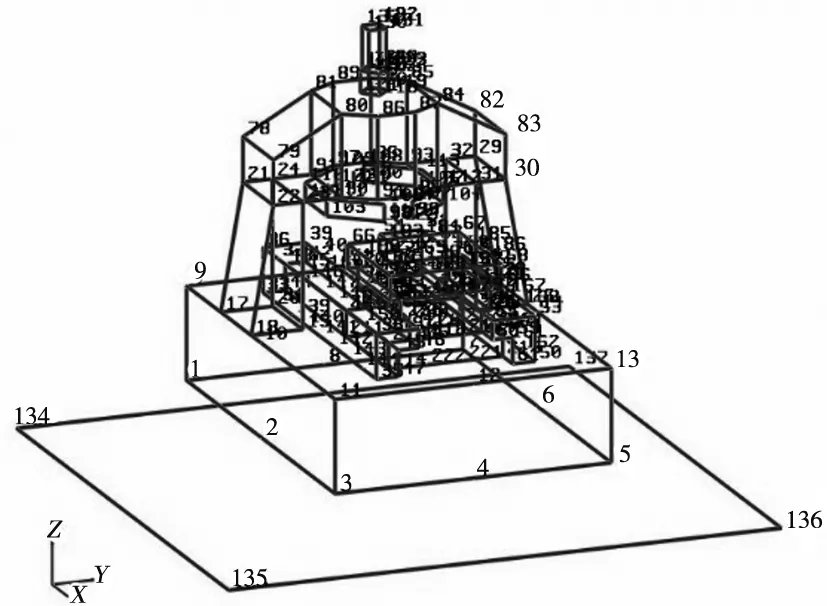
图6 超精密机床模态试验测点分布图

由于超精密机床结构复杂，测点较多，为提高试验效率，基于线性系统的互易性原理，采用固定激励点与固定测量点相结合的方法。首先固定激励点，依次测量不能进行锤击的测点的频率响应函数，然后将传感器固定在激励点，用力锤激励其他可以锤击的测点，得到测点的频率响应函数，这样便完成所有测点的测量。在测量时，始终检查测量的相干函数，保证各阶模态频率附近的相干函数在0.9以上，以确保测量数据的可靠性。否则，检查原因，重新测量，直到达到要求。

最后，采用幅频集总平均法，对测量的全部频率响应函数的幅值进行线性平均，据此估计各阶模态固有频率初始拟合值。经过大量测量数据的集总平均，可总体上反映结构在分析频率范围内共有多少阶模态，可以大大减少遗漏模态、虚假模态等情况。图7为工作台处于导轨中间位置工况下，不同方向的幅频集总平均曲线。

(a) x方向

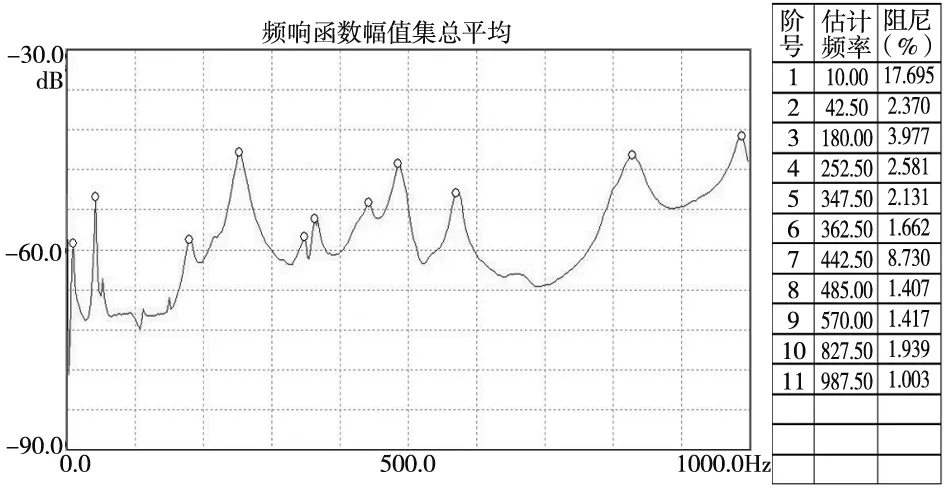
(b) y方向

(c) z方向 图7 试验幅频集总平均曲线

3 超精密机床系统动力学参数辨识

3.1 建立优化模型

由于超精密机床系统结构复杂，求解精度要求高，且涉及的参数多，采用通常的多体系统动力学方法直接求解系统的动力学参数很难实现。因此本文在已知系统实测模态参数的情况下，提出了一种基于多体系统传递矩阵法的机床系统动力学参数识别方法，该方法的总体思路如图8所示。以系统的固有频率为目标函数，采用多岛遗传算法搜索系统的动力学参数，使通过多体系统传递矩阵法计算出的系统固有频率与试验固有频率一致来实现对机床系统动力学参数的识别。

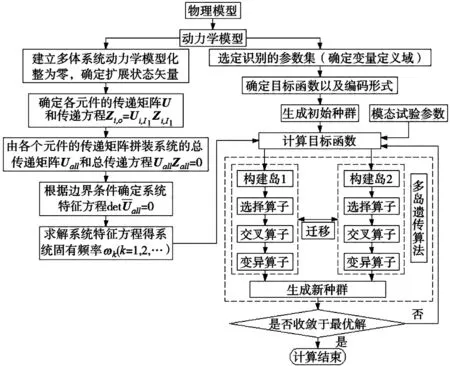
图8 超精密机床系统动力学参数辨识流程图

多岛遗传算法是在传统遗传算法基础上建立的一种基于岛屿模型的并行性遗传算法，具有更优良的全局搜索能力和计算效率。该算法是将整个种群分解成多个子种群(称为“岛”)，在每个岛上运用标准遗传算法的操作(选择、交叉、变异)对子种群独立地进行优化。并通过不同岛上的个体定期迁移的方式来保持进化过程中个体的多样性，从而有效地抑制早熟现象，有利于找到全局最优解。因此本文采用多岛遗传算法来实现复杂超精密机床系统各铰元件刚度参数的识别与优化。采用Fortran语言编译实现系统固有频率计算及多岛遗传算法的执行。优化模型中多岛遗传算法控制参数设置如表2所示。目标函数为：

(12)

表2 多岛遗传算法控制参数列表

3.2 辨识结果分析

应用上述参数辨识方法得到的参数如表3所示，将其代入到已开发的MSTMMDSim软件中计算可得到超精密机床系统的固有频率及系统振型。系统固有频率通过多体系统传递矩阵法得到的计算值、运用Workbench仿真得到的仿真值[14]以及模态试验测量值如表4所示，系统第1阶振型的计算、仿真和试验结果如图9所示。

表3 超精密机床系统动力学参数辨识结果

续表

表4 超精密机床系统固有频率(Hz)

(a) 计算

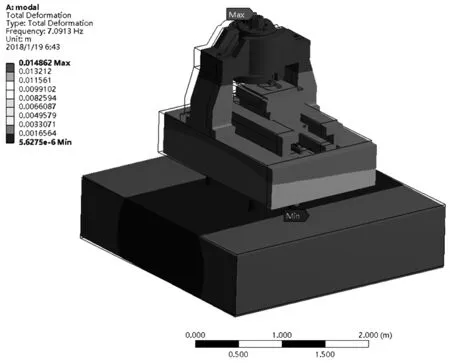
(b) 仿真

(c) 试验 图9 超精密机床系统第1阶振型

由表4和图9可知，超精密机床系统振动特性的计算结果和有限元仿真结果、模态试验结果吻合较好，验证了本文所建动力学模型和所选参数的合理性，从而证明了本文提出的参数辨识方法的可行性和准确性。

4 结论

本文建立的超精密机床整机系统动力学模型，巧妙地将机床整机结构系统中典型结合面特性转化为动力学模型中铰元件的动力学参数，简单明了；鉴于超精密机床结构复杂，系统总体动力学方程建立繁琐等问题，采用多体系统传递矩阵求解系统的固有振动特性，无需系统的总体动力学方程且计算效率高；针对超精密机床系统参数多、难求解等问题，提出了一种融合多体系统传递矩阵法与多岛遗传算法的动力学参数辨识方法，并通过模态试验有效地验证了该方法的可行性和合理性。