齿面磨损对齿轮系统动态特性的影响*

(沈阳工业大学机械工程学院 辽宁沈阳 110870)

齿轮齿面由于运行过程中受到载荷和润滑状态的影响，会出现磨损。对于新的齿轮装置来说，在最初的运行期间由于齿面相互间的摩擦力而产生的磨损经过一定时间后，会逐渐减少，这个过程称为跑合，对传动系统是无害的。但随着时间的增加，磨损会导致齿轮啮合点的变形量发生变化，从而造成轮齿的刚度发生变化，进而影响整个传动系统。据统计，机械设备故障的80%是由于齿轮系统失效引起的，其中磨损和点蚀占失效的41%。齿面磨损会降低齿轮传动的效率和精度，甚至引起严重的机械事故[1]。关于磨损，国内外一些学者对其进行了研究，主要有模型仿真计算和实验2种研究手段。胡波和黄平[3]将齿轮啮合区域的齿廓进行离散化处理,建立了齿轮齿廓磨损计算模型。冯松等人[4]在齿轮共轭啮合原理基础上，针对运行过程中的齿面磨损，提出轮齿等弧长离散方法，为研究齿面磨损齿轮动力学建模提供了一条技术路径。陈海锋等[5]通过激光共聚焦显微镜、白光干涉仪和硬度计分别对磨损严重的齿轮齿面微观形貌和表面硬度进行检测。王晓笋等[6-7]采用变步长Gill积分方法，利用Archard计算齿面动态累积磨损量,分析动载荷、动态磨损系数和滑移速度对齿面磨损影响。石万凯等[8]用Archard磨损公式结合JKR理论建立微齿轮粗糙齿面仿真模型。张俊等人[9]建立了真实工作情况的直齿圆柱齿轮准静态磨损模型。

齿面磨损会影响齿轮的时变啮合刚度等非线性因素，使得齿轮传动系统在运行中会呈现复杂的非线性动力学特征。卫一多等[10]建立包含时变刚度和齿侧间隙的单对齿轮系统振动模型, 运用四阶龙格库塔方法计算系统在无冲击 、单边冲击和双边冲击状态下系统参数和载荷参数对系统振幅及稳定性影响。ZHOU等[11]考虑时变啮合刚度、齿轮偏心、轴承等多种因素，研究不同啮合频率、不同载荷下齿侧间隙对齿轮副振动和冲击状态的影响。

以上的大多数研究都是针对齿面磨损对啮合刚度、齿廓的影响，很少有学者研究齿面磨损对啮合齿轮系统的影响。本文作者将磨损考虑进齿轮的时变啮合刚度中，采用集中参数法进行模拟并通过改变转速和运行次数的大小来研究齿面磨损对齿轮系统动态特性的影响。

1 齿轮系统非线性动力学模型

1.1 含磨损的时变啮合刚度计算

根据Archard理论[6]，齿轮传动系统运行i次时，齿轮j(j=1,2)的齿面累积磨损量Hi，j表示如式(1)所示，其中k是磨损系数；p是最大接触力；a是啮合点处的Hertz接触宽度；θj为齿轮的转角位移；Tj为齿轮的转矩；rj是分度圆半径。

(1)

p=Tj/rj

(2)

根据Weber-Banaschek公式[12]，单个轮齿的中线和啮合线交点在啮合线方向的变形量δΣj为

δΣj=δZ,j+δR,j+δpw,j+Hi,j

(3)

式中：δZ, j是弯曲、剪力产生的变形量；δR, j是基础部分变形量；δpw, j是载荷作用点到轮齿中线和啮合线交点间由于接触而产生的接近量。3种变形量的计算公式分别为

(4)

(5)

(6)

(7)

(8)

(9)

αFj=arccos(rj/rcj)

(10)

式中：Ej是齿轮的弹性模量;Bj为齿宽;α是压力角；hj是载荷作用点到轮齿中线和啮合线交点的距离;rcj是齿轮的齿根圆半径;ρj为接触点的当量曲率半径。

则轮齿的时变啮合刚度可表示为

km=p/(δΣ1+δΣ2)

(11)

1.2 摩擦力臂的计算

(12)

(13)

(14)

(15)

式中：ω1是输入角速度；ti是一个周期内齿轮系统的运行时间。

齿面间的摩擦力为

Ff=λ(vs)μFm

(16)

式中：μ是摩擦因数；λ(vs)是摩擦力的方向系数，由相对滑动速度vs决定：

(17)

Fm为齿轮副动态啮合力，表示沿齿面接触线上分布的动态啮合力，作用在齿宽中央，根据黏弹性论，其表达式为

(18)

其中：cm为齿轮啮合的啮合阻尼；δ为啮合线方向主动轮与从动轮之间的位移，可表示为

δ=rb1(ω1t+θ1)-rb2(ω2t+θ2)-e(t)

(19)

其中:ω2是输出角速度；e(t)是齿轮的啮合误差，表示为

(20)

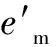
(21)

因此，摩擦转矩可表示如下：

(22)

图1 齿轮轮齿啮合示意图Fig 1 Gear teeth meshing

1.3 集中参数法建模

齿轮副系统动力学模型如图2所示。其中mj齿轮的质量；Oj是齿轮的旋转中心；ktj，ctj是轴的扭转刚度和阻尼；xj、yj为齿轮沿x、y方向的位移；Jj为齿轮的转动惯量。

图2 齿轮副扭转振动分析模型Fig 2 Analysis model of torsional vibration of gear pair

根据拉格朗日方程推导的扭转振动方程：

(23)

2 数值仿真

以江苏千鹏诊断工程有限公司生产的旋转机械振动及故障诊断模拟试验平台为例，参数如表1所示。

表1 齿轮参数

通过分析得到齿轮系统的时域、频域、相图、庞加莱和瀑布图。当不存在磨损、运行次数i=104、转速n1=1 000 r/min时，系统的响应如图3所示。由图3(a)可以看出，系统的振幅变化呈现周期性波动；在频域图3(b)中，啮合频率f(fm=n1z1/60)为主导响应，2fm仅次于fm的第二大频率，在其周围有少量较小杂频存在；相位图3(c)为规则的圆形轨迹；在庞加莱图3(d)中，所有离散点聚集在一个区域。

图3 无磨损时主动齿轮的时域、频域、相图、庞加莱图Fig 3 Time domain, frequency domain, phase diagram, Poincare diagram of the drive gear without wear

2.1 含齿面磨损的时变啮合刚度计算

图4所示为啮合齿轮对运行i=104后齿面的累积磨损量，图5所示为啮合齿轮对在运行不同次数后主动轮的齿面累积磨损量变化。

图4 主、从动齿轮的齿面累积磨损量Fig 4 Cumulative wear of the tooth surface of the main and driven gears

图5 不同运行次数下主动轮齿面累积磨损量Fig 5 Cumulative wear of the tooth surface under different running times

可以得出，齿面磨损量随着运行次数增加而增加；在啮合区域内，齿根处的齿面磨损量呈减小趋势，在节点处理论磨损量为0，齿顶处齿面磨损量呈增加趋势；齿面磨损量减小趋势大于增加趋势，即齿根处磨损现象更严重。图6示出了齿轮时变啮合刚度，齿轮齿面磨损后其时变啮合刚度幅值相比末磨损有所减小；在双齿区刚度减小量几乎为0；整个过程中齿轮的时变啮合刚度是减小的。

图6 时变啮合刚度Fig 6 Time-varying mesh stiffness

2.2 转速对含有齿面磨损齿轮系统的影响

图7所示为含有齿面磨损、运行次数i=104，主动齿轮转速分别为600、1 000、1 400 r/min时主动轮的时域、频谱、相位和庞加莱图。图7(b)与图3所示规律基本一致，而图7(b1)中的振幅小于图3(b)。以往的经验中，当齿轮传动系统不含有齿面磨损时，转速的增加会加剧齿轮传动系统的波动。n1=600 r/min时主动轮的振幅在单周期出现多个不等峰值如图7(a1)所示；图7(a2)中啮合频率fm(fm=n1z1/60)是主导频率，并能看到2fm和其他的一些杂频成分；图7(a3)中相图呈现出多个交叉的圆，说明此时系统产生了一定的波动；图7(a4)中所有的离散点聚集在一处。当n1=1 000 r/min时系统振幅波动减少,如图7(b1)所示，类似图3(a)所示。而n1=1 400 r/min时又产生一定的波动，但图7(c3)中波动幅度要小于图7(a3)。随着转速的增加，系统的庞加莱离散程度逐渐增大，振动响应逐渐增大。

图8所示为转速变化时含有齿面磨损的主动齿轮的瀑布图，主动齿轮转速在500～800 r/min的区间内系统的频域除了fm、2fm外，还有大量的杂频;在800～1 000 r/min范围内，杂频减少;当转速达到1 000 r/min后，杂频又继续增多。以上现象结合图7可以得出，在500～800 r/min内和达到1 000 r/min以后，磨损对系统的影响比较大，在800～1 000 r/min范围内对系统的影响比较小。

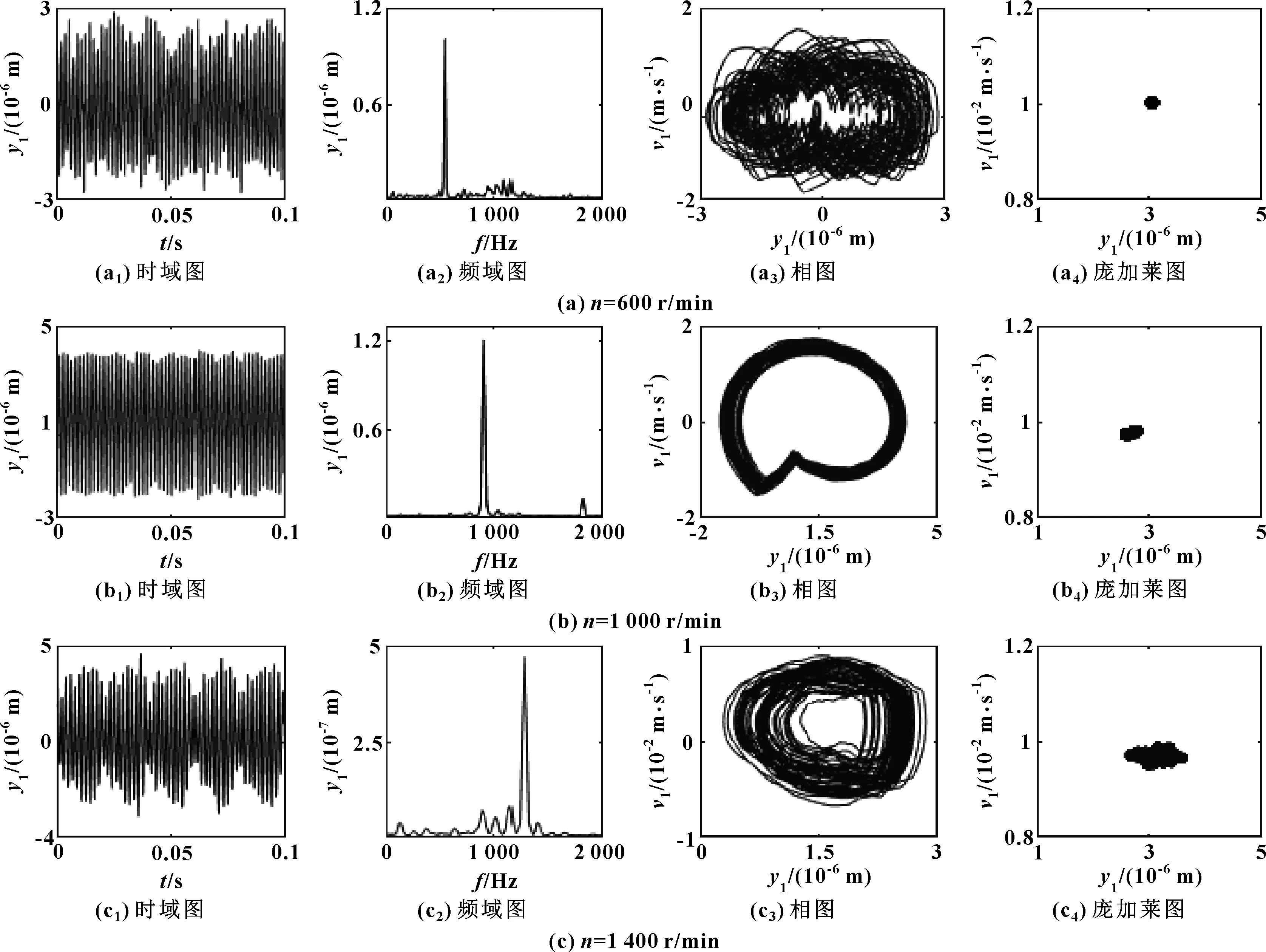
图7 不同转速下含有齿面磨损的主动齿轮的时域、频域、相图、庞加莱图

Fig 7 Time domain, frequency domain, phase diagram, Poincare diagram of the drive gear with tooth wear under different rotation speed

图8 含有齿面磨损的主动齿轮的瀑布图Fig 8 Waterfall figure of driving gear with tooth wear

2.3 运行次数对含有齿面磨损齿轮系统的影响

在以往的研究中由于不考虑齿面磨损，运行次数对齿轮传动系统几乎没有什么影响。加入齿面磨损后，随着运行次数的增加，齿面累积磨损量逐渐增加，经过一段时间后，累积磨损量会对系统产生影响。图9所示为转速n1=1 000 r/min，运行次数i=105、i=106时系统的时域、频谱、相位和庞加莱图。

图9 不同运行次数时含有齿面磨损的主动齿轮的时域、频域、相图和庞加莱图Fig 9 Time domain, frequency domain, phase diagram, Poincare diagram of the drive gear with tooth wear under different running times

与图7(b)比较可以得出随着运行次数的增加，系统的振幅也随之减小。i=105时图9(a3)、9(a4)所示的轨迹和点的离散程度，相对于图7(b3)、7(b4)没有明显变化,而i=106时图9(b3)中的轨迹明显变得更杂乱，图9(b4)中点的离散程度明显要大于图7(b4)。因此随着运行次数增加，齿面磨损对齿轮系统影响也会明显增加。

3 结论

(1)由于磨损的影响，含有齿面磨损的时变啮合刚度幅值减小，且振幅的波动性增大。

(2)在啮合区内，磨损的趋势是在齿根处先减小，在节点处理论磨损量为0，然后在齿顶处逐渐增大，齿根处的磨损程度更严重。

(3)存在齿面磨损时，随着转速的增加，齿轮系统响应的振幅逐渐增大。在500～800 r/min范围内和1 000 r/min以上，由于磨损的影响，传动系统产生一系列波动，转速在800～1 000 r/min范围内，不平稳趋势较小，选择合理的转速区间可以减少系统的波动。

(4)当磨损量较小时，i≤105时磨损对系统的影响较小，随着磨损次数达到一定的程度，磨损对系统动态特性的影响明显增加。