选择语义与反事实条件句概率浅析

展翼文

内容提要：根据Cariani and Santorio（2017）①Cariani and Santorio,“Will done Better: Selection Semantics,Future Credence,and Indeterminay”,in Mind,2017 (127),pp.129-165. 所提倡的针对will 语句的选择语义（基于选择函数而非可能世界量词的语义），本文讨论并提供了这种选择语义的反事实条件句版本。借助这一语义解释，本文继而探讨了为一种反事实条件句概率的琐碎性证明提供反例的可能性，并简要分析了接受这一反例的代价。

一、条件句概率与琐碎性

自20 世纪70 年代以来，伴随着学界对条件句语义的研究进展，人们对条件句所表达的概率的分析也开启了新的篇章。其中以大卫·刘易斯为代表，学者们提出了各种版本的关于条件句概率琐碎性的证明。简而言之，这一类证明都是针对如下被称为斯托内克命题（Stalnaker’s Thesis）的等式：

斯托内克命题：对于任意定义在语句上的概率函数Pr①这里，语句的概率函数可以理解为对语句的理性信念强度函数（rational credence），在这个意义上，斯托内克命题蕴含了对某种客观贝叶斯主义的承诺。严格地说，我们可以通过定义语句A 所表达的命题（比如一个可能世界集），以及命题上的概率函数P，来间接得到语句的概率函数Pr的定义。，对任意语句A，C，如果Pr(A) >0，那么：

Pr(A→C)=Pr(C|A)②这里的A →C 用于表示直陈条件句（而非实质蕴涵）。

斯托内克命题试图将条件句的概率同条件概率联系起来，而这在多数情况下也确实符合我们对条件句的直觉，比如下面的句子：

（1）如果这个骰子掷出了偶数，那么它掷出的点数是6。

直觉来讲，我们认为句子（1）为真的概率是三分之一，而如果斯托内克命题是成立的，我们通过条件概率对（1）前件和后件的两个子语句进行演算，也能得到同样的结果。因此，如果斯托内克命题是成立的，那这等于是向我们提供了关于条件句语义分析的一项重要而关键的工具。

然而，自从斯托内克命题被提出以来，学界针对它提出了各式各样的反例。最有名的当属以刘易斯为代表的一系列琐碎性证明。根据这类琐碎性证明，斯托内克命题只在琐碎的意义上成立。比如刘易斯指出③参见Lewis,“Probabilities of Conditionals and Conditional Probabilities”,The Philosophical Review,1976 (85),pp.297-315。，斯托内克命题只有在Pr(C|A)=1 的情形下成立，而这意味着我们在对给定条件句的概率进行分析时，实际上是将其简化为了实质蕴涵句。

虽然斯托内克本人的条件句语义①参见Stalnaker,“A Theory of Conditionals”,in Studies in Logical Theory,edited by N.Rescher,Oxford,1968。本文将在第二节对其进行介绍。并不直接涉及对直陈条件句和反事实条件句的区分，但斯托内克命题却并不能直接运用在反事实条件句之上②在语法上，与直陈条件句（indicative conditional）直接对应的概念似乎是虚拟条件句（subjunctive conditional）。“虚拟条件句”和“反事实条件句”这两个概念之间的联系和区别是相当烦琐复杂的，这里涉及许多语言学上的细节。从哲学语义学所关心的角度来说，这两个概念在某种意义上都不算十分贴切：一方面，条件句的虚拟性不必然需要通过虚拟语气来表达；另一方面，一些所谓反事实条件句未必在严格意义上是与事实相悖的。尽管如此，本文将在一般地意义上把“虚拟条件句”和“反事实条件句”当作同义词来使用。我也会在第三节对本文所涉及的反事实条件句（及其与所谓“直陈条件句”的区别）进行界定。。不过，如果对斯托内克命题进行些许改造，似乎便可以将其自然而然地运用到反事实条件句上。这里主要的想法是基于斯托内克命题与拉姆齐测试（Ramsey Test）的相似性：斯托内克命题所指向的条件概率Pr(C|A)可以看作是对后件的概率Pr(C)的条件化（conditionalization），亦即刻画了认知主体在获知A之后应该如何对其信念强度Pr(C)进行更新。而这恰恰是拉姆齐测试的想法——根据威廉姆斯（Williams）的建议③参见J.Robert G.Williams,“Counterfactual Triviality”,Philosophy and Phenomenological Research 85(3),2012,pp.648-670。，我们可以定义一种“假设性信念强度”（suppositional credence）PrA(·)=Pr(·|A)，它用于描述我们在假设某个命题（作为条件句的前件）成立时，对任意命题（作为条件句的后件）的信念强度。比如，对于句子（1），我们可以将其翻译为“假设这个骰子掷出了偶数，那么它掷出的点数是6”。通过这种对假设性的处理，我们便可以自然地对反事实条件句的拉姆齐测试给出如下描述：

反事实拉姆齐测试（CRT）：对任意Pr，A，C，如果用A□→C来表示反事实条件句“IfA，wouldC”，那么：

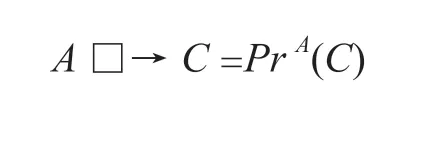
然而，正如威廉姆斯所指出的，斯托内克命题的这种在反事实条件句中的扩展也同样面临着琐碎性的挑战。本文将不会讨论威廉姆斯本人所给出的琐碎性证明，而是会关注圣托里奥（Santorio）①参见Santorio,“Collapse for Counterfactual Probabilities”,Draft,2018。所给出的另一种十分强有力的证明。圣托里奥的证明并不直接指向反事实拉姆齐测试的琐碎性，而是试图证明一种关于反事实条件句概率的“坍缩”（collapse）的结果。圣托里奥的证明仅基于几条非常弱的前提，却有着威力很大的（同时直觉上难以接受的）后果。为此，我将首先在下一节中对“坍缩性”证明所涉及的两种反事实条件句以及圣托里奥的证明结论进行简要的介绍。其次，我将在第三节给出基于选择函数的、针对“将会”的反事实条件句的语义，并在第四节中对这种语义下的反事实条件句概率的问题进行讨论。最后，我将在本文的结论中给出一种可以抵御“坍缩性”的对反事实条件句语义的解释路径并探讨接受这一路径的代价。

二、“将会”与“可能”

本节首先需要对反事实条件句的经典语义，特别是刘易斯所区分的两种不同的反事实条件句语义进行介绍。在介绍刘易斯的版本之前，让我们先来回顾一下斯托内克的基于“选择函数”的条件句语义。

（一）斯托内克选择函数与条件句语义

在讨论条件句语义的时候，人们一般会引入某种“基础模态空间”的概念。如果采用克拉泽（Kratzer）②参见Kratzer,Modals and Conditionals,Oxford,2012。颇具影响力的表达法，这种“基础模态空间”（克拉泽称之为modal base）可以用一个从可能世界到命题集的函数f:wp(w)来表达，这里的命题集便是我们评估一个语句真值时所需要考虑的（由其语境给出的）背景信息。换句话说，相对于可能世界W，由nf（W）所给出的可能世界集便对应于当我们在W上对某一语句中的模态词进行解释时，由通过其语句背景信息所确定的可及关系R所给出的那些世界的集合。

有了基础模态空间f，斯托内克关于条件句的语义便可以在其中给出，其大致可以表述为：条件句A→C在世界W上是真的，当且仅当在距离W最近的、A在其上为真的世界上C也为真。换言之，如果我们将任意一个语句Φ在其上为真的世界称之为Φ-世界，那么，条件句A→C在世界W上是真的，当且仅当距离W最近的A-世界刚好也是一个C-世界。根据斯托内克的想法，这个距离W最近的A-世界由选择函数S来负责选出。

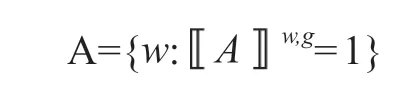
而对于必然命题“Must A”，我们需要相对于基础模态空间f对其进行解释：

此外，这里我们可以将基础模态空间f也当作语句中隐藏的索引词，因此，其函数值f(w)可以通过赋值函数g(f)给出。

最后，为了给出斯托内克的条件句语义，我们还需要定义选择函数s。函数s:w×p（w）w是一个选择函数，当且仅当它满足以下两个条件①斯托内克本人对选择函数还给出了更多的限制条件，不过这里我们只需要这两个条件。：

S1.如果A 是非空的，那么s（w,A）A，并且

有了上面这些定义，我们可以给出斯托内克对于条件句的（相对于选择函数s的）语义如下：

这里我们可以对斯托内克的条件句语义得出以下三点观察：其一，这种语义并不预设直陈条件句和反事实条件句的区别；其二，这种条件句语义与上面的必然命题“Must A”的语义不同——虽然这两种语句的真值条件都受语句所隐含的基础模态空间的影响，但后者的真值条件涉及对可能世界的（全称）量化，与此相反，前者并不涉及量化（而只是使用了选择函数）；其三，斯托内克选择函数保证了能够选出一个最近的可能世界（所谓“极限假设”），但是这一点是否符合我们对语言的直觉，特别是对反事实条件句的直觉，有着很大的争议。

刘易斯对反事实条件句的语义推翻了我们上面针对斯托内克条件句语义的全部三点观察：其一，刘易斯的语义包含了对直陈条件句和反事实条件句的区别处理；其二，他的语义涉及了对可能世界的量化；其三，他的语义并没有对“最近的可能世界”的唯一性乃至存在性做出任何承诺。①参见Lewis,Counterfactuals,Basil Blackwell,1986。由于这里不是本文的重点，本文将略去对刘易斯的论证细节的探讨。由于他放弃了斯托内克的“极限假设”，刘易斯指出，我们需要对反事实条件句提供一种超赋值分析：一个反事实条件句“如果A，将会C”（IfA,wouldC）在w上为真当且仅当C在所有距离w最近的A-世界上都为真。由于这里使用了全称量词，我们可以定义另一种反事实条件句“如果A，可能C”（IfA,mightC），记作A◇→C，它在w上为真当且仅当C在任意一个距离w最近的A-世界上都为真。因而，我们得到了两种构成对偶关系的反事实条件句：

（二）圣托里奥的“坍缩性”证明

在其2018 年的一篇论文中，圣托里奥证明了，在给定的一些预设下，would与might两种条件句的概率将会是等同的（亦即“坍缩”为同一个值）：

而鉴于刘易斯对这两种条件句的区分，这样的“坍缩性”的结果将会是无法令人接受的。

如果我们预设两种条件句的对偶关系（Dual）和反事实拉姆齐测试（CRT），以及关于would-条件句的排中律，那么便可以轻易地推导出（Collapse）。然而，圣托里奥的证明甚至并不需要预设对偶关系，相反，它只需要下面的两条非常弱的、似乎很难加以反驳的预设：

非零预设（Nonzero）：对任意Pr，如果Pr(A◇→C)>0，那么Pr(A□→C|A◇→C) >0

上限预设（Upper bound）：如果Pr(￢(A◇→￢C))＝1，那么Pr(A□→C)＝1

“非零预设”等于是说，如果某人认为“如果A，可能C”的概率大于0，那么，以此为条件，“如果A，将会￢C”的条件概率也应该大于0。“上限预设”等于是说，如果某人认为“如果A，可能C”的概率为0（即其否定式的概率为1），那么他也会认为“如果A，将会￢C”的概率为1。圣托里奥具体的证明过程和对这两条预设的讨论本文将不再赘述。这里，我仅希望展示的是，圣托里奥的“坍缩”证明所基于的这两条预设是相当弱的，而且几乎在最小程度上预设了刘易斯对反事实条件句的语义。由于圣托里奥的证明并不预设would和might两种条件句的对偶性，它并不依赖于刘易斯对两种条件句所要求的那种对一定范围内可能世界的全称量词或存在量词的使用。甚至，它并不依赖于任何具体的反事实条件句语义。相反，除了（CRT），它通过以下的两条我们对于反事实条件句概率（对任意Pr）的颇为符合直觉的假设便可得出：

假设H1 对应于“上限预设”，这里本文同意圣托里奥的观点，亦即认为对这条预设提出反驳是比较困难的。假设H2 对应于“非零预设”，如果要对其提出反驳，我们便需要证明存在这样的情况，亦即存在某种概率函数（或理性信念强度函数）使得Pr(A◇→C) >0 但Pr((A□→C)(A◇→C)) >0。本文接下来的任务，便是要说明这样一种H2 的反例的可能性及其代价。本文将指出：为H2 提出反例（并因而拒斥Collapse）是可能的，这取决于我们对反事实条件句的语义的一定的理解；但是，接受这样的反例需要付出比较高的代价。最后，本文将对这一代价进行简要的讨论。

对下一节的预告：本文所建议采用的关于would-反事实条件句的语义与刘易斯不同，而是更接近斯托内克的使用选择函数的条件句语义。使用选择函数来刻画的条件句语义仍然是模态的，但是不涉及对给定范围内可能世界的量化。然而仅仅诉诸选择函数还不足抵御“坍缩性”，因为正如我们上面看到的，圣托里奥的“坍缩性”证明并不预设两种反事实条件句的对偶性。而我们所希望反驳的假设性条件H2 本身也并不涉及超赋值和量化。因此，如果要通过反对量词来拒斥H2，我们必须对基于选择函数的would-反事实条件句的语义进行更为仔细的说明。这便是下一节的主要任务：首先，我将对反事实条件句和直陈式条件句的语义学上的区别进行简要的讨论；其次，我将在这一区别的基础上给出一种基于选择函数的would-反事实条件句的语义。

这里需要说明的是，下一节所要处理的这两个任务都是十分艰巨且富有争议的任务，无论是本文的篇幅还是笔者的能力都决定了无法对这两个任务中的任何一个进行充分而细致的讨论。本文的意图仅在于有选择性地对这一课题近年来的某些理论进展加以采纳，并通过对这些理论进路的简要刻画，试图展示出它们在一般意义上的琐碎性问题图景中的应用潜力。

三、非量词的“将会”

（一）关于“直陈”与“反事实”

关于直陈条件句与反事实条件句的区别，可以通过以下两个典型的句子作为例子来进行对比：

（2）如果奥斯瓦尔德没有刺杀肯尼迪，那么有别人刺杀了他。

（If Oswald didn’t shoot Kennedy,someone else did.）

（3）如果奥斯瓦尔德没有刺杀肯尼迪，那么有别人将会刺杀了他。

（If Oswald hadn’t shot Kennedy,someone else would have.）

一般来说，句子（2）是说话者在条件句前件及其所掌握的事实性证据的假定的基础上，对现实世界的历史究竟如何的一种表述。而句子（3）则是说话者在条件句前件及其相应的反事实假定的基础上，对世界本将会怎样所做出的表述。①参见Kratzer,Modals and Conditionals，第2 章。这里，我们或许可以将前一种条件句称为是“知识性”（epistemic）的，而将后一种条件句称为是“形而上学”（metaphysic）的，并将这一区别作为我们在模态上区分直陈和反事实两种条件句的关键指征。②支持使用这一术语的典型代表如Khoo 的“On Indicative and subjunctive Conditionals”。这里需要指出的是，在笔者看来，对“知识性”条件句和“形而上学”条件句的这一区分尽管比较准确地指向了上面两种条件句之间的本质区别，但这一区分的术语选择有其潜在的误导性：虽然所谓“知识性”的条件句（2）似乎的确没有形而上学意涵，但反过来似乎并非如此——诚然，形如（3）那样的所谓“形而上学”条件句的意图确实并不在于对事实给出描述，这却并不意味着它一定是“非知识性”（non-epistemic）的。（Khoo 在其论文的脚注5 中也承认了这一点。）正如我们稍后将会看到的，如果我们不采纳刘易斯的反事实条件句的语义，而是采取一种以选择函数为基础的语义，那么这一选择函数的本质其实是基于说话者已有的知识状态而对可能世界进行选择（并相应地分配信念强度），而不是基于某种“客观的”，属于可能世界内禀性质的特征来对世界进行挑选。在这里，我们可以采用孔多拉夫蒂（Condoravdi）的建议①参见Condoravdi,“Temporal Interpretation of Modals”,in The Construction of Meaning,edited.by Beaver et al.,2002,pp.59-88。，通过对时态的分析来刻画这两种条件句的区别。我们在这里必须区分时态的两个维度：

第一个维度是狭义的、简单的时态，我们可以将其称之为“视角”（perspective）。比如说，句子（2）属于现在时视角，亦即说话者是在其自身所处的时间t上针对世界w的历史进行表述。而与此相反，句子（3）属于过去时视角，亦即说话者是在比自身所处时间t更早的某一时刻t'上进行表述。根据孔多拉夫蒂的观点，这一维度的时间视角仅仅涉及对时间索引词的移动操作，而不涉及任何模态操作。②因此，根据我们这里所采用的观点，句子（3）中说话者的过去时视角是一个纯粹时间上的操作。与此相反的观点参考比如Iatridou,“The Grammatical Features of Counterfactuality”,Linguistic Inquiry,2000 (31),pp.231-270。根据她所持有的观点，句子（3）中说话者的过去时视角实际已经引入了针对不同的可能世界的模态的操作。

第二个维度是派生意义上的、广义的时态，我们可以将其称之为时间的“导向”（orientation）。还以上面的两个句子为例，句子（2）虽然是现在时视角，但由于它所谈及的是过去的事态，因而我们可以将其称之为是“过去导向”的。与此相反，句子（3）虽然是过去时视角，但是由于它是在讨论t'时刻之后的可能情形，因而我们可以将其称之为是“未来导向”的。根据孔多拉夫蒂的观点，语句在时间导向的意义上才涉及模态操作——这样的语句或者通过模态表述世界的历史可能是如何的（关于过去的模态），或者通过模态表述世界的未来可能是如何的（关于未来的模态）。

根据这样的观点，我们可以将反事实条件句界定为这样的句子：它们具有过去的视角和未来的导向。这样的处理刚好也与英语等语言中通过过去将来式（比如用would）来表达反事实条件句的现象相吻合。③值得一提的是，这里的讨论都是以英文为工作语言所展开的，但哲学中，这类讨论都预设了关于反事实条件句的过去视角和未来导向的刻画的侧重点是在一种哲学式的、可以被普遍化的语义层面，而并不真的依赖于某一语言的具体语法现象。比如说，语言学界中似乎已有大量关于汉语句法中的反事实标记的讨论，可参见Qian Yong,“Typological Stage of Counterfactuals in Chinese”,in 27th Pacific Asia Conference on Language,Information,and Computation,2013,pp.329-338 等。这里使用的抽象术语也刻意回避了语法学中关于体貌（aspect）、语气（mood）之类的对应概念。在这里，我们可以进一步采纳克拉泽对条件句所采用的“限定者”（restrictor）分析①参见Kratzer,Modals and Conditionals,第2 章。，亦即认为条件句前件的if-从句实际上是对后件子语句中隐藏的模态词（即第二节中提到的基础模态空间函数‘f’）的限定。根据这种分析，句子（2）可以被分析为：

MODALRestrict(PAST (有别人刺杀肯尼迪))

而句子（3）可以被分析为：

PAST(MODALRestrict(PAST(WOLL (有别人刺杀肯尼迪))))

这里的MODALRestrict指代的是条件句前件对基础模态空间的限制条件（即在某个过去时刻t'，奥斯瓦尔德没有刺杀肯尼迪）。WOLL 指代的是条件句后件的未来导向，它可以是在某个过去时刻t'上通过would来表达，也可以在说话者当下的时刻t上通过will来表达。因此，对于下面这样的、英文中用简单将来时（will）所表达的句子，我们可以说它是具有现在的视角和未来的导向：

（4）如果张三投掷这枚硬币，那么它将会正面朝上落地。

（If John tosses this coin,it will land on heads.）

而根据对未来导向表述的模态化解释，这样的will简单将来时句子实际上也是一种与would类似的模态表达，而非单纯的时态表达。这也是包括孔多拉夫蒂在内的很多学者所支持的观点。②参见Condoravdi,“Temporal Interpretation of Modals”,in The Construction of Meaning,edited by Beaver et al.,2002,pp.59-88;Cariani and Santorio,“Will done Better: Selection Semantics,Future Credence,and Indeterminay”,Mind,2017 (127),pp.129-165；Kaufmann,“Conditional Truth and Future Reference”,Journal of Semantics,2005 (22),pp.231-280。简而言之，我们可以认为英文中的will=PRESENT+WOLL，而would=PAST+WOLL。

妊娠期急性脂肪肝作为特有的妊娠期疾病，主要发生于中晚期妊娠，目前临床医学对妊娠期急性脂肪肝的病因、具体发病机制仍未完全明确[8]；相关研究认为与妊娠晚期患者体内的激素水平发生改变有关，因妊娠能导致雌激素等相关激素表达水平显著升高，造成脂肪酸相关代谢出现障碍，使游离的脂肪酸堆积于患者的肝细胞、脑部及肾脏等相关器官内，引起多器官损伤，影响妊娠结局，危害母婴健康[9-10]。因此，及早发现、诊断并实施有效治疗，适时终止妊娠，对改善预后具有重要意义，但临床医学针对妊娠期急性脂肪肝并发多器官功能损害尚无特效疗法，多以对症治疗、控制病情进展为主，但疗效及预后欠佳[11]。

我们不妨在这里对“导向性”概念和可能世界模态之间的关系作一下澄清。为了引入时间性，一种办法是向基础模态空间函数引入时间参数，记为f(w,t)。①基础模态空间函数的时间参数并不影响我们对命题本身视作是可能世界集的传统定义，因此这里可以暂不涉及关于命题的时间主义（temporalism）和永恒主义（eternalism）的争论，对于这一争论本文可以保持中立。如果采纳这一做法，那我们可以说在世界w和某一时刻t，∩f（w,t）给出了所有直至时刻t的与世界w没有分别的（但在t以后的未来时刻可能不同的）世界的集合。如图1 所示：②关于时间分叉的讨论可参见Rumberg,“Transition Semantics for Branching Time”,Journal of Logic,Language and Information,2016 (25),pp.77-108。

图1 时间分叉示例

由此，f为语句给出了在某个给定的世界w和时刻t上的WOLLf的基础模态空间。③这里需要说明一点：为了将过去导向和未来导向区别开来，Khoo 区分了两种不同的基础模态空间：他将所有类型的过去导向的语句（比如［2］那样的条件句等）的基础模态空间称之为“信息的基础模态空间”（informational modal base），记为fI。在某个给定的世界w 和时刻t，fI 给出了某个说话者在w 和t 上已知的信息（即该说话者基于其所有的事实证据而可以相信为真的命题集）。相应地，他将所有未来导向的语句（包括[3]那样的反事实条件句和[4]那样的现在将来时所表达的语句）所依赖的基础模态空间称之为“历史的基础模态空间”（historical modal base），标记为fH。在某个给定的世界w 和时刻t，fH 给出了那些在所有在w 上为真的，但未必会在时刻t 之后持续为真的命题集。（参见Khoo,“On Indicative and subjunctive Conditionals”,in Philosopher’s Imprint,2015[15]）Khoo 的这一做法是为了把所谓“知识性”的和“形而上学”的条件句区别开来。然而，正如我在本书第185 页注释②中所指出的，如果我们对未来导向的模态句子或条件句不作可能世界的全称量化，这样的区别就变得没有必要了。其实，在笔者看来，没有理由认为说话者在某一时刻t 所表达的未来导向的句子所依赖的基础模态空间是不受到说话者在该时刻所掌握的已知信息的限制的，而这也符合克拉泽引入基础模态空间这一概念的初衷。（虽然她同意句子［2］和句子［3］涉及不同类型的模态表达，但在其2012 年的专著中，克拉泽明确承认仅仅依靠基础模态空间这一概念是很难做出这一区分的。参见Kratzer,Modals and Conditionals,pp.23-24。）根据以上的例子，我们可以说w1，w2，w3，w4∈∩f（w1，t1），但仅有w1,w2∩f（w1,t2）。如果说话者身处t1，那么他所使用的will-语句的基础模态空间可以是{w1，w2，w3，w4}。如果说话者身处w1,t3，那么他所使用的would-语句的基础模态空间需要通过确定某个具体的t3之前的时刻方能确定。而反事实条件句的前件可以帮助我们完成这一点——通过前件对基础模态空间的限定，我们可以确定说话者所指向的过去不应晚于某个具体时刻。以句子（3）为例，假如在t1之前的基础模态空间中的所有世界即便在引入“如果奥斯瓦尔德没有刺杀肯尼迪”的假设之后也是完全等同的，但t2不是，那么句子（3）的基础模态空间应该在t1上给出。同时，假定“奥斯瓦尔德刺杀了肯尼迪”在w1和w2上都是真的，那么由于句子（3）的前件限定，我们应当将w1和w2从其基础模态空间中排除出去。接下来，就让我们对这样句子的语义加以更加仔细的考察。

（二）反事实条件句的选择函数语义

这里需要说明的是，对于上一节中提到的关于时间分叉的理论框架，我们这里只需要利用其语义学的部分，在我们提到两个世界w1和w2在某个时间t之前是全同的，我们只是在比较天真的意义上谈及这一特性，而不需要对其相关的形而上学意涵做出任何承诺。比如，在形而上学上，我们似乎需要保持未来的“开放性”，不能说我们在时刻t就能决定未来的世界（或世界的集合）将会是怎样的。麦克法兰便认为这构成了为他所主张的相对主义语义学提供辩护的一个理由。①MacFarlane,Assessment Sensitivity,2014,第9 章。本文可以对这些争论保持中立的理由在于，我们的语义其实并不涉及对基础模态空间内历史上全同但未来可能不同的世界的全称量化。这里，本文借鉴了卡里安尼和圣托里奥（Cariani and Santorio，2017）关于will-语句的观点——根据他们的观点，句子（4）所涉及的恰恰是一种使用选择函数，而不使用对可能世界的量词所刻画的模态表述。本文认为，他们基于斯托内克选择函数的语义可以被移植到处理反事实条件句上来。

首先给出卡里安尼和圣托里奥关于will-语句的语义：

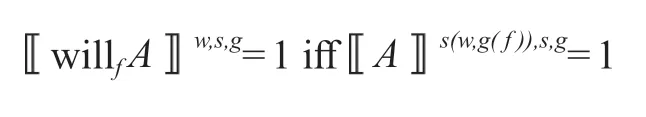
他们对选择函数s的定义也是通过S1 和S2。根据S2，如果will-语句没有嵌套在其他语句之内，那么选择函数s选出的就是w自身，因此上面右侧的充要条件其实就等于Aw,s,g=1。在这种情况下，语句中的will表达其实在语义上没有产生任何实质性的作用（对比“她明天来”和“她将会明天来”）。

然而在条件句中，由于句子的前件会对基础模态空间产生限定，这里的选择函数便发挥了实质性的作用。考虑下面的句子：

（5）如果还买得到票的话，她将在周四抵达。

（If ticket can still be purchased,she will arrive on Thursday.）

而根据条件句的限定者分析，我们便可以为这一语句给出如下语义：

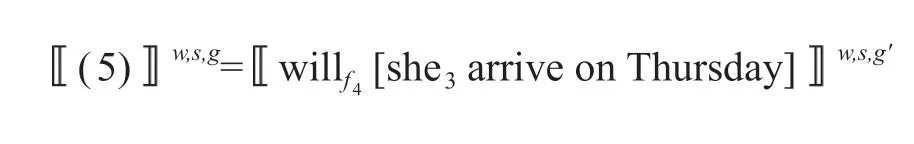
这里的g'与g仅在g'（4）≠g（4）这一处不同：

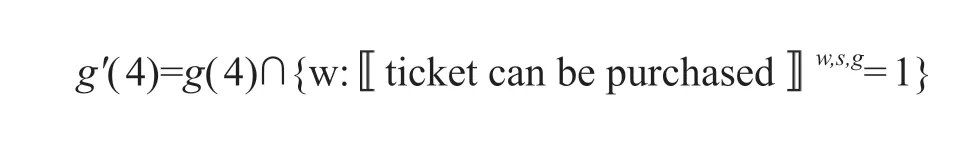
有了卡里安尼和圣托里奥的工作，我们接下来的工作其实很简单，基于前面论及的时间分叉式的关于would=PAST+WOLL 的理论假设，我们很轻松便可以将上面的选择函数的will-语义移植到反事实条件句上来。我们先定义一般性的，涉及未来导向表达的语句的真值条件语义（相对于说话者所在的时间t，而选择函数s的定义保持不变）：

考虑句子（5）所对应的反事实版本：

（6）假如当时还买得到票的话，她本将会在周四抵达。

（If ticket could still be purchased,she would have arrived on Thursday.）

（6*）[PAST[If ticket can be purchased]]4 PAST [[she3 arrive on Thursday]].

我们可以给出句子（6）的语义：

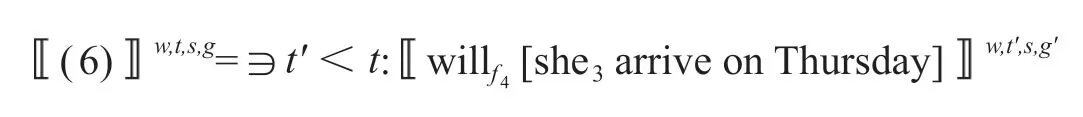
同样地，这里的g'与g仅在g'（4）≠g（4）这一处不同：

这里值得注意的是，由于句子（6）的反事实特点，经过句子前件限定后的基础模态空间g'(4)将不再包含说话者所处的现实世界w，因此，根据选择函数的定义S1，s（w，g'（4））不会选出世界w。

此外，这里我们还可以得出一个本文的重要结论：明显地，根据上面的选择函数语义，用“将会”（would）表达的反事实条件句将与刘易斯的处理不同，这里的语义将不会包含对可能世界的全称量词。

四、反事实条件句的概率问题

（一）选择函数语义下的反事实条件句概率

经过上面的准备，我们现在终于可以回到反事实条件句概率的讨论上来了。正如第二节所提到的，为了避免“坍缩性”的结果，我们需要证明存在某种概率函数（或理性信念强度函数）Pr，使得Pr(A◇→C) >0 但Pr((A□→C)∧(A◇→C)) >0。我们前面只是对使用would表达的反事实条件句（即A□→C）给出了非量词的语义，而并没有涉及might-语句。但是至少，根据这样的语义我们事实上已经放弃了两种反事实条件句的对偶性。但是放弃对偶性本身并不足以避免“坍缩性”结果（正如前面介绍的，圣托里奥的证明是基于比对偶性更弱的预设）。这里，借助前面的选择函数语义，我们可以更清楚地看到这一结果。考虑句子（4）的一个反事实变体：

（7）假如张三投掷这枚硬币，那么它本将会正面朝上落地。

（If John had tossed the coin,it would have landed on heads.）如果我们接受时间分叉式的关于would=PAST+WOLL 的理论假设，同时还对未来的可能世界的“开放性”的形而上学特征有所承诺的话，其实我们很难解释，一个关于未来的可能世界的命题的概率究竟是什么意思。①相关讨论参见Cariani and Santorio,“Will done Better: Selection Semantics,Future Credence,and Indeterminay”,Mind,2017 (127),p.15f.等。何况，且不论关于未来“开放性”的复杂争议，如果基于刘易斯式的对未来最接近的可能世界的全称量化语义的话，句子（7）直接就被该语义解释为是假的好在我们的语义是基于选择函数的，因此并不涉及对未来可能世界的全称量化。让我们考虑句子（7）所表达的命题A7：

我们对句子（7）的信念强度应该等于命题A7 的概率。但是A7 的概率应该是多少呢？我们来考虑一个极简的例子：假如我们在过去时刻t'的基础模态空间中只有三个世界w1，w2，w3，其中w1是张三掷了硬币且硬币正面朝上落地的世界，w2是张三掷了硬币但硬币背面朝上落地的世界，而w3是说话者所在的现实世界，亦即张三其实并没有抛掷硬币的世界，如图2 所示：

图2 选择函数在w3 上的不确定性

命题A7 的外延取决于句子（7）语义中的选择函数是怎样的——然而，这。里有两种可能的选择函数s1和s2①这里我们把si (wj,(∩f(wj,t'))∩toss)简单记作si (wj,T)。：

在这个例子中，虽然说话者对自己所在的现实世界是确定的，但是他对这句话应该采用哪种选择函数也许并不确定。这里一个比较严重的后果在于，即便我们假设张三可能抛掷的那枚硬币是一枚十分公平的硬币，因而其出现正面和背面的机会是均等的，但是基于我们对句子（7）所表达的命题A7 的定义，命题A7 的概率或者是2/3（如果采用选择函数s1的话是P({w1,w3})）或者是1/3（如果采用选择函数s2的话是P({w1})）。但是我们直觉上认为句子（7）的概率应该是1/2。②参见Cariani and Santorio,“Will done Better: Selection Semantics,Future Credence,and Indeterminay”,Mind,2017 (127),pp.30f。这里的问题非常类似于Hájek 提出的“墙角花”（wallflower）证明，参见Hájek,“Triviality Pursuit”,Topoi,2011 (30),pp.3-15。

此外，这样的结果似乎也并没有帮助我们摆脱“坍缩性”结论。不过这里，我们通过上面的例子却可以做出一个重要发现，即可能世界（的集合）的概率和说话者所采用的选择函数的概率某种意义上似乎可以是独立开来的。而这正是布拉德利（Bradley）的主旨③Bradley,“Multidimensional Possible-World Semantics for Conditionals”,The Philosophical Review,2012(121),pp.539-571.。我们上面已经看到了说话者针对选择函数的不确定性，此外，选择函数和可能世界彼此间的概率独立性还通过反过来的例子可以得到进一步的确证：在他的那篇论文中，布拉德利给出了与图2 所展示的不确定性不同的另一种不确定性，亦即在某种情况下，说话者即便对应该采用哪种选择函数是确定的，但却对他所身处的世界是不确定的。

这一情况可以从下面的例子给出：假定我们知道张三可能投掷的那枚硬币实际上是不公平的（比如它或者两面都是正面，或者两面都是背面），但是我们不知道究竟是这两种情况中的哪一种，如图3 所示：

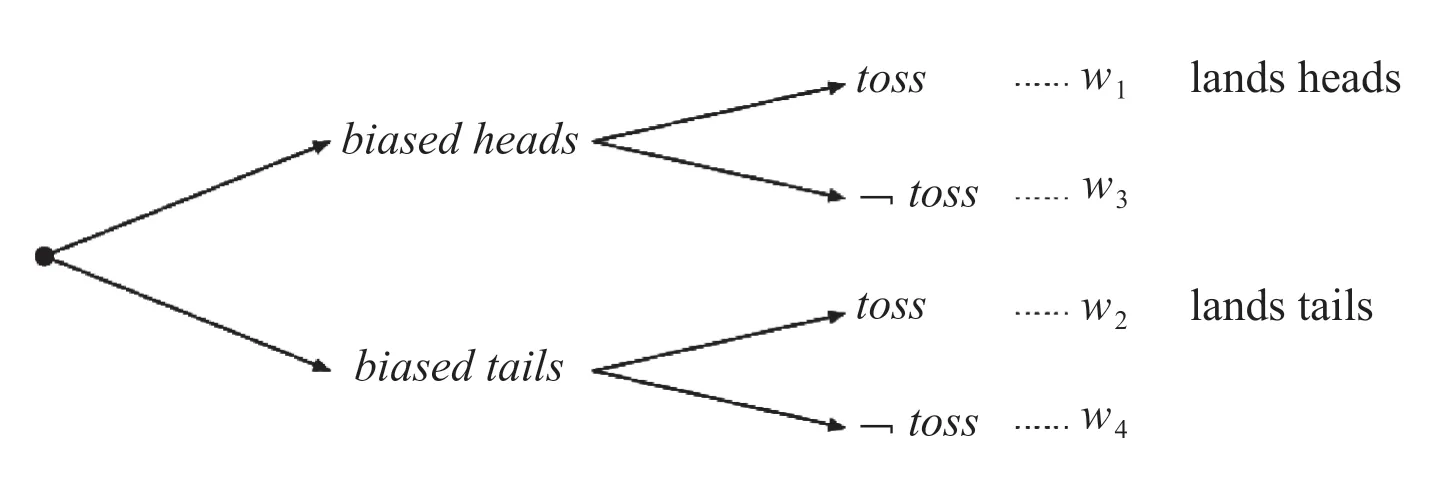
图3 世界本身的不确定性

在这样的情形下，我们对需要使用的选择函数是确定的。我们应该使用的选择函数在所有硬币两面都是正面的世界上都应该选出w1，而在所有硬币两面都是背面的世界上都应该选出w2，亦即下面的这样一个选择函数s：

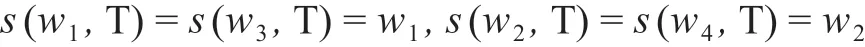
但现在的问题是，我们并不知道自己究竟是身处w3和w4中的哪一个世界。当然，我们或许可以通过一些事实证据来确定我们所处的现实世界究竟是哪一个，但是布拉德利这里的例子却似乎说明，这些事实证据与支持我们对选择函数进行选择的那些证据可以是彼此独立的。这也意味着，如果我们坚持认为反事实条件句确实是有真值条件的，那么它的真值条件似乎并不仅仅来源于某一单一维度下的事实。

（二）条件句概率与二维语义

出于以上的考虑，我们可以重新定义一种二维的反事实条件句的命题内容。仍以句子（7）为例，它的二维命题内容A7+将被定义为是可能世界与选择函数二元组的集合：

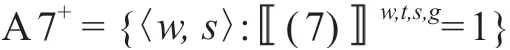
有了这一命题定义，我们便可以区分两种不同的概率函数：一种概率函数仍然是在可能世界上的，而另一种概率函数则是定义在选择函数s之上的，而反事实条件句的概率便属于这后一种。

在上一小节中，我们已经看到了区分两种不同的概率函数的一般性的考量——因为确定现实世界和确定选择函数本身是两件事。当然，在句子（7）所涉及的例子中，如果我们对自己身处的世界是确定的（如果我们身处图2中的w3），那么我们可以基于某种已掌握的事实证据来确定选择函数。比如说，如果我们知道张三的硬币是公平的，那么掷出正面朝上（w1）和掷出背面朝上（w2）的概率应该各为1/2。因此，我们可以反过来确定在w3上，说话者采用选择函数s1抑或是s2的概率也是均等的，亦即各为1/2。但在某些情形下这一方法未必适用，由于对选择函数本身的选择有可能是依赖于说话者对现实世界的确切知识的，但由于说话者事实证据的有限性，她也许恰好并不能确定这一点。

这并不意味着我们对选择函数的决定机制只能是语用的而非语义的。正如我们可以区分关于可能事实的客观概率（亦即所谓机会“chance”）和关于客观概率陈述（即事实证据）的真值的主观概率那样①参见Lewis,“A Subjectivist’s Guide to Objective Chance”,in Studies in Inductive Logic and Probability,edited by Jeffery,Vol.II,Berkeley,1980,pp.263-293。，我们或许也可以在同样意义上对定义在可能世界上的概率函数和定义在选择函数上的反事实条件句的概率函数进行区分。在理想状况下，我们由不同的选择函数所确定的反事实条件句的总体概率应该保证对这些选择函数的概率分布遵守刘易斯所谓的“校长原理”（Principal Principle）。②Ibid.但这只是理想的情况。图2 对应的例子里我们已经确切知道张三的硬币是公平的，在其他条件均同的情况下，给选择函数s1赋以1/2 的概率似乎是唯一的理性选择。但有时候我们可能有不同的关于事实证据的判断。图3 的例子便是这样，虽然这时候选择函数实际上已被确定了，但我们对现实世界究竟是w3还是w3却不清楚。虽然全局地看，“投掷这枚硬币正面朝上的概率为1/2”确实是合理的论断，但从反事实条件句的语义来看，这里其实是涉及了语义的模糊性：如果现实世界是w3，硬币正面朝上的概率实际上是1，而如果现实世界是w4，硬币正面朝上的概率实际上是0。这似乎便违反了“校长原理”。①这一现象其实也可以用主观概率和客观概率的语言来描述：不论我们身处w3 还是w4，在考虑“投掷硬币正面朝上的概率为1/2”这一命题时，我们认为该命题为真的概率为0——因为客观的事实依据是，由于我们知道硬币的两面是一样的，因此投掷硬币正面朝上的概率或者为1，或者为0。虽然主观上我们可以认为硬币正面朝上的概率是1/2，但这不意味着“投掷硬币正面朝上的概率为1/2”这个命题本身是真的，恰恰相反，在任何一个世界上该命题都是假的。对此，布拉德利在“Multidimensional Possible-World Semantics for Conditionals”中给出了一种改进版的，仅针对反事实假定的校长原理，因为篇幅所限，这里不再赘述。

五、结论

最后，我们可以试图提出一个为（H2）提供反例（并因此抵御“坍缩性”结果）的可能的方法②本文并不认为这是唯一的为H2 给出反例的方法，这只不过是本文目前能想到的最自然的一种解释路径。：如果我们保留“可能”（might）条件句的存在量词语义，而对“将会”（would）条件句作选择函数语义的解释，那么上一节中提到的would-条件句语义的模糊性便为我们提供了线索。我们可以找到这样一个概率函数Pr，使得would-条件句的概率为0，而其对应的might-条件句的概率不为0。具体举例而言，比如图3 的例子，令Pr在would-条件句中对应于选择函数概率，而在might-条件句中对应于可能世界的概率。假定在某种语境下我们可以局部地断定现实世界为w4，那么根据本文给出的反事实条件句的选择函数语义，由于硬币双面都是背面，我们可以认为句子（7）是假的（因为不会选出w1，所以概率为0）。但是全局地来看，我们或许又需要考虑硬币并非双面都是背面的情形（亦即现实世界未必是w4，也可能是w3的情形，这时候就需要考虑w1的可能性），假定might-条件句总是与涉及全局的语境相关联的，那么在这种情况下，与（7）对应的might-条件句的概率便大于0。

这样的反事实条件句语义依然是有真值条件的，只不过由于这里诉诸了would-条件句语义的模糊性，这种真值条件将不仅仅涉及事实证据，而且也可能涉及高阶证据等。①这里运用了基础模态空间“局部”和“全局”之间的差异性，这一差异性在关于条件句概率的研究中已经得到不少体现，经典的讨论参见Kaufmann,“Conditioning against the Grain”,Journal of Philosophical Logic,2004 (33),pp.583-606。针对这一点，Khoo 认为我们不应该满足于对条件句概率做出诉诸（局部/全局的）模糊性的处理。为此，他向选择函数引入了一个新的限制，要求选择函数必须在一个固定的可能世界集上才有定义（比如要求选择函数的输入和输出必须固定在一个类似{w2，w4}这样的集合上）。但是，Khoo 的这一办法并不能直接解决本文图3 例子中的模糊性，因为这里的模糊性不在于选择函数本身而恰恰在于世界的不确定性。但是，我们也看到，这种反例的代价是事实上违背了“校长原理”。此外，这里我们虽然把“IfAwould notC”和“IfAmightC”赋以类似的非零概率，但如果在同一语境下同时断言这样的两个句子仍然是不当的“infelicitous”，这也是十分昂贵的一个代价。本文更为合理的结论，应该是看到我们仍然亟需对反事实条件句的语义，特别其可能的多义性与其来源进行进一步深入的研究。②笔者衷心感谢黄禹迪、李麒麟、裘江杰、吴小安、詹伟伦在本文构思和写作过程中给予的帮助和建议。