圆锥曲线离心率的求解策略
廖永福
(福建省厦门第二中学 361009)
离心率是圆锥曲线的一个重要性质,求圆锥曲线的离心率是解析几何中的重要题型,也是高考数学的高频考点.下表给出了近5年全国卷考查离心率的情况,其中文5表示文科数学第5题.本人对近几年高考试题进行了认真的分析、归纳和整理,总结出求圆锥曲线离心率的几种有效策略,阐述如下,希望对广大师生有所帮助.
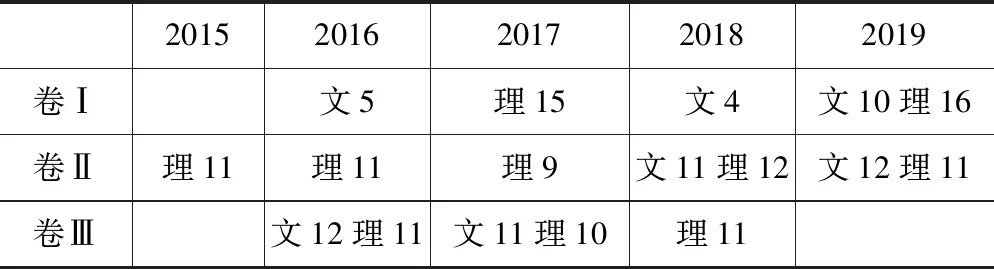
20152016201720182019卷Ⅰ文5理15文4文10理16卷Ⅱ理11理11理9文11理12文12理11卷Ⅲ文12理11文11理10理11
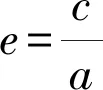
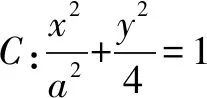
分析由已知c=2,求出a,就可以求出椭圆的离心率.
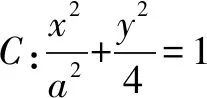
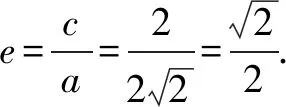
点评本题考查椭圆简单性质的应用,考查计算能力.
例2(2018·新课标Ⅱ文11)已知F1,F2是椭圆C的两个焦点,P是C上的一点,若PF1⊥PF2,且∠PF2F1=60°,则C的离心率为( ).
分析设椭圆的焦距为2c,利用已知条件求出|PF1|和|PF2|,根据椭圆的定义列出关于a、c的方程,即可求出椭圆的离心率.

图1

点评本题考查椭圆的简单性质的应用,考查计算能力.

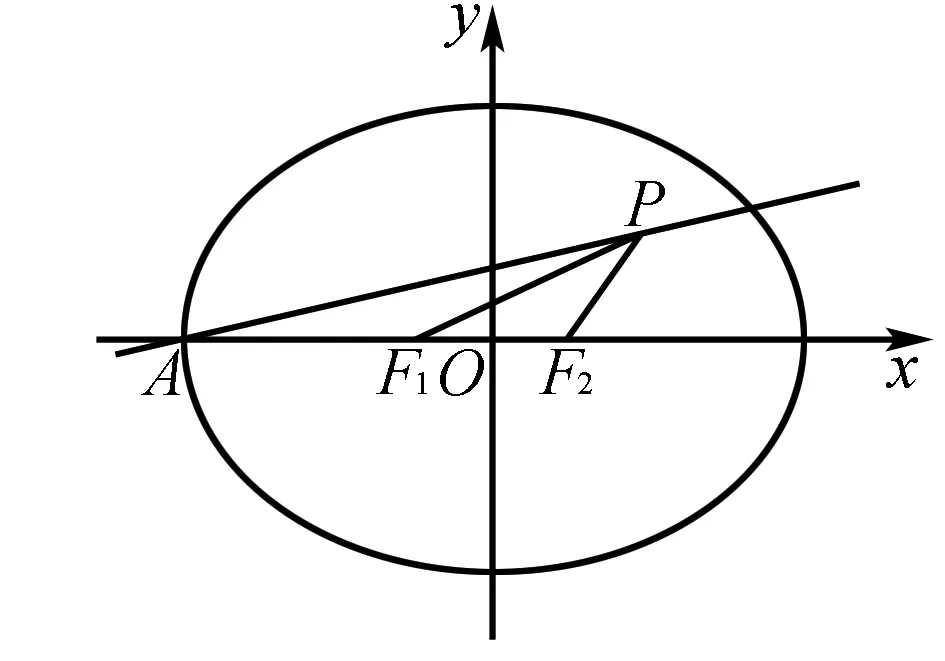
图2
分析根据题意求出直线AP的方程和点P的坐标,再把点P的坐标代入直线AP的方程,得到关于a、c的方程,即可求出椭圆的离心率.
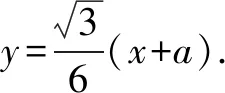
点评本题考查椭圆的性质,直线方程的应用,考查转化思想,属于中档题.

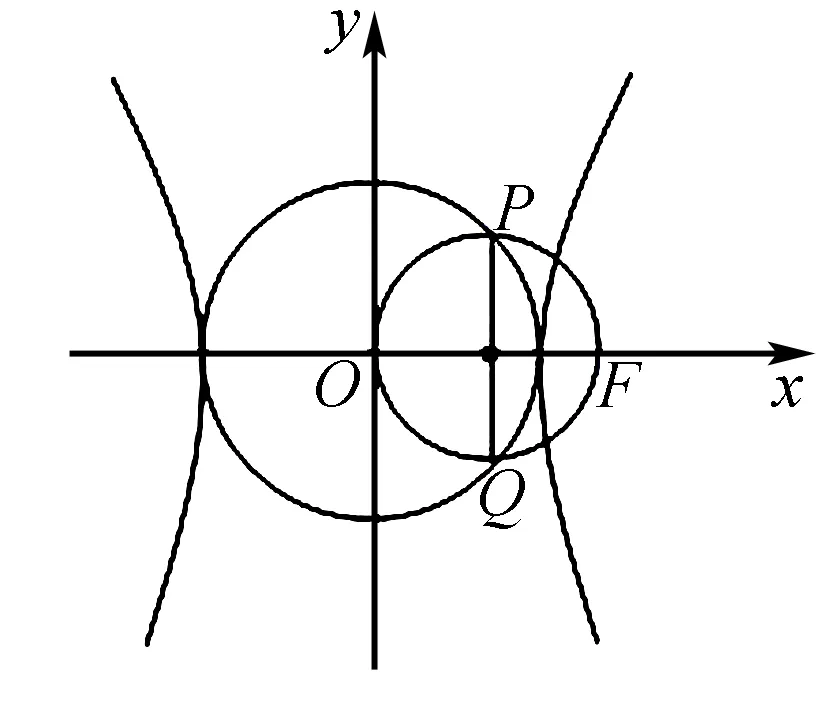
图3
分析画图,根据图形特征找出相等关系,列出关于a、c的方程,即可求出椭圆的离心率.
解答如图,连结OP、PF、FQ、QO,由题意知PQ和OF互相垂直、平分且相等.

点评本题考查双曲线和平面几何的简单性质,考查数形结合的解题思想方法,是中档题.


分析同例3.
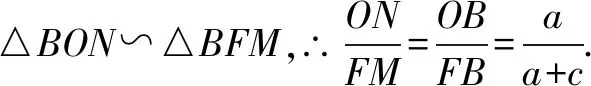


点评本题考查椭圆和平面几何的简单性质,考查数形结合的解题思想方法,是中档题.
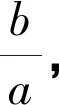

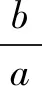

点评本题考查双曲线的简单性质,考查同角三角函数基本关系式的应用,是基础题.
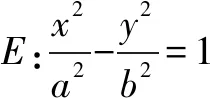

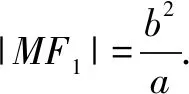

图5
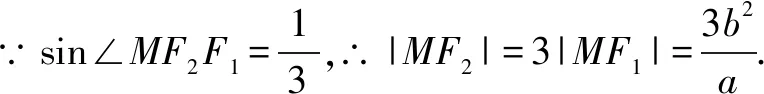

点评本题考查双曲线的定义及离心率的求解,关键是找出几何量之间的关系,考查数形结合思想,属于中档题.
例8(2015·新课标Ⅱ理11)已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,顶角为120°,则E的离心率为( ).


点评本题考查双曲线的方程和性质,主要考查双曲线的离心率的求法,运用任意角的三角函数的定义求得M的坐标是解题的关键.

分析利用已知条件,通过点A到渐近线的距离的两种不同表示式,列出关于a、b的方程,即可求出双曲线的离心率.


点评本题考查双曲线的简单性质的应用,点到直线的距离公式以及圆的方程的应用,考查转化思想以及计算能力.

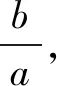
解答画出图形,由已知可得线段OA是△BF1F2的中位线,∴OA∥F2B.

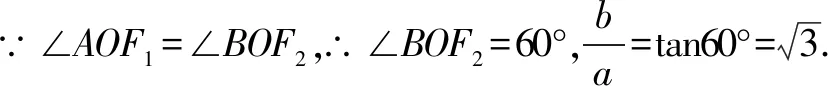
点评本题考查双曲线和平面几何的简单性质,考查数形结合的思想方法和计算能力,是中档题.
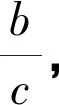
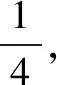
分析设出椭圆的方程,求出直线的方程,利用已知条件列出关于b、c的方程,即可求解椭圆的离心率.
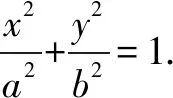

点评本题考查椭圆的简单性质的应用,点到直线的距离公式,椭圆的离心率的求法和计算能力.
四、列出关于a、b、c的方程,再结合a、b、c之间的平方关系,消去一个量,即可求出圆锥曲线的离心率.

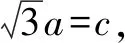

点评本题考查了双曲线的简单性质,点到直线的距离,余弦定理和离心率的求法,属于中档题.
可以看出,求圆锥曲线离心率的关键在于寻找相等关系,列出关于a、b、c的方程.常用的途径有:①借助已知的相等关系,如例1、例6和例11;②利用圆锥曲线的定义,如例2和例7;③根据“若点在曲线上,则点的坐标满足曲线的方程”,如例3和例8;④利用正、余弦定理,如例12;⑤根据图形的几何性质,如例4、例5、例9和例10.

