对一道高考模考题的解法探究和反思
2019-11-25 03:34李昌成
数理化解题研究 2019年31期
李昌成
(新疆乌鲁木齐市第八中学 830002)
一、题目


二、背景
本题作为二模的压轴题真正起到了把关作用.在我所教的两个班(共97名学生)中只有9人得分,得分率仅为0.093.全市得分率就更低(我校一本率在90%左右).因此,本题具有研究的价值,以便让学生把这类与圆内接四边形有关的数量积问题弄通透,让模考直通高考.
三、分析
本题以数量积作为背景,考查学生的综合运用知识的能力.而求数量积必须依靠相关长度和角度,因此解题要向这两个量靠拢.本题要依托三角函数、平面向量、平面几何、解析几何、正余弦定理等知识作为突破口进行分析解答,解题中等价转化尤为关键,抽丝剥茧,直到水落石出.
四、解答
1.以三角函数为突破口
解法1如图1,因为BD为圆的直径,所以∠BAD=∠BCD=90°.

由已知得∠ADB=∠ACB=∠ABC.

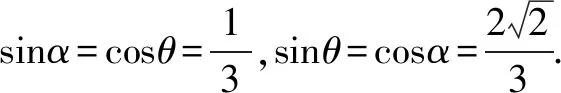
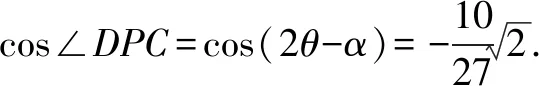
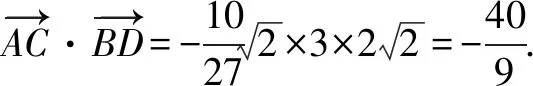
解法2 如图2,过点A作AE⊥BC,交BD于O,连结CO.
易得△AOB∽△AOC,所以∠BAO=∠CAO=∠ABO.
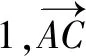
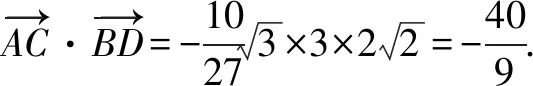
2.以平面向量为突破口
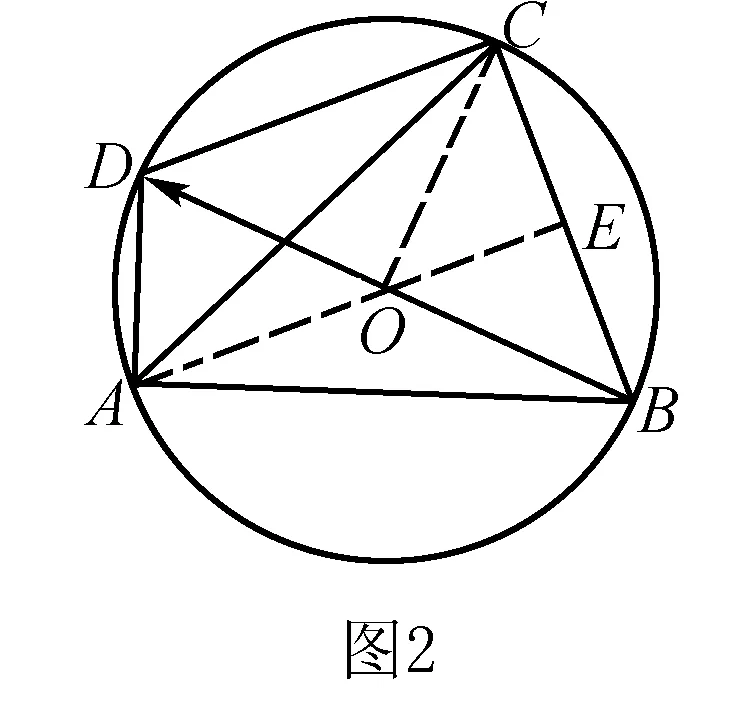
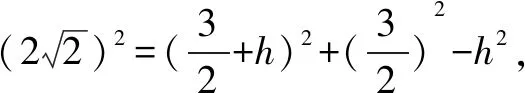
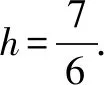
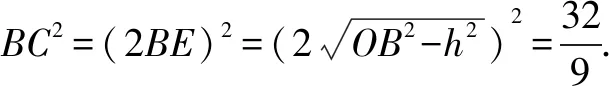

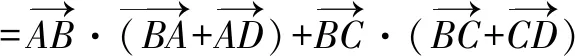

3.建立直角坐标系,以点C的坐标为突破口
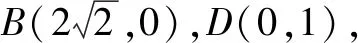

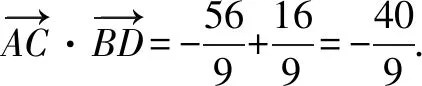
4.建立直角坐标系,依托正弦定理找到突破口
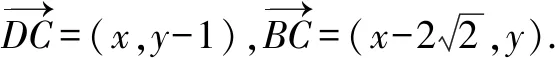

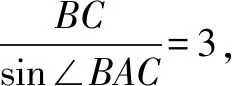
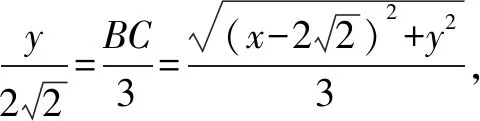
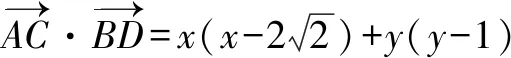
5.建立直角坐标系,依托余弦定理找到突破口
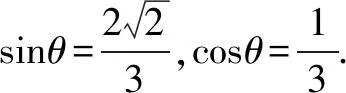
在△ABC中,AC2=AB2+BC2-2AB·BC·cosθ,
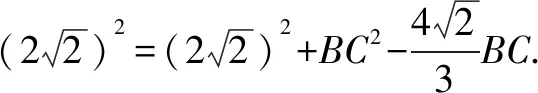

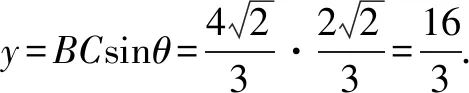
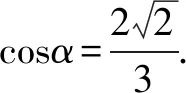

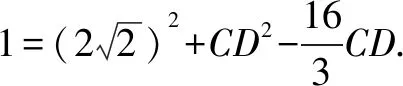

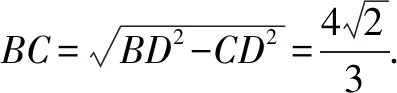
以下同解法7.
五、反思
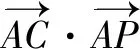
猜你喜欢
中学生数理化·七年级数学人教版(2022年4期)2022-04-26
中学生数理化·七年级数学人教版(2022年4期)2022-04-26
中学生数理化·七年级数学人教版(2021年4期)2021-07-22
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
河北理科教学研究(2020年1期)2020-07-24
华人时刊(2018年17期)2018-12-07
中学生数理化·七年级数学人教版(2018年4期)2018-06-28
高中生·天天向上(2018年2期)2018-04-14
智富时代(2017年4期)2017-04-27

