不惧计算 勇于转化——2019浙江高考21题解法剖析

朱海英 蒋时捷

(1.浙江省绍兴市柯桥区越崎中学 312000；2.浙江省绍兴市柯桥区柯桥中学 312000)

原题再现：如图，已知点F(1，0)为抛物线C:y2=2px(p>0)的焦点，过点F的直线交抛物线于A,B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧.记△AFG,△CQG的面积分别为S1,S2.

(1)求p的值及抛物线的准线方程；

该题得高分的学生不外乎两种情形：一种是运算变形功底非常扎实，不惧计算——选择求出点G和点Q的坐标，直接利用三角形底乘以高的面积公式表示出面积比，进而化简求最值.我们称之为直接法；另一种灵活果断，勇于转化——巧妙利用重心的性质把面积之比转化为线段之比，再进一步转化为坐标之比.我们称之为等价转化法.下面具体剖析这两种做法：

方法一 直接法

设直线AB的方程：x=ty+1(这里不妨设t>0，A在x轴的上方,这样可以避免绝对值带来的麻烦)与y2=4x联立得:y2-4ty-4=0,即得y1+y2=4t.

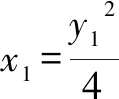
分子分母同除以t3得:

方法二、等价转化法

设直线AB的方程：x=ty+1(这里不妨设t>0，A在x轴的上方,这样可以避免绝对值带来的麻烦)与y2=4x联立得:y2-4ty-4=0,即得y1+y2=4t.

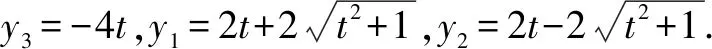
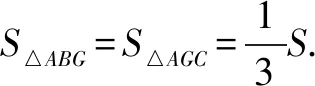
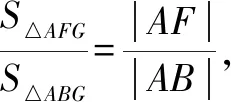
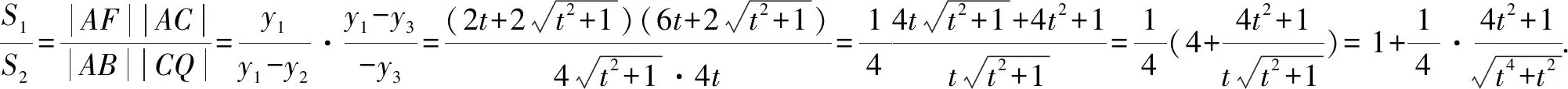
令m=4t2+1(m>1),

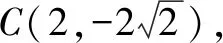
∴G(2,0)