基于GM(1，1)模型残差修正的经济预测

邢 晏，冯长焕

(西华师范大学数学与信息学院，四川南充637000)

灰色系统理论是一种研究少数据、贫信息不确定性问题的新方法，它以“部分信息已知、部分信息未知”的“小样本、贫信息”不确定性系统为研究对象，灰色系统是指白色系统和黑色系统之间的数据系统。［1－2］灰色系统理论将随机过程看作在一定范围内变化且与时间有关的灰色过程，将一切随机变量看作在一定范围内变化的灰色量，采用灰色生成方法，将杂乱无章的原始数据整理成较强规律性的生成数列再作研究。［3－8］灰色预测理论作为灰色系统理论的重要部分，同时也是一种新的现代预测方法。［9］此方法具有预测精度高、所需原始信息少且计算过程简单等优点，是一种对含有不确定因素的系统进行预测的方法，用生成模块建立微分方程模型，通过少量的、离散的数据寻找规律，时效性较强，比较适合“少数据建模”［10］。

近年来，普遍认为GM系列模型预测比较接近实际，目前已广泛应用于社会、经济、科技等各大领域。然而，由于灰色理论体系本身还不够完善，特别是GM(1，1)模型，作为灰色系统理论的核心，是基于解决实际问题而产生的，该模型仅适用于具有较强指数规律的序列，对于一些摆动较大的数据，预测误差往往较大，模型检验常常不能通过。由此，对传统GM(1，1)预测模型通过残差修正建立灰色残差模型进行优化，提高模型经济预测精度，具有一定的实际应用价值。

1 GM(1，1)模型的建立与检验

1．1 GM(1，1) 模型建立

设原始时间序列为X(0)，满足X(0)=(X(0)(1)，X(0)(2)，…，X(0)(n))，通过累加，即

生成新序列

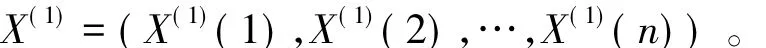
GM(1，1)模型相应的微分方程为

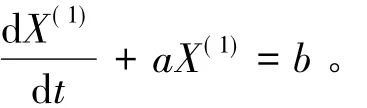
其中:a为发展系数，b为内生控制系数。

求解微分方程，得GM(1，1)预测模型

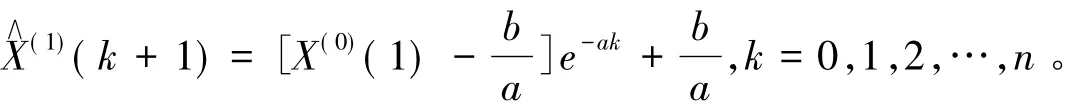
1．2 GM(1，1) 模型的检验

在GM(1，1)模型建立之后，一般要通过模型检验，检验包括残差检验、关联度检验及后验差检验等过程。

1．2．1 残差检验

由预测模型得到 X∧(1)(i) ，将其通过累减，即 X∧(1)(i)=X∧(0)(i) － X∧(0)(i － 1) 得到 X∧(0)(i) ，从而求出X(0)(i)与X∧(0)(i)的误差序列:

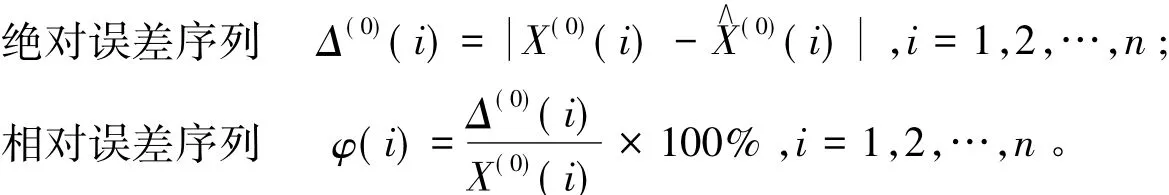
1．2．2 关联度检验

首先，根据关联系数的定义算出X∧(0)(i)序列与X(0)(i)序列的关联系数。

定义1 关联系数η(i)为

其中:

(1)令 Δ(0)(i)= X∧(0)(i) － X(0)(i)为第i个点X(0)与X∧(0)的绝对误差。

(2)minΔ(0)(i)为第一级最小差，minminΔ(0)(i)为第二级最小差。同理，maxΔ(0)(i)为第一级最大差，maxmaxΔ(0)(i)为第二级最大差。

(3)分辨率 ρ∈ (0，1) ，通常取 ρ=0．5。

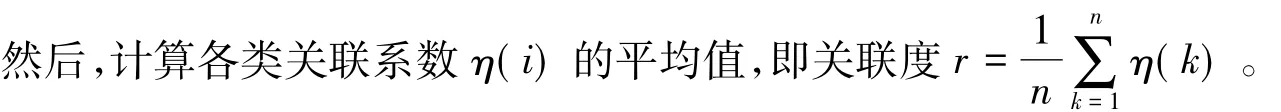
从实际经验出发，取ρ=0．5，当r＞0．6时达到满意程度。

1．2．3 后验差检验

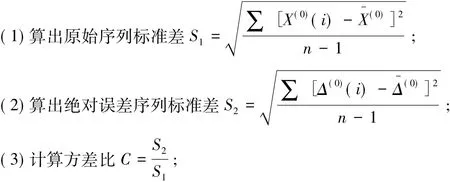
(4)计算小误差概率P=p{Δ(0)(i)－Δ－(0)＜ 0．674 5S1} 。

若令li= Δ(0)(i)－Δ－(0)，S0=0．674 5S1，则 P=p{li＜ S0} ，预测精度等级［11］见表 1。

表1 预测精度等级

若残差检验、关联度检验及后验差检验均能合格，则可以用GM(1，1)模型进行预测。否则，说明GM(1，1)模型检验不合格或精度不理想。为此，可对GM(1，1)模型进行残差修正，从而提高预测精度。

2 GM(1，1)残差模型修正

由原始序列X(0)建立的GM(1，1)模型

X(1)={X(1)(1)，X(1)(2)，…，X(1)(n)} ，得到预测序列

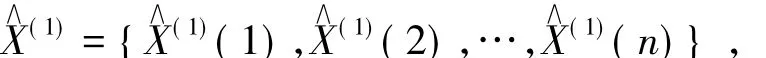
定义残差l(0)(j)=X(1)(j)－X∧(1)(j)，则与X(1)及X∧(1)对应的残差序列为

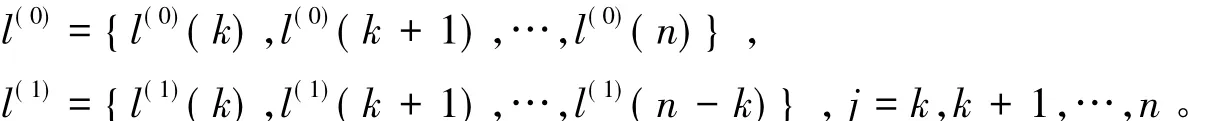
建立l(1)相应的GM(1，1)模型

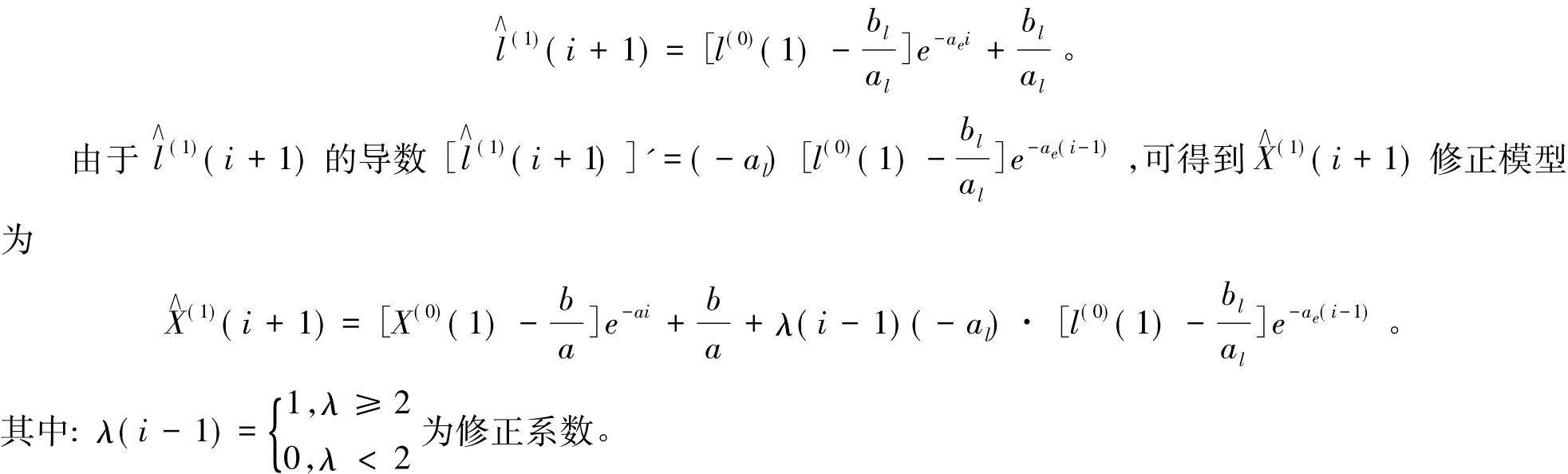
由此，得到经过残差修正的GM(1，1)原始序列预测模型

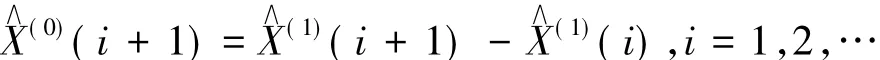
3 实证分析

表2为我国2012—2018年国内生产总值GDP总量资料。现根据资料建立GM(1，1)预测模型，分析今后短期发展趋势，可为相关政策的制定提供一定的参考。

表2 我国2012—2018年国内生产总值GDP总量情况(单位:万亿元)

3．1 模型建立

首先，令原始序列为

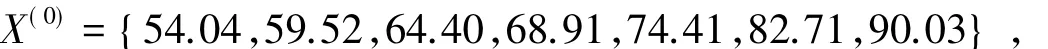
则累加生成序列

故 a=－ 0．083 863 06，b=51．837 434 9。

从而GM(1，1)预测模型微分方程为

3．2 模型检验

由原始序列平均值X－(0)=73．330，计算原始序列标准差为

并有

所有ek都小于S0，故P=1，C ＜ 0．35，后验差检验通过。

由GM(1，1)预测模型可知

可见，相对误差序列中有的相对误差较大，残差检验不通过。

对于关联度检验，min Δ(k)}{ =0，max Δ(k)}{ =0．72。

由于只有两个序列，故不再找第二级最差

可见，利用通常GM(1，1)模型检验不过关，下面进行模型残差修正。

3．3 模型残差修正

对上式求导，［∧l(1)(k+1)］'=0．536 7e0．0269k，得到经过残差修正后的 GM(1，1) 预测模型∧X(1)(k+1)=672．160 003e0．08386306k－ 618．120 003+ λ(k － 1)0．536 7e0．0269(k－1)。

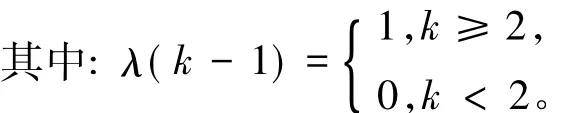
修正后，模型精度有较大提高，见表3。

综上可得，我国国内生产总值GDP总量预测值2021年为X(1)(10)－X(1)(9)=115．03万亿元。同理，2020年为105．78万亿元，2019年预测值为97．27万亿元。

可见，灰色残差修正的GM(1，1)模型预测精度较高，能够作为一种有效工具进行预测。

表3 GM(1，1)预测模型修正前、后的残差比较

用经过残差修正后的GM(1，1)模型来预测国内生产总值GDP总量:

当 k=7时，X(1)(8)=591．50(万亿元);

当 k=8时，X(1)(9)=697．28(万亿元);

当 k=9 时，X(1)(10)=812．31(万亿元)。

4 结论

普通灰色GM(1，1)模型仅描述服从指数变化的过程，预测精度较低，当检验不能通过可对灰色预测值进行残差修正，通过灰色残差模型预测精度明显提高，从而较好满足我国国内生产总值GDP总量的预测需要，为宏观经济政策的制定提供一定参考。由于灰色预测模型具有“小样本、贫信息”特点，只适合于短期预测。在实际运用中，要注意把握建模的时间序列参考元素，构造动态的灰色GM(1，1)残差模型，更好地提高模型的适用性与精确性。此外，由于数据选取、数据处理、修正对象和修正方法等因素不同，所建立残差模型的复杂程度、预测精度也有一定差别，而采用残差直接建模一次还原的算法，都具有复杂程度低、预测误差小等优点。