斐波那契行列式序列若干问题探究

吕淑婷

(北方民族大学数学与信息科学学院，银川750021)

0 引言

行列式序列应用于许多自然学科领域，作为线性代数的一个重要分支，目前已经取得很多成果。斐波那契行列式序列在邱森主编的《高等代数探究性课题精编》一书中就有研究，它是一个类似于斐波那契数列的行列式序列，有着类似的递推公式，斐波那契数列以如下被以递归的方法定义［1］:

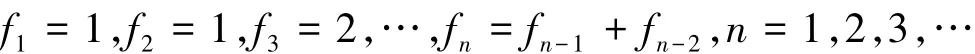
斐波那契行列式序列在给定一个三对角矩阵(主对角线元素为1，上对角线元素为－1，下对角线元素为1)以如下被以递归的方法定义:

在研究构造斐波那契行列式序列中，三对角行列式和海森堡行列式起着至关重要的作用。在线性代数、计算数学中三对角行列式的研究一直受到人们的关注，如三对角行列式的计算，用三对角行列式推导斐波那契数列的通项公式。同时，三对角行列式是海森堡行列式的特例，海森堡行列式在数值代数中有着重要作用，本文也介绍了海森堡行列式的定义以及在计算行列式方面的应用。

1 斐波那契行列式序列

斐波那契数列与斐波那契行列式序列之间的关系，简单来说就是行列式序列计算得到的数可以构成一个斐波那契数列。

例1［2］Fn是主对角线元素为2、上对角线元素为1、主对角线以下元素皆为1的矩阵

只要将|Fn|按照第1列展开就可以得到|Fn|=|Fn－1|+|Fn－2|，n≥3，从而构成斐波那契行列式序列。

定义1 行列式序列 {|Fn|} ，即 |F1|=2，|F2|=3，|F3|=5，|F4|=8，…，|Fn|=|Fn－1|+|Fn－2|，n≥3构成斐波那契行列式序列。

2 斐波那契行列式序列与三对角行列式

定义2 主对角线上的元素与主对角线上方和下方第一条次对角线上元素不全为0，而其余元素全为0的矩阵为三对角矩阵，形如

对于行列式|B|，我们称之为三对角行列式，有

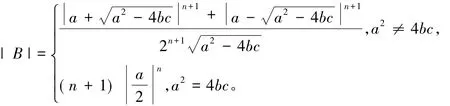
(1)用三对角行列式可推出斐波那契数列的递推公式Dn=Dn－1+Dn－2

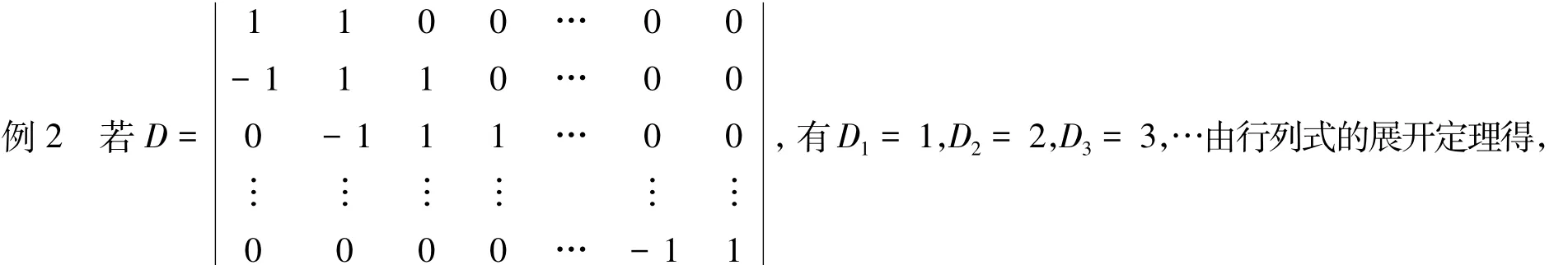
当n＞2时，Dn=Dn－1+Dn－2满足斐波那契数列的递推关系式及其初始条件。

(2)表示斐波那契数列的通项公式

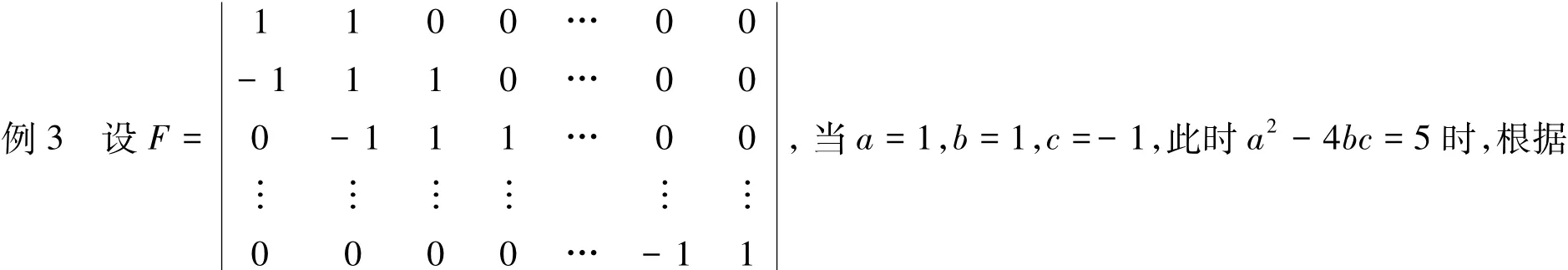
三对角行列式的计算公式，有a2≠4bc，由

可得斐波那契数列的通项公式［3－4］

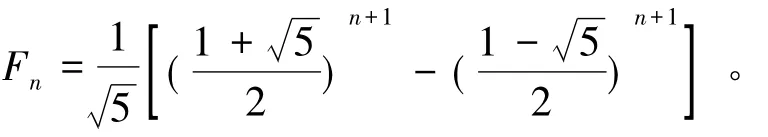
3 斐波那契行列式序列与海森堡行列式

定义3 对于方阵H，若i＞j+1时，元素aij为0，则称H是上海森堡行列式;若i＜j－1时，元素aij为0，则称H为下海森堡行列式，形如

为下海森堡行列式。

容易看出，上海森堡行列式的下对角线以下的元素全为0，而下海森堡行列式的上对角线以上的元素全为0。

而三对角行列式是海森堡行列式的特例，如果A既是上海森堡行列式，又是下海森堡行列式，则称A为三对角行列式，其非零元素只在三条对角线上出现，因而斐波那契行列式序列也可由海森堡行列式构造。

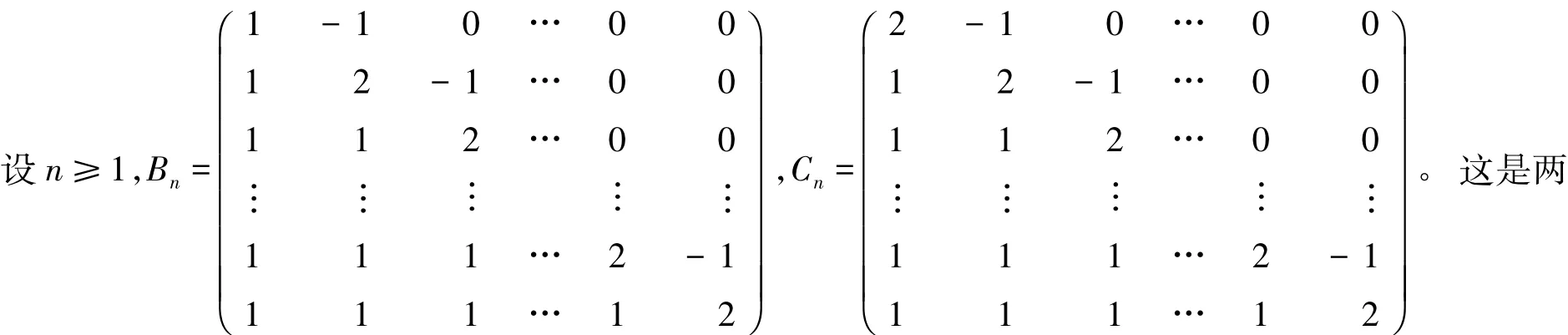
个n阶海森堡矩阵，而b11=1，c11=2，可得递推公式

因而行列式序列 B1、C1、B2、C2、B3、C3、B4、C4、…构成斐波那契行列式序列1、2、3、5、8、13、21、34、55、…

进一步，如果将Cn中的上对角线的元素都改为1，得到n阶海森堡矩阵

将 Fn按照第n列展开，得到 Fn= Fn－1+ Fn－2，n≥3，因而行列式数列 { Fn}构成斐波那契序列。

对于以上，得到的是特殊的海森堡矩阵的行列式构成斐波那契序列，下面将此结论加以推广，得到一般的海森堡矩阵行列式的递推公式。

命题1 设n阶海森堡矩阵

n≥1，定义 H0=1，H1=h11。

证明 ⅰ)当n=2时，H2=h22h11－h21h12，成立;

ⅱ)假设对n=k时，结论成立，则当n=k+1时，按第k+1行展开，有

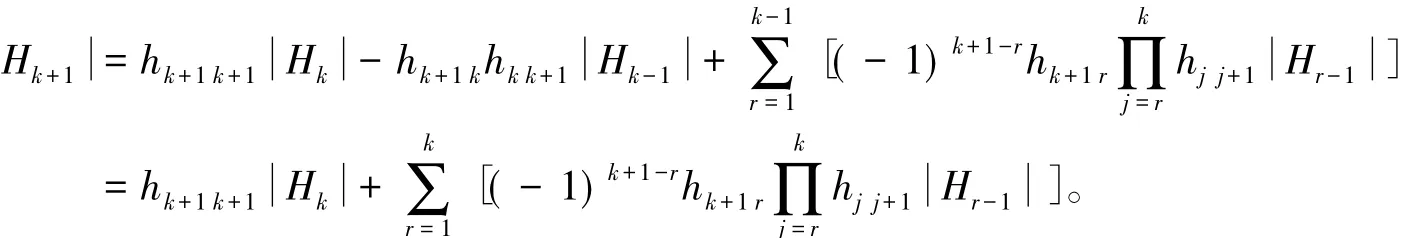
在实际中，很多行列式可以化归为三对角行列式、海森堡行列式，利用斐波那契递推公式或其他递推公式计算出行列式的值，而递推法对大多数海森堡行列式的计算都行之有效。

4 行列式计算的应用

(1)化为海森堡行列式去计算

例4 计算n阶行列式

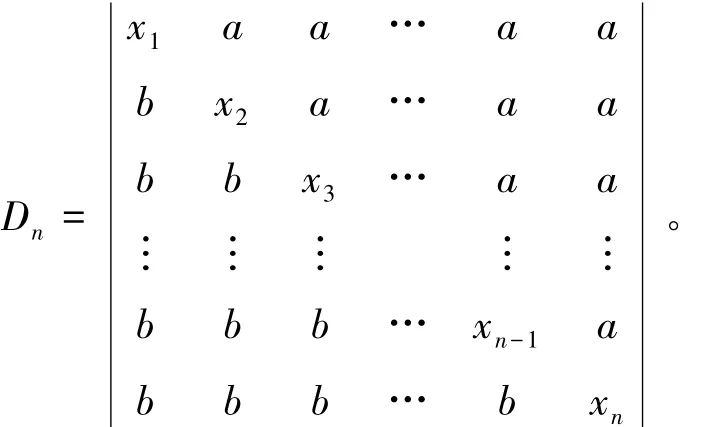
解 从最后一行开始，后一行减去前一行转化为海森堡型行列式

按最后一列展开，利用行列式性质有

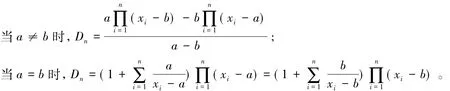
以上介绍了如何将一些行列式转化为海森堡型行列式，然后利用递推公式计算，需要注意的是在递推的时候也有一些技巧在里面，这也是上面这种方法在运用中的一个难点，转化为海森堡型行列式来计算的方法也许不是这些行列式最简单的计算方法，但不失为一种启发思维的好方法。

(2)利用三对角行列式［5－6］这是一个行列式值符合广义斐波那契序列的情况=0(p2+4q＞0)的两根，满足Dn=pDn－1+qDn－2，当p=q=1时为斐波那契序列，此时方程x2－px－q=0就为x2－x－1=0的两根，分别为，同样可求得Dn的通项为

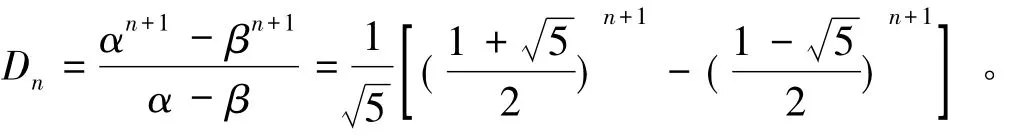
当然，用上面的结论易得

这为求一些特殊的行列式提供了方法。