相对论性多普勒效应研究

潘营利

(渭南师范学院物理与电气工程学院，陕西渭南714099)

0 引言

多普勒效应是一个非常重要的物理现象，在实际当中有许多重要的应用，因此在物理学教材［1－3］中，都要研究这一重要的物理现象。但教材中研究的都是低速情况下的多普勒效应，没有考虑其相对论效应。高炳坤、王凤林［4］给出了相对论性多普勒效应的简易推导;彭学杰［5］指出光波多普勒效应实际上是声波多普勒效应下的光学极限，光波多普勒效应只是波源和观察者相对速度的函数，表明光在真空中传播时媒介物是多余的;黄兴滨［6］给出了一个推导长度收缩和纵向多普勒效应的新方法，该方法可更直观理解在两个惯性系中观测一个纵向光波的波长与观测沿纵向静止于某个系中杆的长度的本质区别;Nizar Hamdan［7］从洛伦兹力和相对论出发推导了相对论性多普勒效应公式，给出了关系式:c=λf=λ0f0。

以上这些研究方法要么比较烦琐，要么不够全面，本文给出了推导相对论性多普勒效应的一种简单方法，同时从光子图像和相对论的四维协变量出发推导出相对论性多普勒效应公式。结果表明，在研究相对论性多普勒效应时，光子观点和波动观点可以给出完全相同的结果，从而进一步证实了光的波粒二象性。

1 非相对论性多普勒效应

1．1 波源静止而观察者运动

先分析静止点波源的振动在均匀各向同性介质中传播的情况，如图1所示，O点表示点波源，同心圆表示波面，图中任意波面上波点的相位与相邻同心圆上各点的相位差都是2π，所以两相邻同心圆半径之差是波长λ0。设波相对于静止介质以波速v0传播，以f0表示波源振动的频率，则波长λ0、波速v0和频率f0之间的关系为

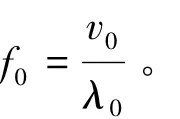
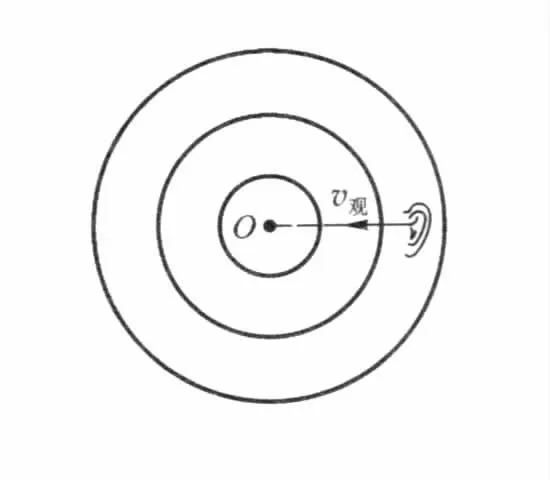
图1 波源静止而观测者运动时的多普勒效应

观察者观测到的波速v与观测到的波长λ之比称为观测频率，记作f，即

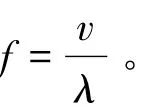
显然，若波源和观察者都相对于介质静止，则f=f0。

如果观察者相对于介质以速率度u朝波源O运动。由于经典力学不考虑相对论效应，即从不同参考系测量同一物体的长度是相同的，所以，尽管观察者以u运动，他测量上述球面波的波长λ仍等于λ0，但是观察者相对介质以速率u朝波源运动，所以他观测到的波速应为v0+u。观测频率f应为

同理，若观察者以速度u远离波源运动，则有

1．2 观察者静止而波源运动

假定点波源的振动在均匀各向同性介质中传播，如图2所示，设t=0时点波源在O点静止不动，波在介质中的传播速度为v0，一个周期T后波传到S处，其波长为λ0=v0T，波的频率为

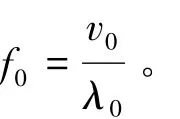
现假定波源以速度v向观察者运动，这样一个周期后波源运动到O'点，但波仍然传到S点，由于观察者相对于介质静止不动，波的传播速度仍然是v0，但波长变为λ，由图2知

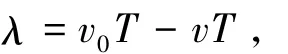
所以

可见频率变大了，对于声波，相当于声调变高。

如果波源以速度v远离观察者运动，同理可得

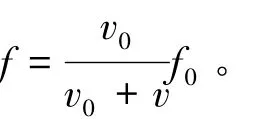
1．3 观察者和波源在同一直线上同时运动

现假定波源相对于介质以速度v向观察者运动，观察者相对于介质以速度u向波源运动，此时波速为v0+u，而波长为λ=v0T－vT，故观察者观测到的波的频率为

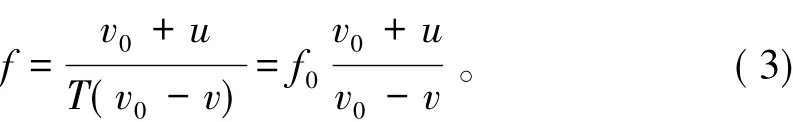
2 相对论性多普勒效应公式的推证

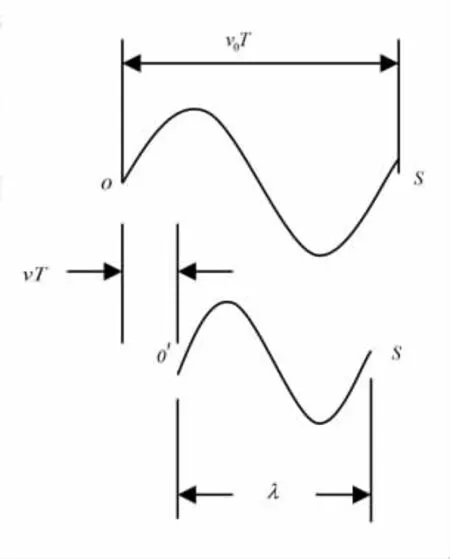
图2 波源运动时的多普勒效应

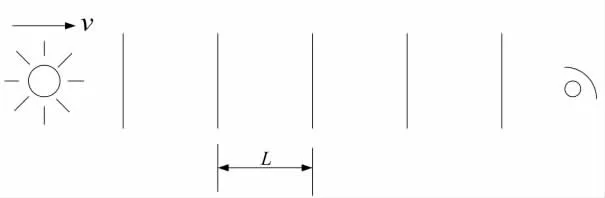
图3 光源以速度v向着观察者运动

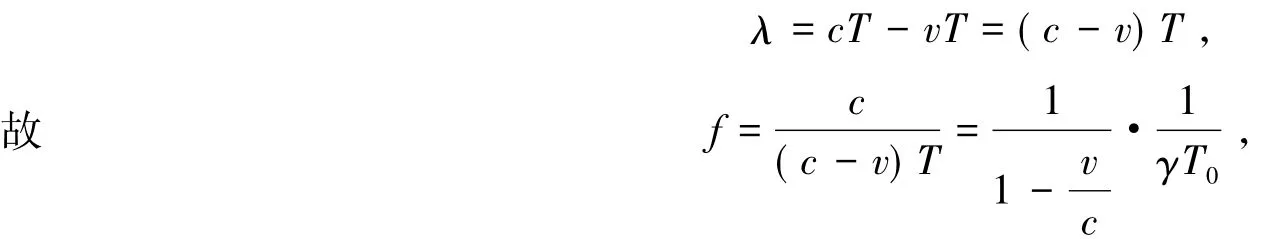
化简，得

其中:f是在观察者静止的坐标系中的频率，而v是光源和观察者的相对速度。式(5)中没有涉及相对于媒质的运动，可以看出相对论性结果不支持两个经典结果中的任何一个，它和二者都不相符。

3 观察者不在运动方向上的多普勒效应

下面研究观察者不在运动方向上的相对论性多普勒效应。光源静止时，发射光的频率为f0，周期为T0，如图4所示。当光源以速度v运动时，其发射光的频率为f，周期为T，如图5所示。

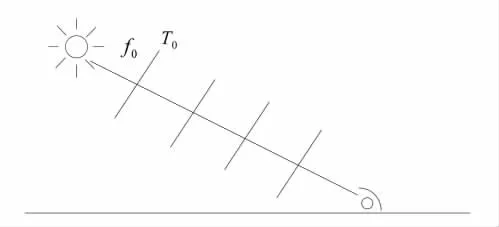
图4 相对于观察者静止的光源的发光情况

图5 光源以速度v沿水平方向运动

由图5可知 λ =cT－vT cosθ=(c－v cosθ)T，

其中:θ是在观察者静止的坐标系中测得的角度。若观察者在运动方向上，则θ=0，结果与式(5)相同;当这个“横向”多普勒效应是由于时间膨胀所引起的。

4 多普勒效应的光子图像

多普勒效应不仅可以从波动观点研究，也可从光子观点进行研究。考虑一个静止质量为M0的重原子，它处于稳定态。如果它发射一个能量为hf0的光子，则它的静止质量由M'0c2=M0c2－hf0给定。

现假设原子在发射光子之前以速度v自由运动，如图6所示，原子的能量为。在发射一能量为hf的光子后，原子的速度为u，静止质量为M″0，能量为E'，动量为P'。

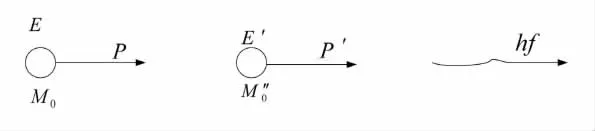
图6 运动原子发射光子

为简单，假定光子是沿运动方向发射的，由能量和动量守恒定律得

按照能量－动量关系得

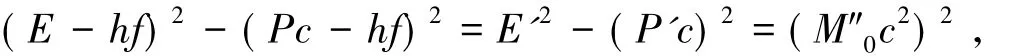
将左边展开，并采用E2－(Pc)2=(M0c2)2，考虑到是重原子，令M'0≈M″0，则得

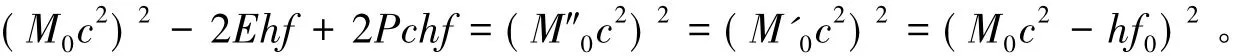
将其化简后得

结果与式(5)相同。可见用光的两种完全不同的观点(波动观点和粒子观点)对多普勒效应描述的结果相同。

5 四维协变量与多普勒效应

下面从相对论的四维协变量出发，推导相对论性多普勒效应公式。

设想有一x'y'坐标系，该坐标系以速度v相对于xy系在x方向运动，如图8所示，在x'y'系中，动量－能量四维协变量为

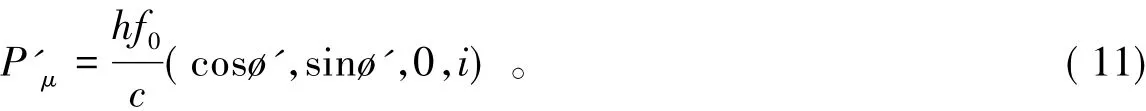
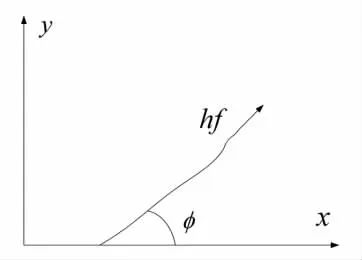
图7 在静止坐标系观察光子的频率为f

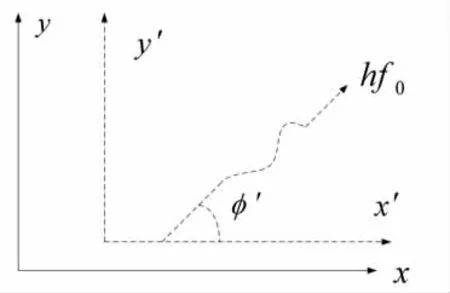
图8 在运动坐标系观察光子的频率为f0

由相对论知，一个四维协变量 Aμ=(A1，A2，A3，A4)的变换法则为

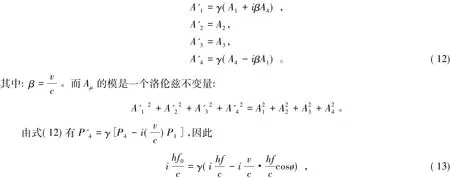
整理得

结果与式(6)相同。

6 结论

本文通过研究得出以下结论:

(1)给出了推导相对论性多普勒效应公式的一种简便方法;

(2)从光子图像出发，推导出了相对论性多普勒效应公式;

(3)从相对论的四维协变量出发，推导出了相对论性多普勒效应公式;

(4)研究结果表明，在研究相对论性多普勒效应时，光子观点和波动观点可以给出相同的结果，从而进一步证实了光的波粒二象性。