几何画板优化中学数学教学刍议

◎ 魏继善 姚素敏 杨 柯

随着新课改的不断深入，数学学科教学改革的紧迫性日益凸显，《新课程标准》中明确要求，初中数学要培养学生数形结合能力，能够具有独立的数学思想处理数学问题。几何画板的出现与应用，极大地推动了数学课堂转型，帮助学生快速树立数形结合思想，通过实际操作成为数学课堂的主人，高效掌握数学知识。

一、几何画板概念界定

几何画板，是基于当前新媒体发展下的新教学技术，是适用于数学平面几何、函数，物理矢量图作图的动态几何工具，该教育软件可以帮助教师创造性地实现课堂教学内容。

传统的数学课堂中，教师利用圆规与直尺，在黑板上绘制教学内容中所需的几何图形，尺规作图，成为一个时代数学教学的传承方式。但这种方式具有局限性，例如课堂时间有限，绘制标准图形进行演示需要耗费时间。同时，平面静态的图形，不能够很好地给予学生直观感受，不利于学生数学思维的形成，这与当前新课改下数学教学意义相悖。

几何画板的出现，更侧重于动态几何图形的构建，操作几何图形“点”“线”“圆”的元素，保持几何关系不变，对元素轨迹进行探寻，让学生及时了解几何原理，课堂高效完成。同时，软件技术能够让图形计算、演示科学化，让动态演示结果及时反馈在屏幕中，交互性强的同时做到精准无误。

二、几何画板的特点与优势

1.动静结合，功能性强。中学数学不同于小学数学，其难度体现在思维方式与逻辑变换中。代数与几何的出现，让数学学习更具抽象性，更要求中学生能够建立起数学思维，解决数学难题。几何画板，为数学课堂提供了另一种可能性，即利用其软件特性，将数学课堂“活”起来。在课堂中，点击鼠标对立体几何的元素(点、线、圆)进行拖动等操作，实现不同条件下的教学任务。如讲到“三角形”这一课程，教师演示拖动三角形三边，便可在动态变换中，形成不同形状的三角形，找到几何规律。

2.立足教学，灵动性强。中学数学教学具有抽象性特点。教师在教授过程中，利用几何画板，可以随时根据教学内容的推进，将重点体现在画面中，几何画板成为“动态黑板”，让枯燥的数学内容灵动起来，也让教学效率提升。

3.简单易学，实操性强。几何画板基于计算机技术，简单操作易上手，符合当前学生对于学习的兴趣基点，依靠工具栏和菜单，就能让教师以最简单的操作实现抽象化的问题，实现中学数学中重要的“几何关系变化”教学内容，也能让学生实际操作，增强课堂互动性，在实操中加深学习印象。

三、几何画板优化中学数学教学实践

几何画板有诸多应用优势，为中学数学教育带来丰富发展空间，对于立体几何等教学内容提供了很大帮助，让学生在学习过程中提升自身数学能力。我们应当更好地将其应用于数学教学实践中，同时要注意遵循相应的原则，为课堂实践奠定基础。

1.课堂角色的转变。几何画板的出现，是新课改要求下数学教学模式转变的载体，其目的是为了让学生更好地学习数学，培养其思维能力和数学素养。因此，几何画板并不意味着教师掌控话语权，而唯有学生成为课堂的实践主题，真正参与到利用几何画板载体进行的教学活动中。

2.尊重差异性。将几何画板应用于中学数学课堂中，教师应当因材施教，根据不同学生理解、接受程度，巧妙运用几何画板易操作功能特性，帮助学生通过自身努力与实际操作获取知识，既保证教学又兼顾实操，给予不同层次学生不同的学习、观察空间，尊重学生之间的差异性。

3.平衡适度原则。几何画板最大的优势，是能够动态展示数学元素变化过程，增添学生理解的直观性。但同时，这种直观性也会让学生依赖形象思维而忽视抽象的逻辑思维，这与数学教学目标相悖。而学生在解决实际问题时，也没办法随时运用几何画板建模操作。因此，教师应当注意运用时达到直观与抽象的教学平衡。

四、课堂环境的创设

几何画板引入课堂，学生动手操作机会增多。这部分时间内的教学，应当更加科学化，通过互动性、开放性的课堂环境，教师引导学生自主解决问题，培养学生之间的合作意识格外重要。但也应注意，决不能因过分追求教学新鲜，而本末倒置忽略了教授知识的本原目的。

中学数学，其难度的增加也让教学任务难度升级，如何培养学生数形结合思想，让学生更好地解决不断升级的难题，成为中学数学教师的主要任务。因此，利用好几何画板这一工具，重新探析数学问题，成为突破思路，可以由浅入深，将这种工具优势不断渗透至教学的各个阶段，完成其应有的功效。

1.以兴趣奠基，促习惯养成

以兴趣为驱动力，是数学学习的基础，也是为今后数学能力、思维的培养奠基。因此，可从七年级开始，在课堂中运用几何画板，让学生对于几何画板教学有初步认识，学习其简单的基本操作。例如，七年级数学(人教版)第四章第一节《多姿多彩的图形》，教师可从直线和线段等基础概念入手，引导学生进行操作，以实际授课内容让学生了解几何画板的菜单功能，并在操作中及时纠正学生错误，形成良好互动。学生在初入中学数学课堂时，对几何画板有初步了解，形成使用习惯，让其能够成为日后数学学习的好帮手。

2.以操作突破，转课堂角色

几何画板的动态直观性功能，是学生需要充分利用的学习点。因此，八年级几何知识难度升级，对于一些抽象性极强、不易被理解的知识内容，可以通过实际操作几何画板，让学生从自主探究中掌握知识，身历其境感受运用几何画板解决数学问题的情境，切实转变课堂角色，让学生成为课堂学习的主人。

八年级数学第十一章，研究全等三角形与角的平分线。此章节从三角形的相关知识入手，利用对形的认识，解决实际生活中的实际问题，具有极强的现实意义。因此，教师在课堂中应让学生自主操作，在几何画板中，指导学生画出任意三角形角的平分线、中线、高，让学生感受这三条线原来是不重合的，然后再以特殊三角形——等腰三角形的三线，发现三线合一的规律，在两种情形下，学生通过自主操作，积极形成对图形认识的推断与思维逻辑，对于该章节内容理解更为透彻。

3.以问题导向，使能力形成

几何画板地引入，其目的最终是为了让学生能够养成数学逻辑思维与正确的解题思路，从而更好地形成数学应用能力。因此，数学课堂中，应当以更为开放的问题导向为教育环境，以问题促实践，最终帮助学生养成利用几何画板构筑正确数形结合思维的能力，去解决难题。

九年级这一阶段，学生面临升学考试，且数学问题难度升级，发现问题且能够自主构建模型解决，是九年级学生应当具备的素质之一。

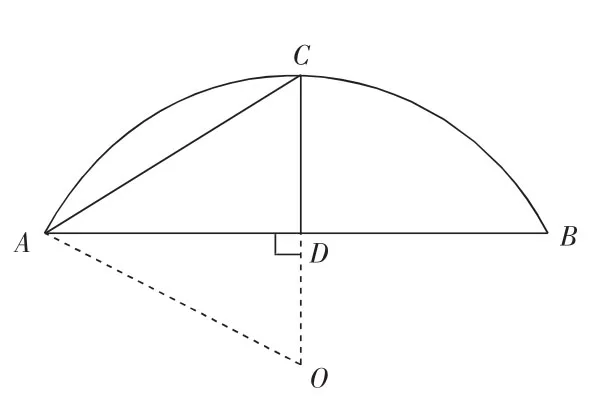
如，实际生活问题的情境创设。

如图所示，现要建造一蔬菜大棚，为保证效果，根据土地面积，需要将大棚设计为拱门宽度8米，拱门弧度为30°左右，那么大棚需要建造多高，才能保证大棚顺利建造？

学生应当将实际图形转化为数学模型，在自主构建的数学模型中完成解答：

AB代表大棚宽度，∠CAD为拱门弧度，问题所求为CD长度。因此，题被转换成简单的数学算数，利用三角函数公式，可求得大棚的高度CD约为2.3米。

几何画板的动态功能性，已被课堂广泛应用。作为辅助教学的工具，丰富课堂的同时，还迅速让学生将数学问题转化为已知的数学知识，激发其创新精神。同时，几何画板也是一把双刃剑，舍本逐末的表面功夫也成为课堂“杀手”，应当加以防范，让几何画板切实落实于数学原理教学。完善几何画板教学，我们任重道远，笔者相信会有更多成果，此举势在必行。