黏接界面脱黏的亚谐波共振识别方法

刘俊毅，肖 黎，屈文忠

(武汉大学 工程力学系，武汉 430072)

黏接构件广泛应用于现代工业领域,黏接界面脱黏是导致结构完整性破坏的主要原因之一，对黏接界面进行有效的检测和评估其黏接质量具有重要的意义[1]。

近年来，非线性超声方法[2]广泛运用于结构的损伤识别研究中，国内外学者运用非线性超声方法对黏接结构的检测做了大量的研究。安志武等[3]建立了黏接界面横波和纵波的非线性弹簧模型，验证了二次谐波等非线性参量对黏接界面厚度变化较为敏感。江念等[4]以二次谐波幅值与反射基波幅值平方之比表征黏接界面超声非线性程度,并作为有效评价复合结构黏接质量的特征参数。Achenbach等[5]指出黏接失效是黏接界面处的非线性行为导致的，黏接界面处的非线性行为会导致高次谐波的出现。Yelve等[6-7]研究发现从高次谐波提取的损伤指数能有效识别加筋铝板的脱黏以及压电传感器与基底间的脱黏损伤。Shui等[8]利用非线性超声方法对黏接接头疲劳损伤进行了研究，并探讨了二次谐波产生的原因。上述研究均是利用高次谐波检测结构黏接质量，但高次谐波信号容易受到传感器、功率放大器等测试设备引起非线性因素的影响，这些成分作为背景噪声掩盖了损伤信号，降低了信噪比，因此以高次谐波成分表征黏结界面处的非线性特征容易受到背景噪声的干扰，从而产生损伤误报。而非线性超声的亚谐波成分只有在固体界面处的冲击碰撞与振动接触时并在特定激励条件下才能产生，与测试环节无关，使得亚谐波更适合于黏接界面脱黏的识别研究。在利用亚谐波进行损伤检测方面，Ohara等[9]利用亚谐波阵列方法检测闭合裂纹的深度。Guédra等[10]研究了均匀单分散气泡云的亚谐波阈值。Singh等[11]对复合材料分层损伤进行了有限元模拟分析，研究结果表明分层引起结构的非线性行为会导致超谐波和亚谐波成分产生。Zhang等[12]利用亚谐波共振方法对非线性边界条件下疲劳裂纹进行了损伤识别的研究。Maruyama等[13]建立并求解裂纹二维弹性波散射的边界积分方程，探讨了亚谐波产生的机制。

迄今为止，鲜有研究利用亚谐波共振的方法识别黏接界面的脱黏。本文提出一种基于亚谐波共振分析的黏接界面脱黏识别方法，以铝板黏接的梁结构为实验对象，进行黏接界面脱黏亚谐波共振的识别实验研究，结果验证了亚谐波共振方法识别界面脱黏的适用性和有效性。

1 理论分析

1.1 黏接界面定性模型

黏接构件在循环加载作用下，会导致黏接界面的破坏，黏接界面处界面间的力学性能发生改变，结构的刚度发生变化。为研究黏接界面脱黏时的超声非线性特征，以更好地表征黏接界面处的力学行为，本文将黏接界面简化为弹簧表征的非线性刚度模型，如图1所示。黏接界面由脱黏区和完好区组成，虚线表示黏接界面脱黏区，实线表示黏接界面完好区，如图1(a)所示。将黏接界面简化为图1(b)所示的单自由度非线性刚度模型，黏接界面完好区界面间呈线性刚度，用k表示。黏接界面脱黏区，由于黏接界面损伤导致界面刚度呈现非线性特征，界面间作用力与位移的关系用非线性弹簧Fc(x)表示。当无动态载荷作用时，界面1和界面2之间界面间作用力为零。界面1作用幅值为F频率为ω持续激励时，运动方程可表示为

(a)

(b)图1 黏接界面脱黏模型Fig.1 Interface debonding model

(1)

式中:m为质量，c为阻尼，k0为刚度；Fc为界面间作用力。

黏接界面脱黏引起黏接界面的非线性特征使界面间应力应变的关系不再符合经典线性胡克定律，需要引入更高阶的弹性关系[14]。本文根据脱黏界面的力学特征，引入最高阶为三次的多项式近似模拟黏接界面力与位移的关系，并定义黏接界面彻底失效的临界位移，定性给出界面间作用力Fc随界面1的位移x的关系，如图2所示。横坐标为界面1的位移x，纵坐标为界面间作用力，o为原点，a为黏接界面彻底失效的临界位移。当界面1的位移x小于0，界面间作用力表现为斥力并随着位移x数值的增大而增大，此时黏接界面受到挤压。当界面1的位移x大于0，界面间作用力表现为拉力并随着位移x的增大而增大，增大到最大值后，界面间作用力随着位移x的增大而减小，当界面1的位移x等于a时，界面间作用力变为0。当界面1的位移x大于a时，黏接界面失效，界面间作用力为0。界面力与界面1的位移x关系用式(2)表示。

(2)

式中，k1为非线性刚度，a为系数。

图2 界面力-界面1位移图Fig.2 Relationship between interface force and the displacement of interface 1

1.2 亚谐波共振分析

(3)

利用多尺度法[15]对式(3)求解，设一次近似解

x(t,ε)=x0(T0,T1)+εx1(T0,T1)

(4)

式中：T0=t，T1=εt。

将式(4)代入式(3)，分别令ε0，ε1的系数相等，得到

(5)

(6)

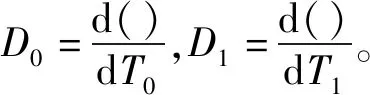
式(5)的通解为

x0=A(T1)cos[ω0T0+φ(T1)]+Bcos(ωT0)

(7)

将式(7)代入到式(6)得到

(8)

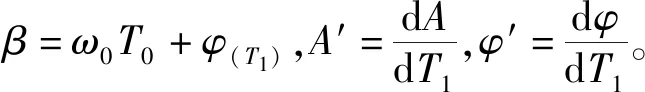
1.3 模型计算结果

为验证亚谐波产生机理，利用MATLAB对上述单自由度非线性模型进行求解。本仿真模拟黏接界面脱黏时，着重探讨非线性系统强迫振动过程中亚谐波共振的激励条件，而不考虑黏接界面材料、黏接界面脱黏区微观损伤形式等对理论模型参数选取的影响。式(1)中参数定性取为m=1，c=0.04,k0=0.1,k1=0.1，a=1。采样频率10 Hz，计算时长2 000 s。由于脱黏时黏接界面非线性特性对系统刚度的影响，导致系统的固有频率不能由质量与刚度直接计算得出，对该模型进行扫频激励，得到其线性系统的固有频率为0.070 5 Hz,如图3所示。

图3 扫频激励图Fig.3 The response signal with sweep excitation

由理论分析可知，对于平方和立方非线性振动系统激励频率取接近两倍或者三倍固有频率，将产生亚谐波共振。分别取激励频率ω为三倍固有频率0.211 5 Hz，激励幅值F为0.5以及激励频率ω为两倍固有频率0.141 Hz，激励幅值F为0.1，得到图4和图5所示的时域和频域信号图。

(a)时域信号

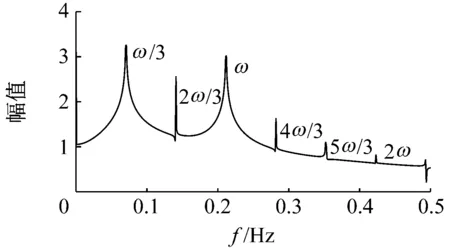
(b)频域信号图4 激励频率0.211 5 Hz，激励幅值0.5的响应信号Fig.4 The response signal with excitation frequency 0.211 5 Hz and excitation amplitude 0.5

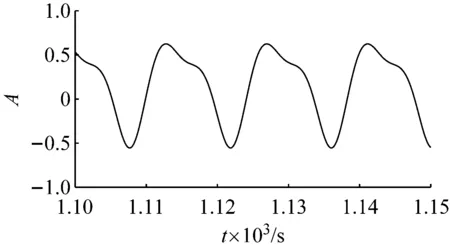
(a)时域信号

(b)频域信号图5 激励频率为0.141 Hz，激励幅值为0.1的响应信号Fig.5 The response signal with excitation frequency 0.141 Hz and excitation amplitude 0.1

由图4(a)和图5(a)可以看出，两者时域信号波形均出现明显扭曲，图4(b)频域信号中不仅出现了两倍激励频率(0.423 Hz)的超谐波信号，而且明显出现了1/3激励频率(0.070 5 Hz)、2/3激励频率(0.141 Hz)的亚谐波以及4/3激励频率(0.282 Hz)、5/3激励频率(0.352 5 Hz)的超亚谐波成分。图5(b)频域信号中不仅出现了两倍激励频率(0.282 Hz)的超谐波信号，而且明显出现了1/2激励频率(0.070 5 Hz)亚谐波以及3/2激励频率(0.211 5 Hz)超亚谐波成分。

任取远离两倍和三倍激励频率ω为0.18 Hz，激励幅值(0.5)与图4所取激励幅值相同，以及任取远离两倍和三倍激励频率ω为0.1 Hz，激励幅值(0.1)与图5所取激励幅值相同，分别得到图6和图7所示的响应信号的时域和频域信号图。

由图6和图7可以看出，两者时域信号图波形呈正弦，两者频域信号图中均只出现了两倍激励频率(0.36 Hz)和(0.2 Hz)的超谐波成分。

分别取激励频率ω为三倍固有频率0.211 5 Hz，激励幅值F为0.3，小于图4所取的激励幅值(0.5)以及激励频率ω为两倍固有频率0.141 Hz，激励幅值F为0.02，小于图5所取激励幅值(0.1)得到图8和图9所示的时域和频域信号图。由图8和图9可以看出，两者时域信号图波形呈正弦，两者频域信号图中均只出现了两倍激励频率(图8为0.423 Hz、图9为0.282 Hz)的超谐波成分。

对比图4和图6以及对比图5和图7可知，相同激励幅值条件下，图4和图6两种不同激励频率下频域中均出现谐波成分。与图6不同，图4中出现了亚谐波频率成分。图5和图7对比结果和图4与图6对比结果相似，图5和图7两种不同激励频率在相同激励幅值条件下结果中均出现谐波成分，与图7不同，图5明显出现了亚谐波频率成分。上述四图的响应信号频谱图中均出现超谐波成分，说明系统呈现非线性特征。而当激励频率为三倍固有频率或者两倍固有频率时将产生亚谐波，而远离两倍和三倍固有频率时响应信号中只有超谐波成分，据此得出亚谐波共振产生条件之一为激励频率接近三倍或者两倍固有频率。根据理论分析知，图4和图5中产生亚谐波成分是式(1)中非线性界面力项即黏接界面脱黏造成的。故利用亚谐波共振方法理论上能够识别黏接界面脱黏。

(a)时域信号

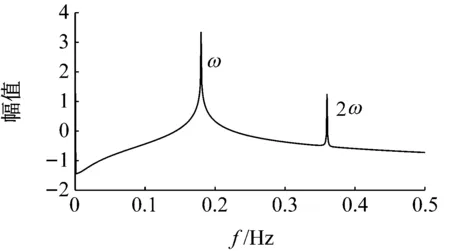
(b)频域信号图6 激励频率为0.18 Hz，激励幅值为0.5的响应信号Fig.6 The response signal with excitation frequency 0.18 Hz and excitation amplitude 0.5

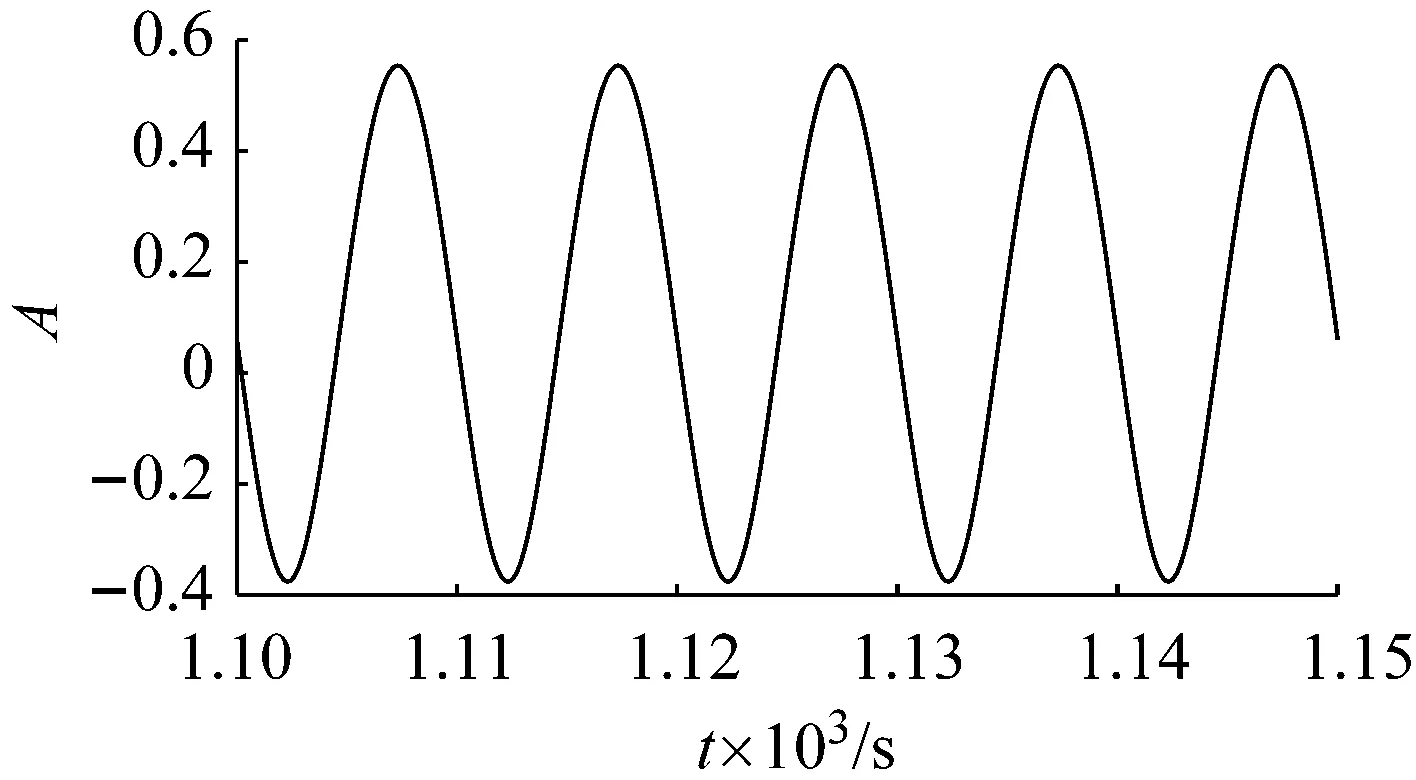
(a)时域信号

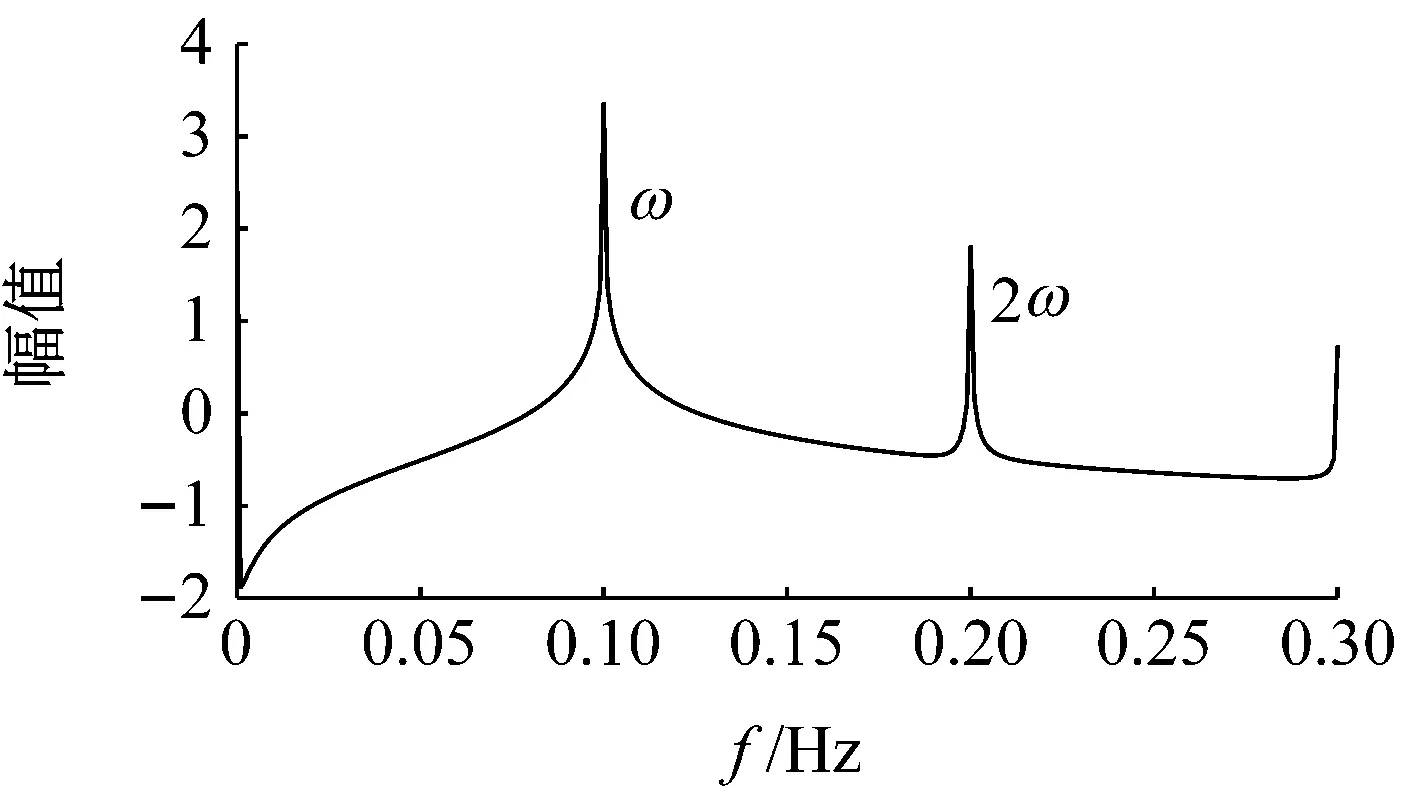
(b)频域信号图7 激励频率为0.1 Hz，激励幅值为0.1的响应信号时域图和频域图Fig.7 The response signal with excitation frequency 0.1 Hz and excitation amplitude 0.1

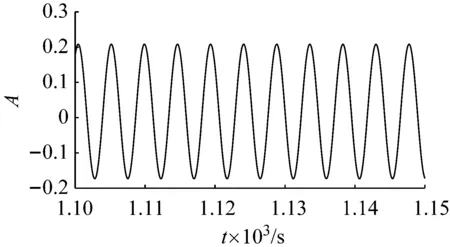
(a)时域信号

(b)频域信号图8 激励频率为0.211 5 Hz，激励幅值为0.3的响应信号Fig.8 The response signal with excitation frequency 0.211 5 Hz and excitation amplitude 0.3

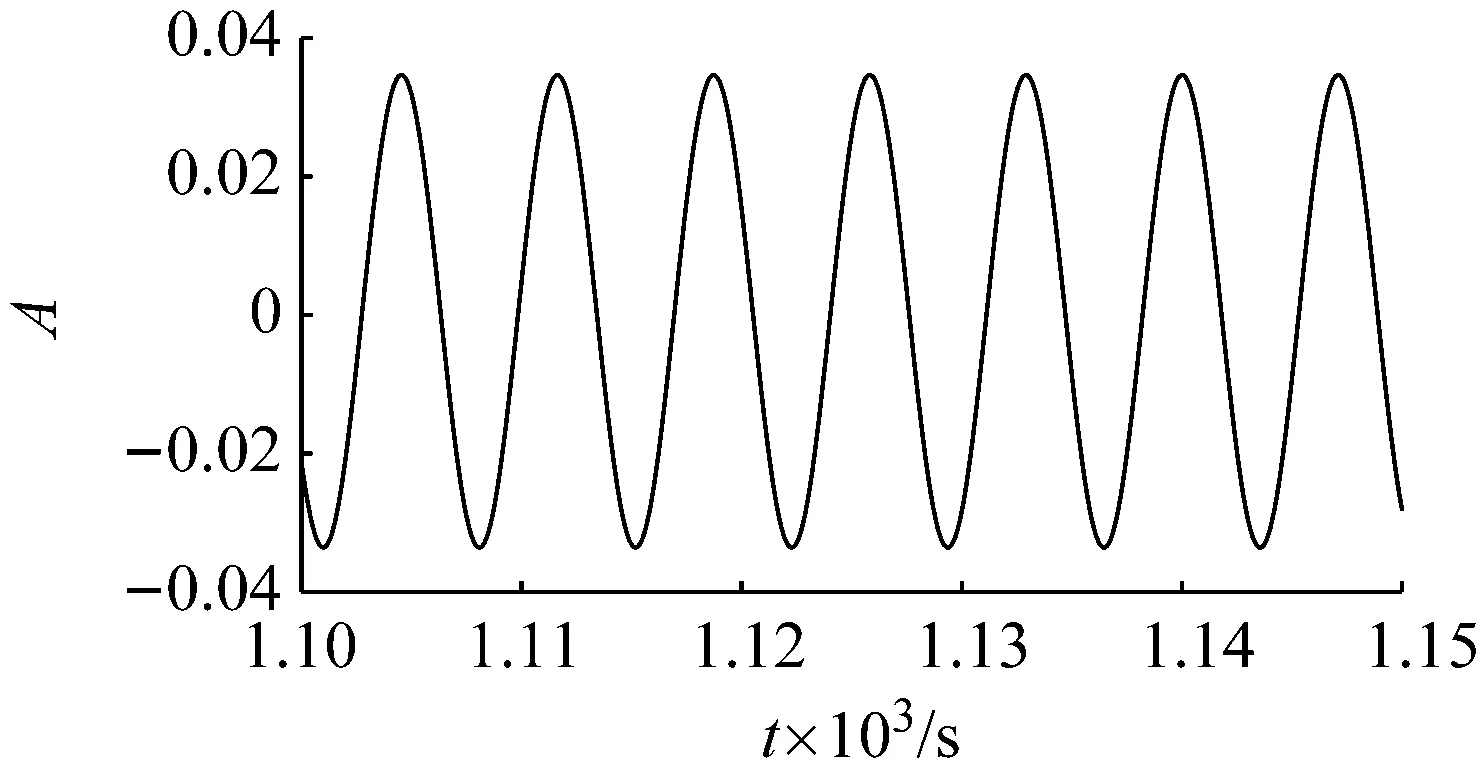
(a)时域信号

(b)频域信号图9 激励频率为0.141 Hz，激励幅值为0.02的响应信号Fig.9 The response signal with excitation frequency 0.141 Hz and excitation amplitude 0.2

对比图4和图8以及对比图5和图9可知，图8和图9在激励频率满足亚谐波产生的所需激励频率条件时，激励幅值显然小于亚谐波产生的阈值。据此可知，亚谐波共振不仅与激励频率有关，而且与激励幅值有关，亚谐波共振产生的另一激励条件为激励幅值大于亚谐波产生的阈值。

2 黏接界面脱黏的实验研究

2.1 实验装置

理论分析和仿真的结果表明黏接界面脱黏时，作用一定幅值和频率的激励信号，频谱中出现亚谐波信号。为进一步验证亚谐波共振方法识别黏接界面脱黏的有效性，进行了黏接界面脱黏的识别实验。实验装置如图10(a)所示，试件为两块铝板(350 mm×80 mm×2 mm)用环氧树脂AB胶黏接的铝梁结构，黏接区域80 mm×80 mm，胶层厚度0.5 mm，如图10(c)所示。试件在室温自然固化24 h后，在疲劳试验机上循环加载产生界面脱黏。试件两端施加固定约束，对试件黏接区域以0.2～10 kN/5 Hz连续加载48小时，铝梁黏接区域局部发生界面脱黏如图10(b)所示。试件表面黏贴两个压电片(SMD12)，压电片直径12 mm，厚0.7 mm，间隔350 mm。试件黏接区域处于两个压电片正中。试件两端放置海绵模拟自由边界。采用信号发生器(Agilent33522A)输出正弦信号，输出信号通过电压放大器(TEGAM2350)放大后作用于一个压电片上，用示波器(AgilentD50-X3014A)从另一个压电片采集响应数据。

(a)实验装置

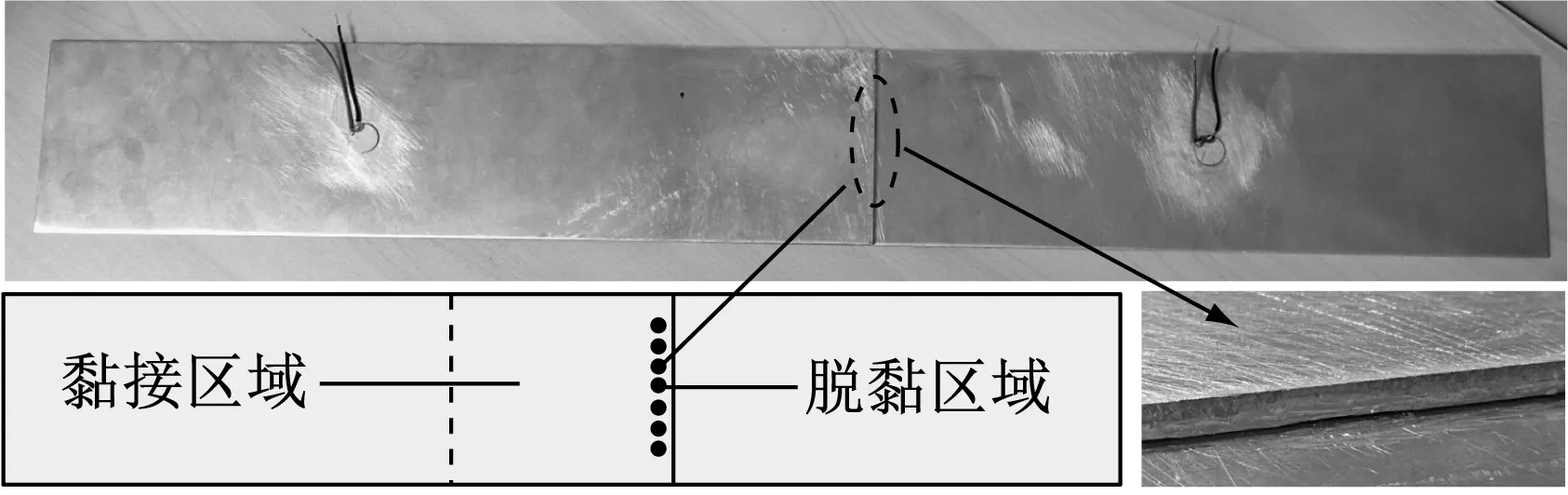
(b)试件

(c)试件尺寸图10 实验装置、试件及试件尺寸Fig.10 The experiment equipment，specimen and specimen size

2.2 实验过程

试件未经过疲劳加载前，试件处于无损状态，试件两端放置海绵模拟自由边界，信号发生器任取激励频率50 kHz幅值为50 V的正弦激励作用于作动压电片上，得到响应的频谱图如图11所示。

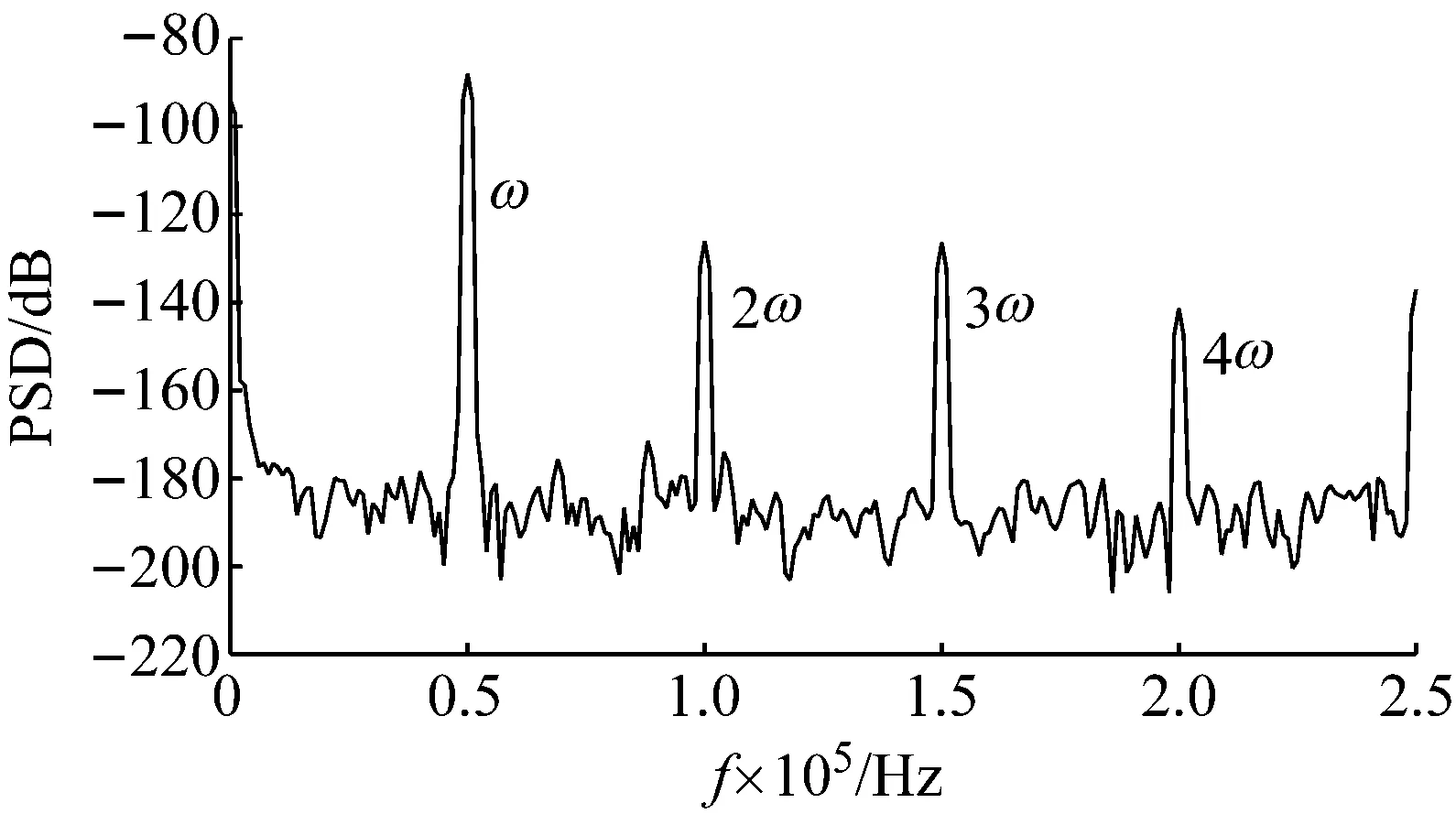
图11 完整试件频谱图(激励频率50 kHz激励幅值50 V)Fig.11 Spectrum of undamaged specimen (excitation frequency 50 kHz and excitation amplitude 50 V)

从图11中可以看出尽管试件在无损状态下是线性结构，理论上响应的频谱中没有超谐波成分产生，但由于测量环节的影响，实验结果响应频谱图中出现了二倍激励频率和三倍激励频率的超谐波成分。

试件经过疲劳加载后，局部明显脱黏，破坏了结构的完整性。脱黏引起黏接界面刚度发生变化，而呈现平方和立方非线性刚度[18]。由理论分析和仿真结果可知，当系统含平方和立方非线性项时，激励频率接近两倍或三倍固有频率激励幅值满足阈值条件，会发生亚谐波共振现象。

试件局部脱黏状态下，试件两端放置海绵模拟自由边界，信号发生器输出频率范围为10到50 kHz的线性扫频激励，激励幅值为50 V，得到扫频激励下的频谱图，如12所示。由图12频域峰值得到试件的某阶纵向固有频率约为33.2 kHz。

图12 试件扫频图(激励频率10～50 kHz激励幅值50 V)Fig.12 The response signal with sweep excitation (excitation frequency 10-50 kHz and excitation amplitude 50 V)

由理论分析和仿真结果可知，激励频率接近三倍固有频率时，会发生亚谐波共振。激励幅值设定为50 V，激励频率取三倍固有频率99.6 kHz，得到的响应信号的频谱图，如图13所示。由图13可知，响应结果中不仅出现了两倍激励频率(199.2 kHz)的谐波成分，而且明显出现了1/3激励频率(33.2 kHz)、2/3激励频率(66.4 kHz)的亚谐波以及4/3激励频率(132.8 kHz)、5/3激励频率(166 kHz)的超亚谐波成分。

图13 试件黏接界面脱黏状态下频谱图(激励频率99.6 kHz，激励幅值50 V)Fig.13 Spectrum of damaged specimen (excitation frequency 99.6 kHz and excitation amplitude 50 V)

对比图11和图13，两者结果均有超谐波成分产生，而图11黏接界面完好，图13黏接界面出现明显脱黏，说明实际检测结果的高次谐波不完全由黏接界面处缺陷产生，受到了测量环节非线性的影响。亚谐波成分只有在固体界面处的冲击碰撞与振动接触时产生，可以认定图13响应结果中出现的亚谐波成分只是由黏接界面处缺陷非线性造成的。

由仿真结果可知，亚谐波的产生与激励幅值有关。将激励幅值设定为25 V，即图13激励幅值的二分之一，激励频率为三倍固有频率99.6 kHz，得到的响应信号的频谱图如图14所示。由图14可知，响应结果中只出现两倍激励频率(199.2 kHz)等超谐波成分。

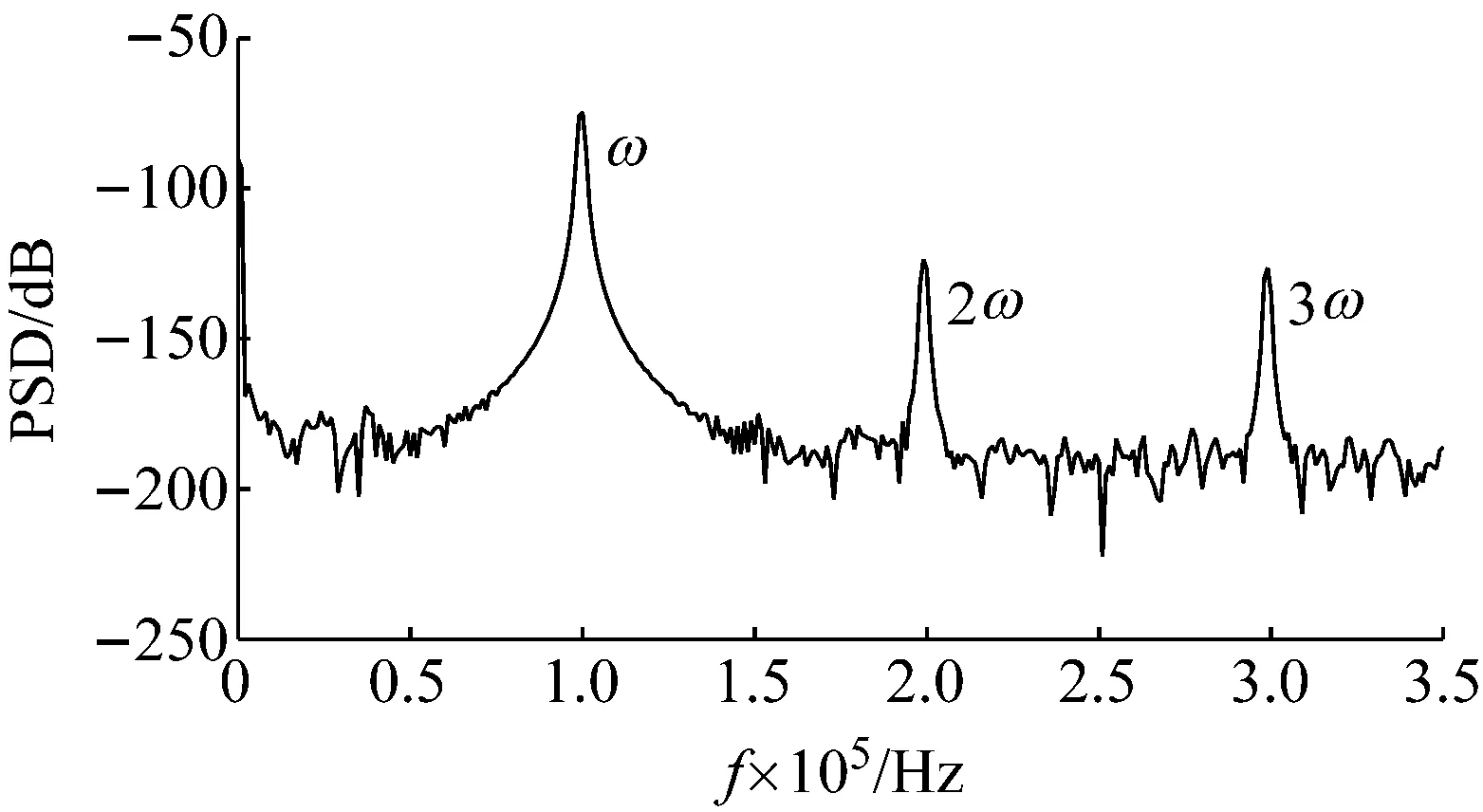
图14 试件黏接界面脱黏状态下频谱图(激励频率99.6 kHz，激励幅值25 V)Fig.14 Spectrum of damaged specimen (excitation frequency 99.6 kHz and excitation amplitude 25 V)

对比图13和图14，激励频率一定时，激励幅值为25 V时，频谱中没有亚谐波成分，而谐波成分依然明显，说明激励幅值没有达到亚谐波产生阈值。图13中亚谐波成分明显，说明50 V已经达到产生亚谐波的阈值。因此，激励幅值只有达到亚谐波产生的阈值时，才会发生亚谐波共振。

由理论分析和仿真结果可知，激励频率接近两倍固有频率时，也会发生亚谐波共振。激励幅值设定为50 V，激励频率以66.4 kHz为中心，0.1 kHz为步长逐步增加频率至68.4 kHz，逐步减低频率至64.4 kHz，得到64.4～68.4 kHz范围内亚谐波成分最明显的激励频率68.0 kHz。激励频率取接近二倍固有频率68.0 kHz，激励幅值设定为50 V得到的响应信号频谱图如图15所示。由图15可知，响应结果中不仅出现了两倍激励频率(136 kHz)等谐波成分，而且明显出现了1/2激励频率(34.0 kHz)的亚谐波成分。

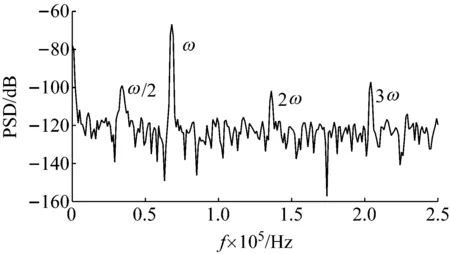
图15 试件黏接界面脱黏状态下频谱图(激励频率68.0 kHz，激励幅值50 V)Fig.15 Spectrum of damaged specimen (excitation frequency 68.0 kHz and excitation amplitude 50 V)

对比图11和图15，两者均出现明显谐波成分，与图11不同，图15出现明显亚谐波成分，可以得出后者结果出现的亚谐波成分是由黏接界面处缺陷非线性造成的。

由仿真结果可知，亚谐波的产生与激励幅值有关。激励幅值设定为25 V，即图15激励幅值的二分之一，激励频率为接近两倍固有频率68.0 kHz，得到响应信号的频谱图如图16所示。由图16可知，响应结果中只出现两倍激励频率(136 kHz)等超谐波成分。

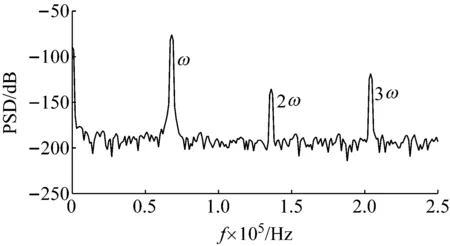
图16 试件黏接界面脱黏状态下频谱图(激励频率68.0 kHz，激励幅值25 V)Fig.16 Spectrum of damaged specimen (excitation frequency 68.0 kHz and excitation amplitude 25 V)

对比图15与图16，激励频率相同而激励幅值不同时，两者结果均出现超谐波成分，前者结果中还出现了亚谐波成分，表明利用1/2亚谐波共振识别界面脱黏损伤需要激励幅值达到亚谐波产生的阈值。

理论分析和仿真结果表明，亚谐波产生需要特定激励频率条件。激励幅值设定为与图13和图15相同激励幅值50 V，任取远离两倍和三倍固有频率的激励频率40 kHz，得到的响应信号的频谱图如图17所示。由图17可知，响应结果中只出现两倍激励频率(80 kHz)等谐波成分。

图17 试件黏接界面脱黏状态下频谱图(激励频率40 kHz，激励幅值50 V)Fig.17 Spectrum of damaged specimen (excitation frequency 40 kHz and excitation amplitude 50 V)

对比图13、图15和图17，激励幅值相同时，激励频率接近三倍固有频率或接近两倍固有频率时，才会发生亚谐波共振。由此验证了利用亚谐波方法识别界面脱黏激励频率条件是激励频率接近三倍固有频率或两倍固有频率。

3 结 论

本文建立了黏接界面的单自由度非线性模型，推导了亚谐波共振在单频激励下的激励频率条件，并对黏接界面非线性模型进行了数值仿真以及对铝板黏接结构进行了黏接界面脱黏的亚谐波共振识别实验。理论分析、仿真和实验结果验证了亚谐波方法识别黏接界面脱黏需要特定的激励条件，即激励频率接近两倍或三倍固有频率，激励幅值达到亚谐波产生的阈值。利用非线性超声超谐波检测黏接界面脱黏容易受到测量环节的影响，易产生损伤误报，不能准确识别界面脱黏。亚谐波产生不受测量环节的非线性影响，只对黏接界面缺陷的非线性特征敏感，使用亚谐波方法能有效识别黏接界面脱黏。

本文是利用响应频谱中是否出现亚谐波成分来判定黏接界面是否脱黏，但不能对具体脱黏区域进行定位以及对脱黏区域面积进行估算，有待进一步研究。