基于BP神经网络辅助的惯性/天文组合导航方法
孙洪驰,穆荣军,杜华军,崔乃刚
(1.哈尔滨工业大学 航天学院,哈尔滨 150001;2.北京航天自动控制研究所,北京 100854; 3.宇航智能控制技术国家级重点实验室,北京 100854)
天文导航作为一种高可靠、无累积误差、高精度的导航方式,在航天、航空等领域得到广泛的应用[1]。得益于星敏感器较高的天文测量结果,惯性/天文组合导航系统通常可以达到角秒级的姿态估计精度[2-3]。但在环境比较复杂的条件下,常规惯性/天文组合导航系统会不可避免地受到影响,诸如复杂姿态机动、恶劣气动环境等因素,都会造成导航误差的增大,且目前对于这些影响尚没有较为成熟且精确的建模、补偿和修正方法[4-5]。
近年来随着神经网络理论的完善和人工智能技术的发展,为如何提高复杂动态环境下的惯性/天文组合导航精度提供了一种新的思路[6-7]。将神经网络技术 应用于组合导航领域,虽然目前尚没有较为完善的理论,但神经网络在各个领域所展现出的优越性能和发展潜力吸引了很多学者[8-10]。陈鑫鑫等人采用神经网络预测失锁时的GPS导航结果,有效解决了卫星失锁条件下的组合导航问题,但组合导航系统本身的滤波估计精度并没有进一步的提升[11];李松等学者对基于BP(Back Propagation)神经网络辅助的导航滤波方法进行了初步的探索和论证,并提出了利用滤波残差和增益进行网络训练的方法[12]。但在对这些方法进行前期复现过程中发现,进行惯性/天文组合导航时,利用滤波残差对神经网络进行训练效果并不明显。采用滤波增益矩阵虽然可以取得较好的效果,但增益矩阵元素过多,以惯性/天文组合导航为例,滤波增益矩阵为3×15维,则要求至少45个输入层神经元,这将导致训练速度过慢,算法过于冗余。同时由于神经网络中没有输入与动态环境相关的物理参数,这也导致这种方法并不具备对复杂动态环境的适应能力。
结合目前惯性/天文组合导航领域面临的主要问题和近年来神经网络技术的发展趋势[13-15],明确主要研究目标包括以下三点:
① 在传统惯性/天文组合导航方法的基础上引入神经网络辅助修正环节,进一步提高组合导航的姿态估计精度;
② 完善并优化神经网络训练环节,选取合理的特征向量构建方式,尽可能减少网络的冗余计算量,提高训练效率;
③ 在前两条的基础上引入惯性器件测量参数,利用神经网络技术解决高动态环境下惯性天文组合导航精度下降的问题。
1 惯性/天文组合导航模型
惯性/天文组合导航系统通常选用捷联惯导的误差传播方程作为状态方程,选取“东北天”地理坐标 系为导航系,取姿态失准角(φx,φy,φz)、速度、位置和陀螺常值漂移(εx,εy,εz)、加计常值偏置( ∇x,∇y,∇z)为状态量。系统的状态方程可以表示为:

其中,F(t)为系统的状态转移矩阵,G(t)为系统的噪声驱动矩阵,w(t)为系统噪声矢量。
将状态方程离散化并忽略高阶项后,可以得到k时刻系统的状态方程为:
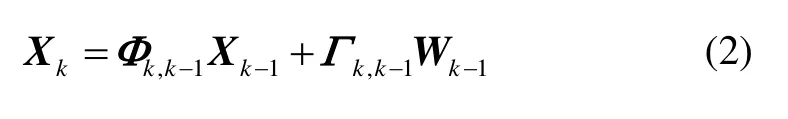
其中,Φk,k-1、Γk,k-1为离散化后的状态转移矩阵和噪声驱动矩阵。设滤波周期为T,则Φk,k-1、Γk,k-1可以表示为:

组合导航系统以惯导和星敏感器测量得到的姿态差构建量测量。但由于惯性//天文组合导航系统的状态量为平台失准角,需要将姿态误差角换成平台失准角后才能作为卡尔曼滤波器的观测量。
假设惯导和星敏感器测量得到的姿态(转序:偏航、俯仰、滚转)分别为φi、θi、γi和φc、θc、γc,则平台失准角可以表示为:
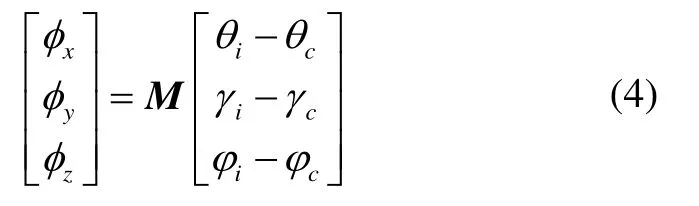
其中,M为姿态误差角到平台失准角的转换矩阵,在“东北天”坐标系下其具体形式为:

取量测量Z=[φxφ yφz]T,则量测方程可以表示为:

其中,H为量测矩阵,V(t)为测量噪声。
根据上述状态方程和量测方程,通过卡尔曼滤波进行惯性、天文组合导航信息估计,具体公式如式(7)所示:
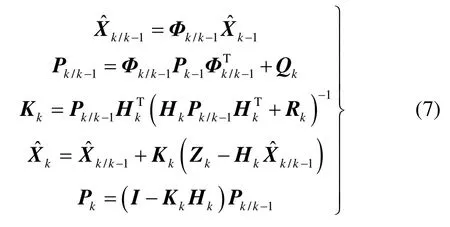
式中,Qk和Rk分别为状态模型和量测模型噪声方差阵。
2 基于BP神经网络的组合导航系统设计
2.1 基于QR分解的神经网络特征向量构建方法
BP神经网络由输入层、隐含层和输出层组成,输入层和隐含层采用全连接的方式。为提高对非线性系统的适应能力,隐含层通常采用losig函数作为激活函数,利用误差反向传播算法更新节点连接权值。BP神经网络作为最常用的人工神经网络,其基本理论已经十分成熟,对于神经网络在组合导航领域的应用,需要解决的问题主要集中在特征向量的构建方法上。
通过国内外相关文献的调研分析,目前基于神经网络辅助的组合导航系统主要采用滤波残差、增益来构建特征向量。但在前期对这些方法进行复现的过程中发现,对于惯性/天文组合导航系统,采用滤波残差构建的特征向量对神经网络进行训练的效果并不理想。采用滤波增益构建特征向量进行训练虽可以达到理想的效果,但由于组合导航系统状态量维数较大,滤波增益矩阵元素过多,训练速度十分缓慢。
为解决这些问题,对式(7)中的滤波增益矩阵Kk进行QR分解,将Kk分解成Q15×15和R15×3两个矩阵的乘积,具体形式如式(8)所示:

将增益矩阵Kk进行QR分解后,提取R阵中的非零元素构建神经网络的输入特征向量,由式(8)可知,此时仅需要6个元素即可实现神经网络特征向量的构建这说明利用QR分解提取增益矩阵的主要特征,可以有效地降低神经网络特征向量的维数,在不影响算法性能的前提下,有效提高了BP神经网络的训练速度和组合导航算法的计算效率。
同时,针对动态环境下组合导航精度下降的问题,在6维特征向量的基础上,额外加入惯导系统测量得到的角速度信息构建9维特征向量引入动态环境下的惯性测量参数, 可以进一步提高惯性/天文组合导航系统在动态环境下的适应能力。
2.2 基于BP神经网络辅助的卡尔曼滤波器设计
采用基于QR分解的神经网络特征向量构建方法,可以有效降低输入层神经元个数,大大提高了网络的训练速度。BP神经网络结构如图1所示。

图1 BP神经网络结构 Fig.1 Structure of BP neural network
输入特征向量为9维,其中包括6维增益矩阵特征元素和3维角速度信息(非高动态环境下可去掉后三维进一步精简)。设置隐含层10个神经元,采用losig激活函数,输出层神经元3个,采用purelin函数线性输出。BP网络输出量的物理意义为姿态估计误差,即:

在完成网络训练后,即可利用BP神经网络的输出信息辅助修正组合导航的滤波估计结果,整个系统构成如图2所示。
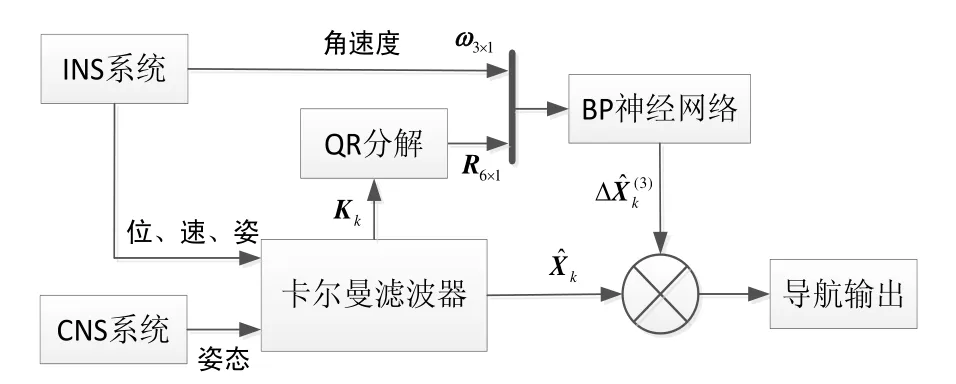
图2 基于BP神经网络的卡尔曼滤波算法流程图 Fig.2 Flow chart of Kalman filtering base on BP neural network
在常规卡尔曼滤波算法的基础上,加入BP神经网络修正环节。首先对滤波增益Kk进行QR分解,提取R阵中非零元素与角速度一起构建BP网络的输入特征向量。然后利用网络的输出结果辅助修正滤波估计值,进一步提高组合导航系统的估计精度和对动态环境的适应能力。
3 仿真验证
为验证基于BP神经网络辅助的惯性/天文组合导航算法的有效性,通过两组仿真实验进行论证。对比不同工况下基于BP神经网络辅助的卡尔曼滤波算法(Back Propagation Kalman Filtering,BPKF)与常规卡尔曼滤波算法(Kalman Filtering,KF)的估计精度。
3.1 仿真实验1
仿真实验1主要验证基于滤波增益矩阵QR分解的神经网络特征向量构建方法的可行性。验证QR分解法能否在不影响导航精度的情况下有效缩减输入向量维度,提高算法的计算效率。仿真时间设置150 s,轨迹设置为匀速平飞,惯导和星敏器件精度如表1所示。
首先直接利用滤波增益矩阵(不采用QR分解法)构建特征向量,此时网络输入为45维,仿真结果如图3所示。
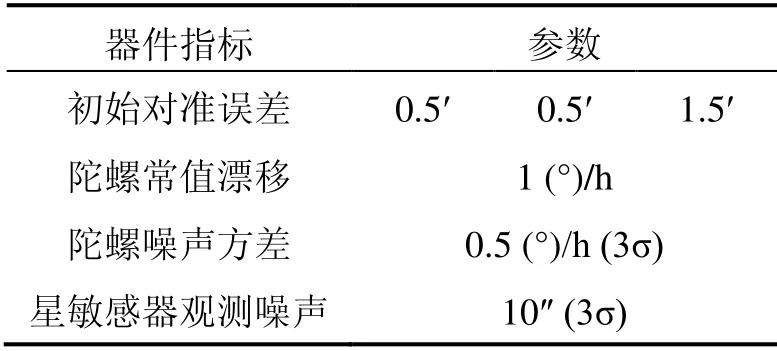
表1 仿真器件参数 Tab.1 Parameters of simulated device
虽然此时BPKF算法精度优于常规KF算法,但由于未对滤波增益矩阵进行精简,导致BP网络的输入神经元数目过多,计算耗时过大。BP神经网络单次训练平均耗时及组合导航滤波估计精度如表2所示。
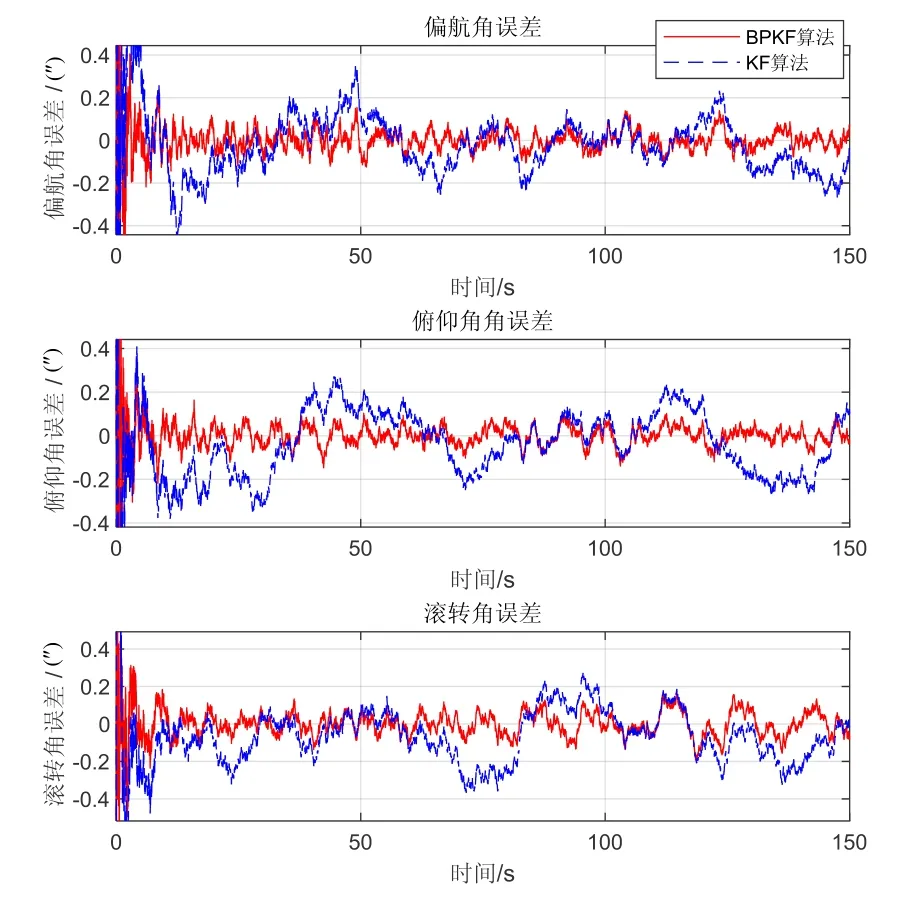
图3 BPKF算法与常规KF算法滤波精度对比(无QR分解) Fig.3 Comparison on filtering accuracy between BPKF and KF (without QR decomposition)

表2 未采用QR分解法条件下仿真结果统计 Tab.2 Statistics of simulation results without QR decomposition
然后利用QR分解提取增益矩阵主元素进行仿真,仿真结果如图4所示。
BP神经网络单次训练平均耗时及组合导航滤波估计精度如表3所示。
对比图 3与图 4和表 2与表 3可以得出以下结论:
① 无论是否采用QR分解,BPKF算法精度均优于常规KF算法,姿态估计精度可以提高30%以上。

图4 BPKF算法与常规KF算法滤波精度对比(采用QR分解) Fig.4 Comparison on filtering accuracies between BPKF and KF (with QR decomposition)
② 采用QR分解后,将BP网络的输入向量由45维 减少到6维,网络规模显著减小,单次平均训练时间由0.3038 s 缩短到0.0418 s,提高了一个量级。
③ 采用QR分解对滤波增益矩阵进行精简,滤波估计精度并没有下降反而略有提高,这说明QR分解法可以有效保留滤波增益矩阵的特征,同时也说明输入元素的维度并非越大越好,过多的特征向量反而会引起网络的过拟合问题从而导致BPKF算法精度下降。

表3 采用QR分解法条件下仿真结果统计 Tab.3 Statistics of simulation results with QR decomposition
3.2 仿真实验2
仿真实验2主要验证动态环境下引入角速度信息构建特征向量能否有效提高组合导航系统的滤波估计精度。仿真时间设定为150 s,偏航方向持续进行无规律S型机动,俯仰、滚转轴保持静止作为参照。偏航方向姿态机动曲线如图 5所示。
首先验证在不引入角速度信息时,仅利用增益矩阵进行BPKF滤波能否保证动态条件下的组合导航精度,仿真结果如图6所示。
从图6中大致可以看出,在偏航轴进行复杂机动时,姿态估计精度会出现下降。为了更直观比较动态环境下两种滤波方法性能,对前50 s偏航角估计结果进行放大,估计结果如图7所示。
组合导航滤波估计精度如表4所示。

图5 偏航角机动曲线 Fig.5 Maneuver curve of yaw angle
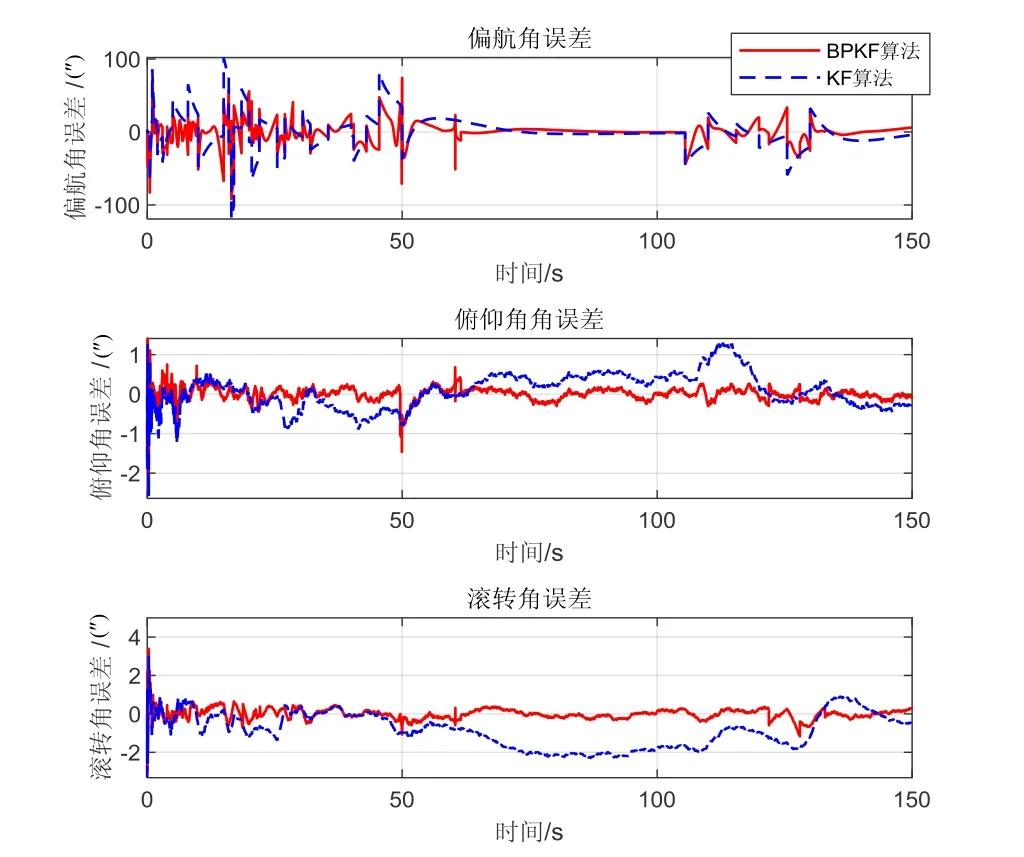
图6 BPKF算法与KF算法滤波精度对比(未引入角速度) Fig.6 Comparison on filtering accuracies between BPKF and KF (without angular velocity)

图7 前50 s偏航角估计精度对比放大图(未引入角速度) Fig.7 Partial enlarged drawing of yaw angle error in the first 50 s (without angular velocity)

表4 未引入角速度时仿真结果统计 Tab.4 Statistics of simulation results without angular velocity
然后在增益矩阵的基础上额外引入角速度信息,构建9维特征向量对BP神经网络进行训练。仿真结果如图8所示。
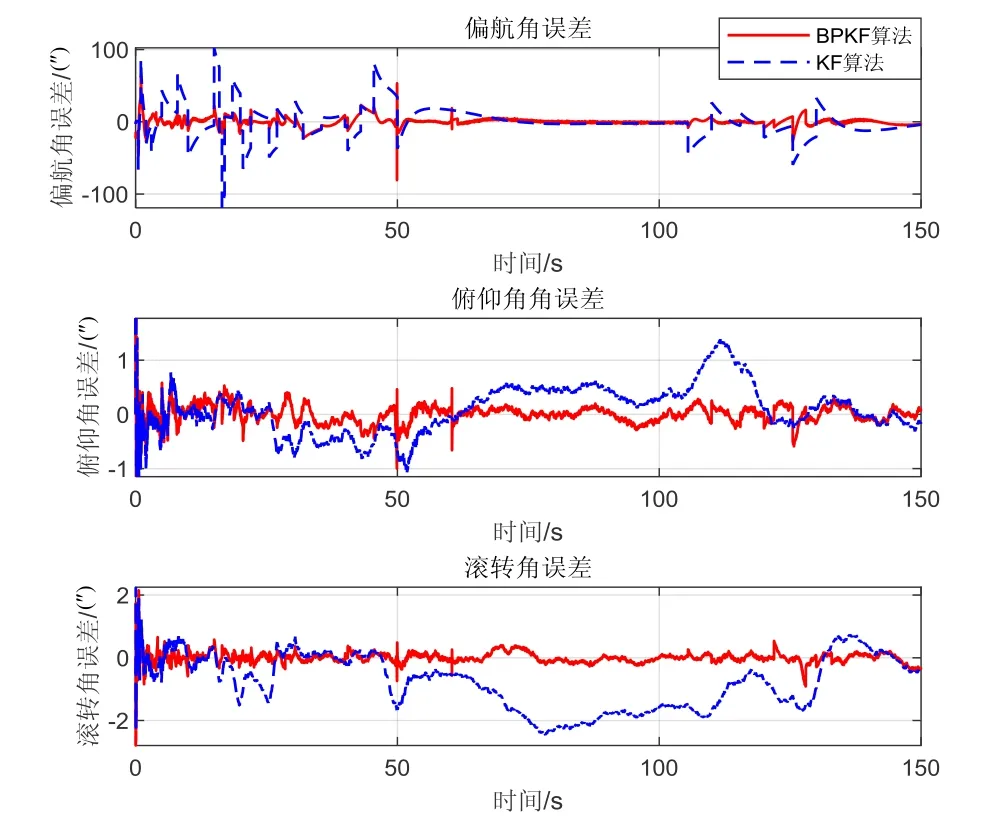
图8 BPKF算法与KF算法滤波精度对比(引入角速度后) Fig.8 Filtering accuracy comparison between BPKF and KF (with angular velocity)
对比图6和图8中可以看出,引入角速度信息后偏航轴姿态精度提升明显,这说明采用角速度信息构建特征向量对BP网络进行训练,使组合导航系统的动态性能有了很大的提高。为了更直观地比较动态环境下引入角速度信息后BPKF算法的动态性能,对前50 s偏航角估计结果进行放大,如图9所示。
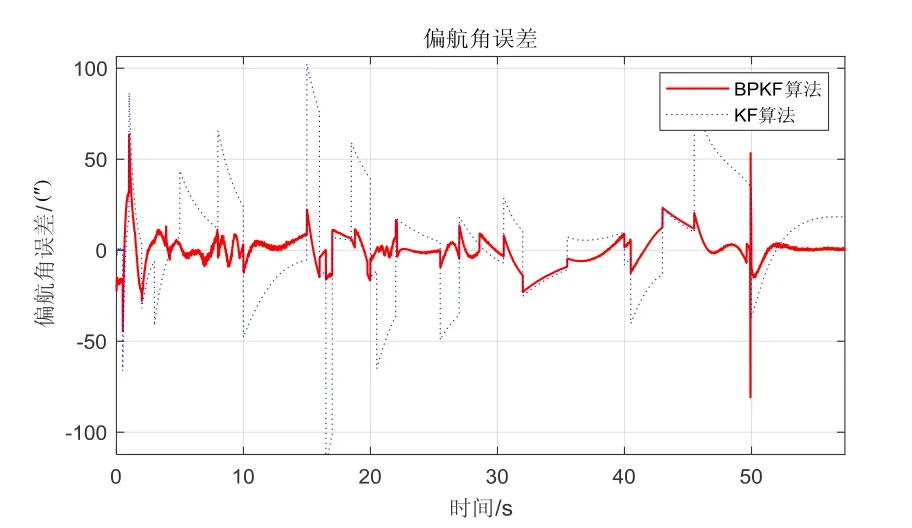
图9 前50 s偏航角估计精度对比放大图(引入角速度后) Fig.9 Partial enlarged drawing of yaw angle error in the first 50 s (with angular velocity)
组合导航滤波估计精度如表5所示。

表5 引入角速度后仿真结果统计 Tab.5 Statistics of simulation results with angular velocity
从仿真中可以看出,在高动态环境下,引入角速度信息后的BPKF算法可以有效提高组合导航精度。对比图7和图9,若不引入角速度信息,仅靠滤波增益矩阵无法有效提高动态环境下的滤波估计精度。引入角速度信息后,即使是在姿态变化非常剧烈的条件下,采用基于BP神经网络辅助的惯性/天文组合导航算法依然可以保证较为精确的姿态精度,动态环境下姿态误差可以保证在5″(1σ)以内。
4 结 论
基于BP神经网络辅助的惯性/天文组合导航方法,利用QR分解提取滤波增益矩阵的主元素构建神经网络的特征向量,采用BP神经网络辅助修正卡尔曼滤波估计结果,进一步提高惯性/天文组合导航方法的精度。针对复杂动态环境下滤波估计精度下降的问题,引入角速度信息进行BP网络的训练,经过仿真验证,相较于传统方法,采用神经网络辅助的组合导航系统可以达到更高的导航精度和更强的动态适应能力,可以有效提高动态环境下的惯性/天文组合导航精度,对未来组合导航领域的发展具有一定的参考价值。

