基于因子图的AUV多传感器组合导航算法

马晓爽，刘锡祥，张同伟，刘贤俊，许广富

（1.东南大学 仪器科学与工程学院，南京 210096；2.微惯性仪表与先进导航技术教育部重点实验室，南京 210096；3.国家深海基地管理中心，青岛 266237）

对于自主水下航行器（Autonomous Underwater Vehicle,AUV）而言，随着水下导航传感器的数量和种类不断增加，怎样有效融合多种导航传感器提供的量测信息来提高水下组合导航精度一直是国内外备受关注的研究重点[1-2]。国内外众多研究学者已经对水下组合导航信息融合技术做了大量的工作，并在导航精度上有了一定的提高。而分布式结构的联邦卡尔曼滤波技术及其各类改进方法以其容错性好、计算量小、设计灵活等特点在多源信息融合技术中应用最为广泛，尤其是在水下导航领域中[3]。

文献[4]利用分布式的联邦卡尔曼滤波技术有效提高了AUV“T1”的导航性能，避免了单一传感器的局限性。文献[5]提出了一种基于联邦滤波的地形辅助捷联惯导系统并应用于水下航行器中，能够提高长航导航的精度和可靠性。文献[6]在联邦卡尔曼滤波的基础上，引入了一个基于奇异值分解的动态信息共享因子，既解决了传统联邦滤波器信息分配因子的盲目性，又减少了计算量。

然而，各导航传感器的信息更新频率通常异步，而联邦卡尔曼滤波只能等待所有传感器的量测信息全部到达之后才可以进行信息融合，这无疑会对AUV 组合导航系统的精度和实时性造成影响。而且AUV 水下作业环境复杂多变，外部干扰的统计特性具有不确定性，在不能满足其假设的前提下，亦会对联邦卡尔曼滤波的导航性能造成影响。另外，某些导航传感器通常会由于一些特殊原因出现不活跃甚至失效的情况，或者只在短时间内有信号，这时联邦卡尔曼滤波方法就会面临信息故障以及信息源变化后的系统重构等难题。

针对以上问题，本文提出了一种基于因子图的多传感器组合导航算法，并应用于AUV 水下组合导航系统。因子图作为一种概率图模型，最早应用于编码领域，目前在人工智能、信号处理、神经网络等领域也逐渐开始使用因子图方法来解决一系列复杂问题。因子图方法为导航系统的信息融合提供了一个新思路。它可以将可用导航传感器的量测信息抽象成相应的因子节点，根据非线性优化理论对状态变量节点进行递推与更新，能够实现惯性导航系统与不同导航传感器的非等间隔融合，满足不同类型水下导航传感器的即插即用。

1 因子图算法

因子图[7-8]是用来表达随机变量的联合概率分布的二分图模型G=(F,X ,E)。它包括两类节点：一类是因子节点fi∈F，是指因式分解中的局部函数；另一类是变量节点x j∈X，是指全局多元函数中的变量。边缘eij∈E是指当且仅当因子节点fi与状态变量 节点xj相关时存在一条连接边。

那么因子图G就可以定义为函数f(X)的因式分 解[9-10]：其中X是与因子节点xi有 关的所有变量节点的集合。我们通常将每一个因子f i(xi)表示成一个误差函数fi(xi) =d(erri(xi,zi))，其 中d(·) 代表相应的代价函数，zi是实际量测值。

我们可以将因子图的概念引入AUV 多源导航系统的信息融合问题中，用变量节点xi表示AUV 在ti时刻的导航状态，并定义当前时刻tk的导航状态集用zi表示ti时刻由不同导航传感器得到的实际量测信息，并定义当前时刻tk的量测集由此定义得到所有状态变量和量测的联合概率密度（Probability Distribution Function,PDF）及其因式分解可表示为：

其中，P(x0)表示所有变量的初始状态的先验信息；表示量测模型中变量节点的一个集合；ziIMU是为了区分来自惯性组件IMU 的量测信息，用于描述一个过程模型P(xi|xi-1,ziIMU)。

在联合概率密度函数P(X k|Zk)的因式分解中，每个因子都代表一个独立的项，即，

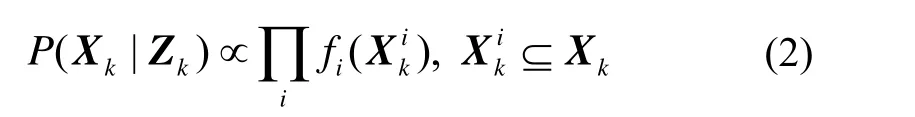
对于高斯噪声分布，我们可将每一个代表量测模型的因子fi表示成一个误差函数：

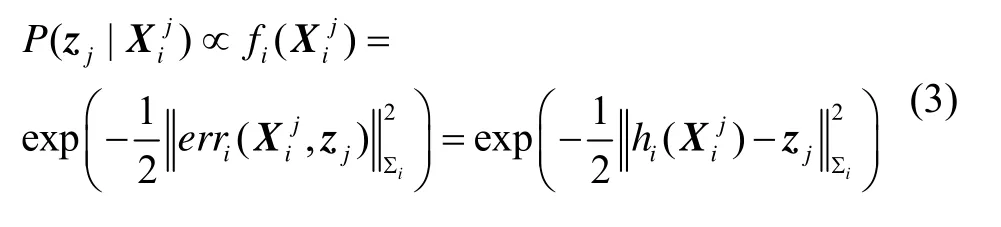
将每一个代表过程模型的因子fi表示成一个误差函数：

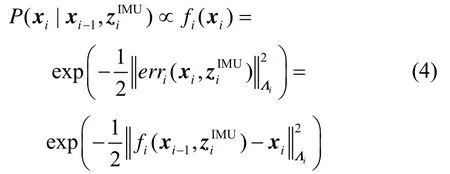
为了根据所有可用量测信息获得所有状态变量的最优估计，我们可以通过最大后验概率密度（Maxi- mum a Posteriori,MAP）估计，将AUV 多传感器信息问题转化为一个等价的非线性优化问题。此时，对式(1)取负对数的最小值可以获得所有状态变量的最大后验概率密度估计X*，即：

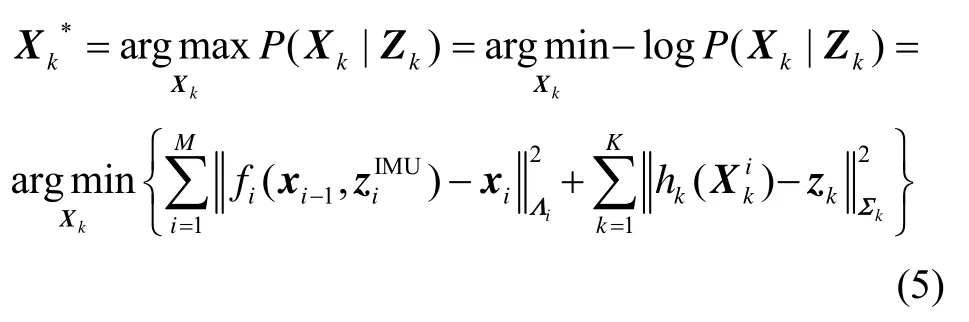
为了简单起见，在这里我们略去了之前的先验信息P(x0)。根据非线性优化理论[12]，通过调整变量Xk使之最小化，那么这个最优估计值Xk*就可以使整个误差f(X)最小。

2 基于因子图的AUV 多传感器信息融合框架

由于AUV 实际工作环境及其自身一些特点，本文采用捷联惯性导航系统（Strapdown Inertial Navigation System,SINS）、多普勒计程仪（Doppler Velocity Log,DVL）、磁航向仪（Magnetic Compass Pilot,MCP）以及地形辅助导航设备（Terrain Aided Navigation,TAN）作为导航设备来实现AUV 的高精确导航定位[13-14]。水下航行器组合导航系统的高度信息通常采用深度计（Depth Meter,DM）来测量，这是由于惯性导航系统的垂直通道不稳定，而且多普勒计程仪输出的垂直速度信息也相对不准确，因此本文不对垂直通道作讨论。图1为AUV 多源信息融合的因子图框架，定义AUV水下组合导航系统在ti时刻的状态变量xi为变量节点，包括AUV 的失准角、速度误差、位置误差以及惯性仪表误差状态量，即x=[ΦδVδPε ∇]T，将IMU、DVL、MCP、TAN 导航传感器的量测信息抽象成相对应的因子节点fIMU、fDVL、fMCP、fTAN。图1中IMU 是SINS 的测量单元，后文对SINS 与IMU 不加以区分。

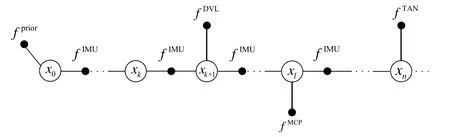
图1 基于因子图的AUV 多源信息融合框架 Fig.1 Framework of AUV multi-source information fusion based on factor graph

2.1 IMU 因子节点

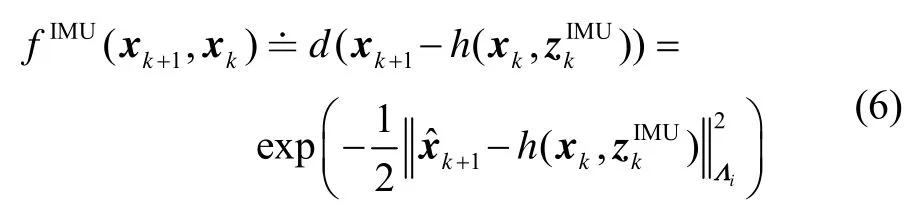
式(5)即为IMU 因子节点的表达式。当在因子图中添加新的变量节点xk+1时，需要合理的，这个值可以从预测中得到。

2.2 DVL 因子节点

DVL 量测方程可以表示为：

其中，nDVL是量测噪声，hDVL是量测函数。

在tm时刻接收到DVL 量测信息后，添加新的因子节点fDVL。DVL 因子节点只与变量节点xm，即tm时刻的导航状态相关。因此，可以将因子节点fDVL定义为一个一元边因子：

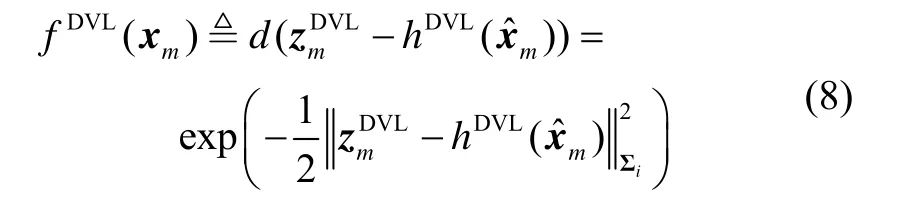
随着时间的推移，在其他时刻接收到MCP、TAN传感器的量测信息后，定义因子节点fMCP、fTAN扩展因子图，根据不同传感器的量测方程以及利用相应的代价函数进行变量节点的递推和更新。当传感器可用性发生改变时，只需在因子图模型中删除或加入因子节点，便可以实现AUV 组合导航系统工作模式的无缝切换。

3 基于因子图与联邦滤波的融合过程比较分析

目前大多采用无反馈模式的联邦卡尔曼滤波算法以提高AUV 组合导航系统的容错性能[13,15]。以SINS 作为公共参考系统，3 个子滤波器分别为SINS/ DVL、SINS/TAN、SINS/MCP，均采用标准的卡尔曼滤波结构，各子滤波器独立工作，仅在主滤波器中进行信息融合。AUV 多源信息融合联邦卡尔曼滤波器结构图如图2所示。

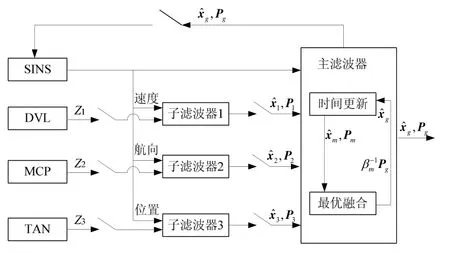
图2 联邦卡尔曼滤波器结构图 Fig.2 Structure of the federal Kalman filter

无反馈模式的联邦卡尔曼滤波器能够有效避免由于某个子滤波器出现故障而污染到其他子滤波器的情况，提高系统的容错性能。但是当某个传感器故障或失效时，需对其相应子滤波器单独隔离并进行系统重构，大大降低了其灵活性和扩展性。

而因子图方法完全不需要针对传感器异步问题与可用性时变问题进行调整，每接收一次传感器量测信息，可将其抽象成因子节点连接到对应的变量节点，当某个传感器失效时，可拒绝加入该因子节点至因子图中。比如，DVL 信号失效时，AUV 组合导航系统由SINS/DVL/TAN/MCP 工作模式切换为SINS/TAN/MCP工作模式，此时因子图模型删除了因子节点fDVL，速度误差得不到修正，其精度会降低，从而导致位置误差精度也有所下降；而DVL 信号重新有效时，AUV 组合导航系统由 SINS/TAN/MCP 工作模式切换为SINS/DVL/TAN/MCP 工作模式，此时因子节点fDVL又被重新添加进因子图中，速度误差将会得到修正。其他传感器与DVL 情况类似，在这里不再赘述。因此基于因子图的方法可以简单地通过增减对应导航传感器的因子节点实现即插即用功能，与联邦滤波算法相比，因子图算法具有更好的灵活性和可扩展性。

4 试验结果与分析

4.1 仿真条件设置

对于AUV 多传感器组合导航系统而言，惯性组件在实际工作之前已经做了大量的反复试验，其噪声统计特性较为稳定，且精确已知。设置IMU 更新频率为100 Hz，陀螺仪常值漂移误差为0.02 (°)/h，角度随 机游走系数为0.01 (°/h)·Hz0.5；加速度计常值漂移误差为100 μg，速度随机游走系数为10 (μg/Hz)0.5。其他传感器的更新频率一般低于IMU 更新频率，且异步，设置DVL 更新频率为2 Hz，量测噪声为幅值0.1 m/s 的高斯白噪声；TAN 更新频率为0.2 Hz，量测噪声为幅值10 m 的高斯白噪声；MCP 更新频率为1 Hz，量测噪声为幅值5°的高斯白噪声。

由于AUV 各导航传感器在复杂水下环境存在区域性和阶段性的特点，如DVL 因其声学工作环境及回波信号的特殊性易发生短时失效或间歇性失效的情况，MCP 精度不高且易收到环境干扰，TAN 地形匹配定位数据不能大范围覆盖，因此设置各传感器失效区间如下：DVL 失效区间1000～1400 s；TAN 失效区间2000～2600 s；MCP 失效区间700～900 s；SINS 作为一种自主工作的导航系统，抗干扰能力强，因此设置IMU 信息在整个仿真时间段内始终有效。

模拟AUV 在海底作业的三维真实运动轨迹如图3所示，包括直行、转弯等机动动作，仿真总时长为3000 s。

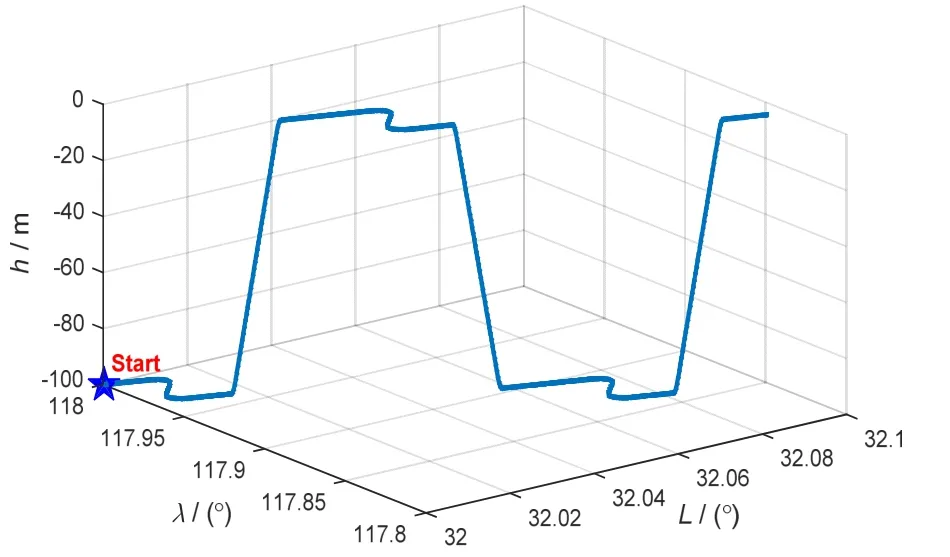
图3 AUV 海底作业运动轨迹 Fig.3 Trajectory of AUV underwater mission

4.2 仿真结果与分析

为了验证本文所提理论方法在传感器信息更新频率异步以及传感器可用性时变情况下的有效性与可靠性，以上述条件为基础对联邦滤波算法和因子图算法分别进行数值仿真实验。

基于因子图方法与联邦滤波方法的AUV 多源信息导航系统仿真结果如图4～6 所示，红线表示因子图方法的仿真结果，蓝线表示联邦滤波方法的仿真结果。

由图4～6 可以看出，在整个仿真时间段内因子图方法与联邦卡尔曼滤波方法始终都能保持输出相对较高精度的导航结果，各导航参数误差都能保持较好的稳定性，其中，姿态角误差在-20′～+20′以内，水平速度误差在-0.1～+0.1 m/s 以内，水平定位误差在-5～+5 m以内，验证了本文所提方法的有效性与可靠性。在传感器可用性动态改变时，由于可利用的信息源减少， 与其他时间段相比，两者的导航精度都会有所降低，与本文第3 节分析一致。

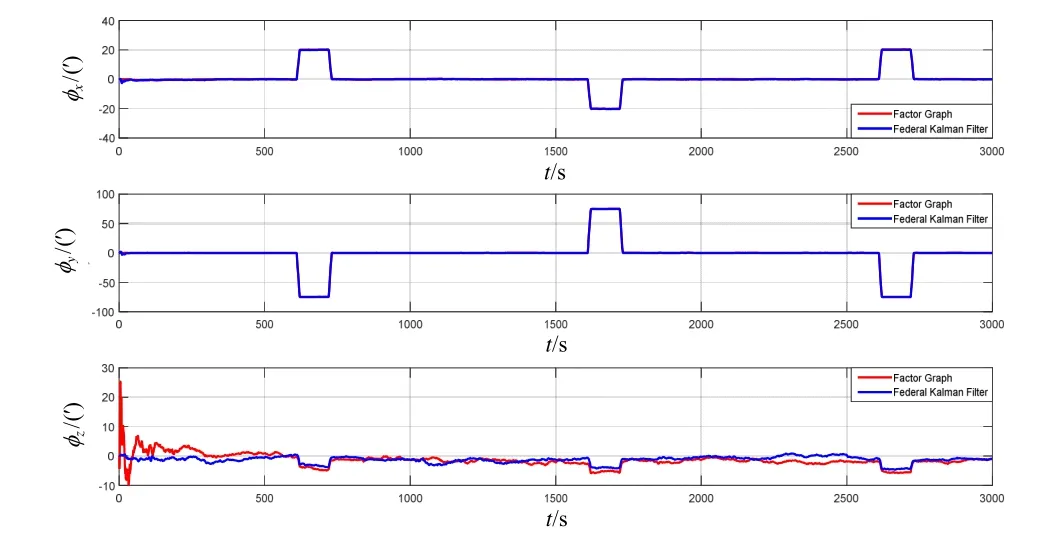
图4 因子图方法与联邦滤波方法的姿态误差角对比曲线 Fig.4 Comparison on attitude errors between factor graph and federal filter method

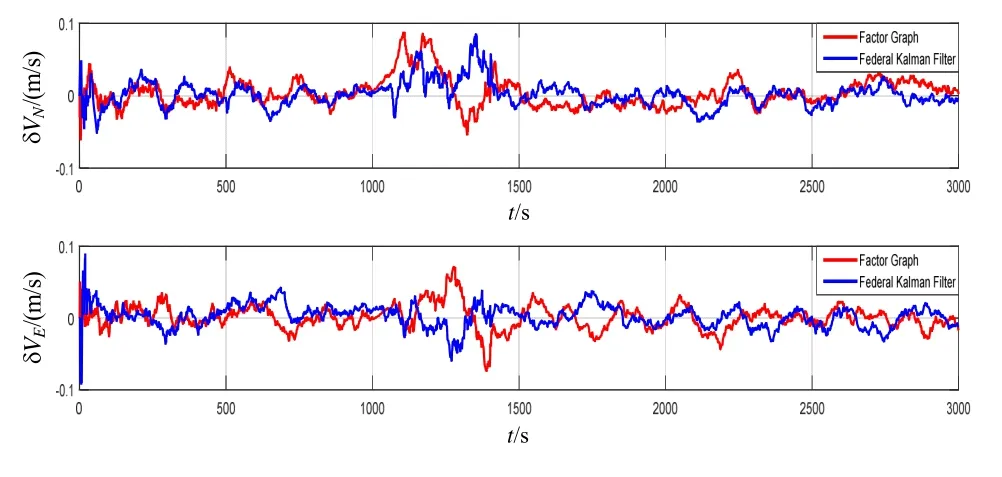
图5 因子图方法与联邦滤波方法的速度误差对比曲线 Fig.5 Comparison on velocity errors between factor graph and federal filter method

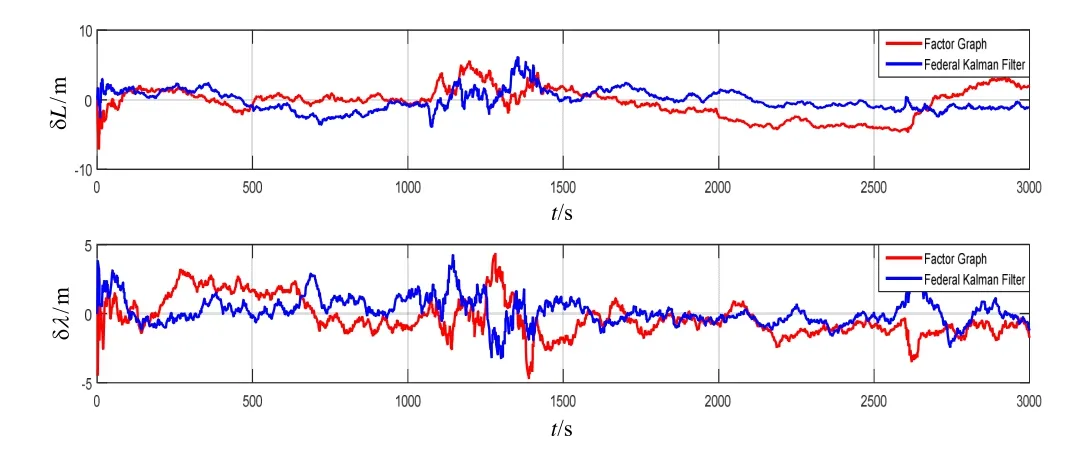
图6 因子图方法与联邦滤波方法的位置误差对比曲线 Fig.6 Comparison on position errors between factor graph and federal filter method

为了定量地分析各导航参数误差，分别计算因子图方法与联邦滤波方法的各导航参数的绝对误差平均值（Absolute Mean Error,AME）与均方根误差值（Root Mean Square Error,RMSE）如表1所示。

从表1可以看出，因子图方法的导航精度与联邦卡尔曼滤波方法相当，基本处于同一水平，与从曲线中得出的结论一致。在表1中，纬度与经度、北向速度与东向速度均属于直接观测量，因子图法能够克服异步影响，及时将观测量引入网络中，因而精度稍高。横滚与俯仰两者均属于间接观测量，两者精度相当；但与航向相比，因航向属于直接观测量，因子图法能够及时将观测量引入滤波网络，因而精度稍高。

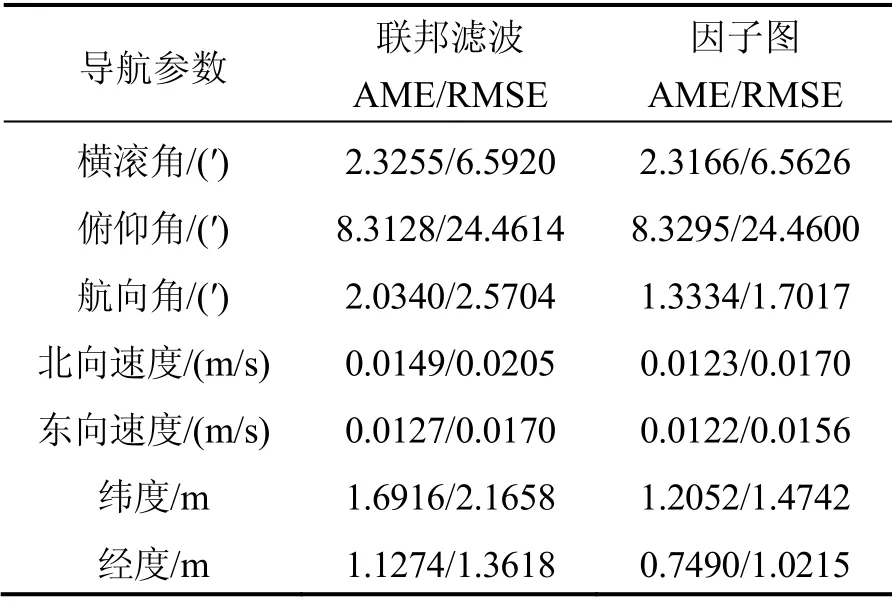
表1 因子图方法与联邦滤波方法的各导航参数 平均误差值与均方根误差值 Tab.1 AME and RMSE of navigation parameters of the factor graph and the federal filter methods

4.3 半物理车载实验

为了验证本文所述基于因子图的AUV 多传感器组合导航算法在实际工程应用中的有效性与可靠性，利用跑车试验对其进行验证。以法国IXBLUE 公司研制的PHINS 和NovAtel 公司研制的FlexPark6 接收机进行SINS/GNSS 松组合所提供的姿态、速度、位置信息作为导航参考数据，输出频率为200 Hz。在其航向角的基础上增加幅值为5°的高斯白噪声来模拟MCP量测数据，采样时间间隔为0.1 s。利用其姿态角和速度得到PHINS 在载体坐标系下的速度，在此基础上增加幅值为0.1 m/s 的高斯白噪声来模拟DVL 量测数据，采样时间间隔为0.3 s。在其位置信息的基础上增加10 m 的高斯白噪声来模拟TAN 量测数据，采样时间间隔为7 s。

图7～9所示为基于本文所提方法的AUV多传感器组合导航跑车试验误差结果。由图7～9 可知，经过车载试验验证，基于因子图的AUV 多传感器组合导航算法能够提供准确的导航信息，各导航参数误差均保持在较小的范围内，水平定位误差在-10～+10 m 以内。基于因子图的AUV 多传感器组合导航跑车试验各导航参数平均误差值与均方根误差值如表2所示。根据表2中的统计结果，亦可得到类似表1及4.2 节的结论。

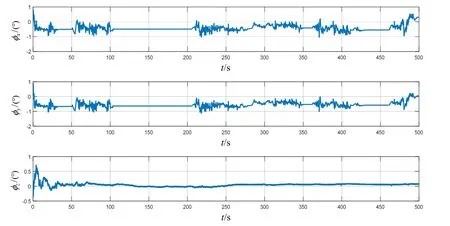
图7 AUV 多传感器组合导航跑车试验姿态角误差 Fig.7 Attitude errors of AUV multi-sensor integrated navigation in vehicle test

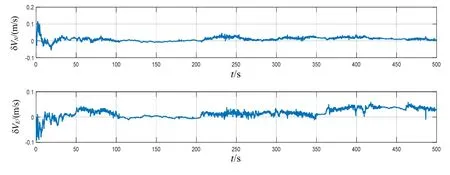
图8 AUV 多传感器组合导航跑车试验速度误差 Fig.8 Velocity errors of AUV multi-sensor integrated navigation in vehicle test

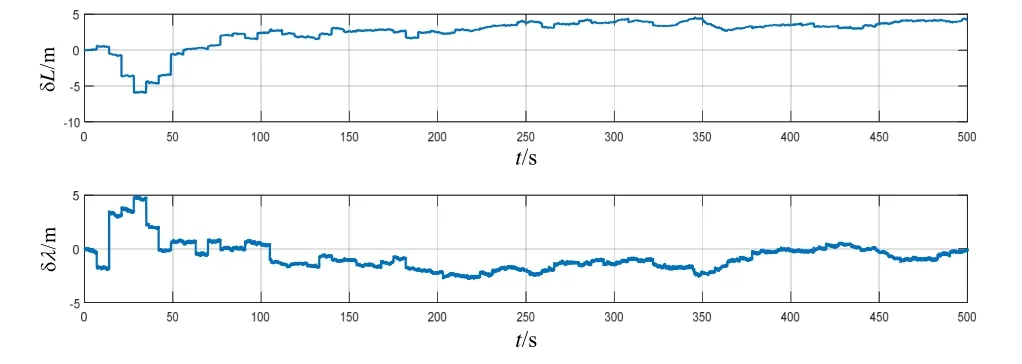
图9 AUV 多传感器组合导航跑车试验位置误差 Fig.9 Position errors of AUV multi-sensor integrated navigation in vehicle test

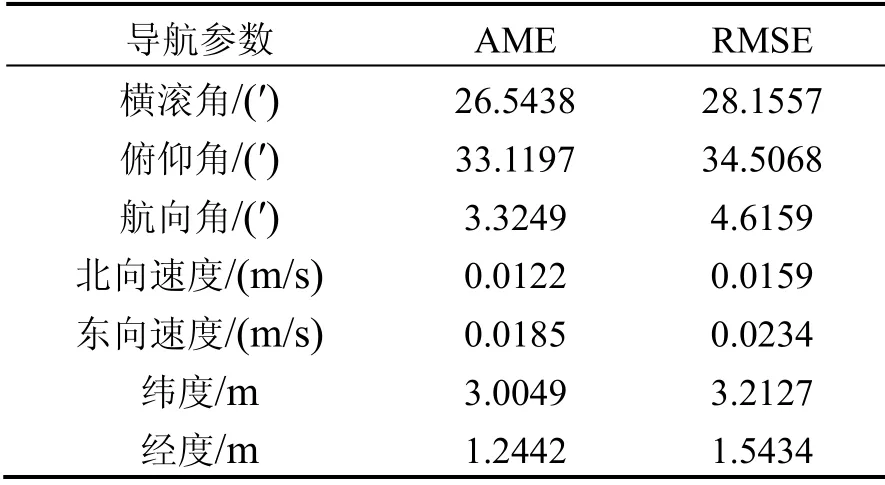
表2 AUV 多传感器组合导航跑车试验各导航参数平均误差值与均方根误差值 Tab.2 AME and RMSE of navigation parameters of AUV multi-sensor integrated navigation in vehicle test

5 结 论

本文提出了基于因子图的AUV 多传感器组合导航算法，实现了SINS/DVL/TAN/MCP 水下组合导航系统的信息融合。该方法将导航状态误差量抽象成变量节点，各导航传感器的量测信息抽象成因子节点，根据非线性优化理论实现变量节点的递推与更新。仿真结果表明，基于因子图的AUV 多传感器组合导航算法能够连续稳定地输出较高精度的导航结果，有效解决惯性导航系统与不同导航传感器的非等间隔融合与传感器可用性动态改变问题，与联邦卡尔曼滤波算法的导航解算精度在同一水平上，但本文所提的因子图方法具有更好的灵活性和扩展性。半物理实验表明，在实际工作系统中，本文所提方案具有较高的可靠性和有效性。