基于灰狼算法的干式双离合器摩擦片优化设计

生浩岩， 安迪， 廉哲满

( 延边大学 工学院， 吉林 延吉 133002 )

双离合器自动变速器(dual clutch transmission，DCT)不仅具有质量轻、结构紧凑、传递效率高的特点，还集合了液力机械式自动变速器以及无极变速器的优点，在不间断动力的情况下能够完成平稳换挡，因而大大提升了车辆的乘坐舒适性以及可操作性，成为近年来主流变速器型式之一[1].然而，DCT因自身冷却能力较弱，使其在大功率输入的情况下，离合器系统的温度会急剧上升，并达到热容极限，进而导致摩擦片表面出现裂纹、永久变形等不良效果，降低其使用寿命.为了改善DCT的不足，学者们对此进行了研究.吴国宽等[2]通过增加冷却途径等方式有效地降低了离合器的温度.杨昭[3]通过改变离合器换挡控制改善了传动系统的综合控制.卜玉帅[4]研究了如何通过调整节气门开度降低离合器的温升.但在相关研究中，未发现有学者通过对摩擦片进行优化来降低温升.鉴于此，本文以某一轿车干式双离合器摩擦片为设计对象，对其5个设计变量进行优化，以摩擦片表面热流密度最小为设计目标，通过Matlab仿真和灰狼优化算法对摩擦片进行优化.

1 干式双离合器工作原理

干式双离合器由两个轴向并联的干式离合器K1和K2组成,如图1所示.离合器K1由压盘Ⅰ、膜片弹簧Ⅰ、离合器盖Ⅰ、从动盘总成Ⅰ组成，离合器K2由压盘Ⅱ、膜片弹簧Ⅱ、离合器盖Ⅱ、从动盘总成Ⅱ组成.干式双离合器的中间驱动盘通过螺栓与发动机飞轮连接；压盘Ⅰ通过传动片与中间驱动盘相连，离合器盖Ⅰ通过螺栓与压盘Ⅰ相连；离合器盖Ⅱ通过螺栓与中间驱动盘相连，压盘Ⅱ通过传动片与离合器盖Ⅱ相连；带有摩擦片的从动盘总成Ⅰ和从动盘总成Ⅱ分别借助其花键毂与变速器输入轴相连.离合器工作时，膜片弹簧通过压盘将从动盘总成压在中间驱动盘上，发动机的转矩由中间驱动盘与从动盘总成和压盘接触面之间的摩擦作用传到从动盘总成上，并最终经变速器的输入轴传到变速箱.

图1 干式双离合器的结构简图

2 优化设计

2.1 优化设计变量

在摩擦片工作状态下，本文将能够产生热流的5项参数确定为设计变量，分别为内径d、 外径D、 摩擦片承受的单位压紧力P0、 摩擦片摩擦系数μ、 储备系数β.

2.2 目标函数的确定

离合器开始工作后，主动盘与从动盘逐渐接触并达到完全结合.这一过程中在摩擦力矩的作用下，摩擦片表面产生大量的热流，使摩擦片的温度迅速上升[3]，即导致离合器温度迅速升高的主要因素是由滑磨产生的热流所引起.由于主动盘与从动盘从逐渐接触到完全结合的滑磨过程时间较短，因此在该过程中可忽略对流换热和热辐射.根据以上分析，本文将摩擦片在滑磨过程中产生的热流密度最小作为目标函数[5]，即：

F(x)=minq=min(μp0ΔωRc).

(1)

式中q为滑磨过程产生的热流密度,μ为离合器摩擦系数，Rc为摩擦片有效半径，P0为摩擦片表面压强，ω为主从动盘间的转速差.在计算过程中，假定摩擦系数、有效半径和压紧力为常数，不考虑温度对这些常数的影响.

2.3 约束条件的确定

1) 摩擦片外径D的最大圆周速度VD不超过70 m/s，即

(2)

式中Nemax为发动机的最高转速(r/min).

2) 摩擦片单位面积的摩擦转矩Tco不能大于材料的许用单位面积摩擦转矩,即

(3)

式中Temax为发动机输出的最大转矩(N·m)，n为摩擦面面数.本文所用的离合器摩擦片材料为粉末冶金铜基，其许用单位面积摩擦转矩[Tco]=0.006 0 N·m/mm2,

3) 摩擦片的单位压紧力P0不能大于材料的许用单位压紧力.粉末冶金铜基的许用单位压紧力[P0]为0.35～0.5 MPa，因此本文取

(4)

式中F0为摩擦片所受的压紧力.

4) 摩擦片外径D在175～420 mm范围内[6].

5) 摩擦片内径d在125～210 mm范围内[6].

6) 摩擦片内外径之比c在0.53～0.77范围内[6].

7) 摩擦片摩擦系数μ确定为0.25～0.35[7].

8)工作储备系数β过小会影响离合器传递转矩的可靠性，而β过大则会增加离合器的尺寸和重量.根据干式双离合器的特点，取β为1.2～3[8].

3 灰狼优化算法分析

3.1 灰狼优化算法原理

灰狼优化算法(grey wolf optimization，GWO)[9]是由Mirjalili等于2014年提出的一种新型的群体智能优化算法.它是通过模拟灰狼群体的等级机制和在自然界中的捕食行为来实现求解优化问题的目的.由于该算法具有所需参数少且能快速收敛的优点，因此被广泛应用于电力系统[10]和无人机路径规划等领域中[11].图2为灰狼优化算法的主要运算过程.经试验表明，灰狼个数N<6时，迭代次数过多，且优化效果不好；N>6时，易出现罚值：因此，本文取灰狼个数N=6.本文取最大迭代次数tmax=500代，因为在该迭代次数下，迭代曲线和优化效果均较为理想.

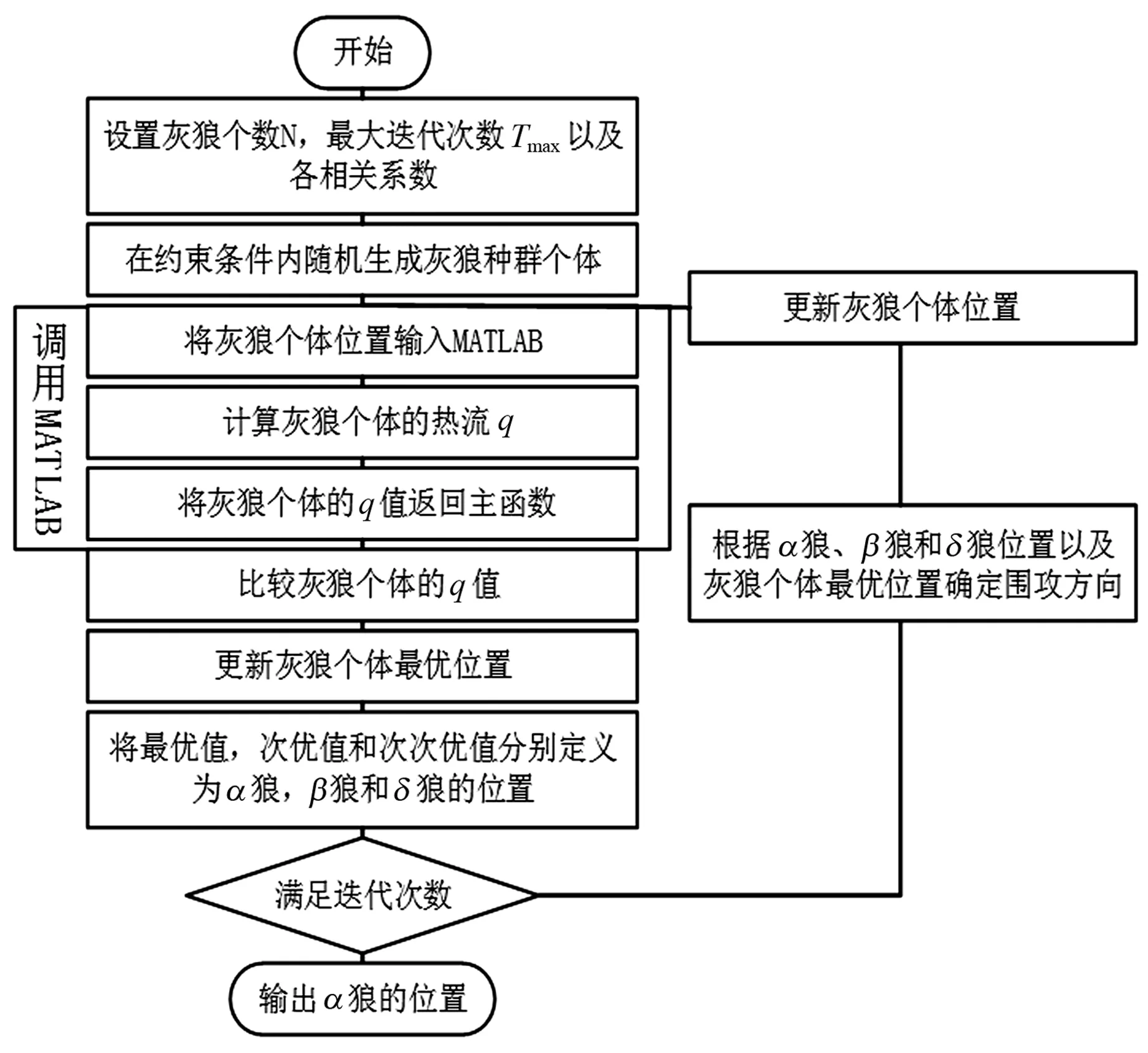
图2 灰狼算法优化流程图

3.2 优化结果

轿车的相关固定参数如下：发动机最大输出转矩Temax=246 N·m，发动机的最高转速Nemax=6 500 r/min.由于干式双离合器一般为双片摩擦片，所以摩擦面面数为2.转速差ω的表达式为

式中t为滑磨时间(s).由上式可知，转速差最大的时间点为t=0.5 s.为了节省运算时间，本文将转速差设置为该时间点的值，并求解该时间点热流密度的最优解.

根据上文建立的数学模型，对离合器进行以摩擦片表面热流密度最小为目标的灰狼算法优化设计.图3为灰狼优化算法的最优值迭代曲线图.由图3可知，随着迭代次数的增加迭代结果逐渐下降，并在约270代处曲线趋近平稳,说明优化得到了最优解.由表1优化前后的各参数值可知，经过灰狼算法优化设计后，摩擦片表面热流密度在t= 0.5 s时为14 113.346 J/(m2·s)，比优化前的热流密度减少了14.03%.算法中各项约束条件输出的惩罚值均为0，表明求得的结果符合设计条件.以上结果表明，本文的总体优化结果较为理想.

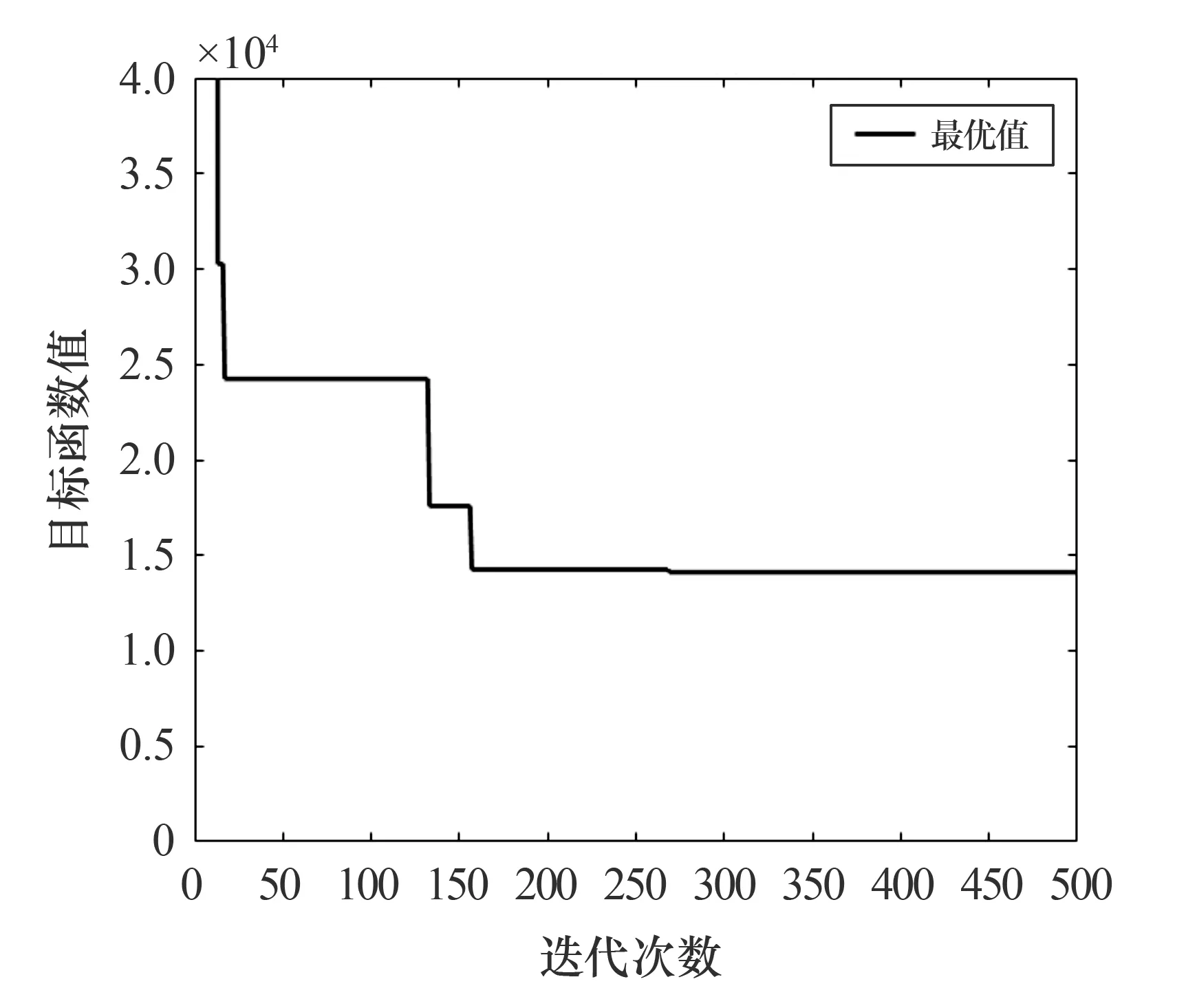
图3 灰狼算法优化的迭代曲线

设计参数优化前参数优化后参数外径D/mm225205.564内径d/mm150124.860内外径比c0.670.607摩擦系数μ0.320.25工作储备系数β1.31.2摩擦片所受压紧力F0/MPa5225.57005.5单位压紧力P0/MPa0.270.335热流密度q/(J/(m2·s))1641614113.346

4 结论

本文对干式双离合器摩擦片的5个相关设计变量进行参数优化，并采用Matlab灰狼优化算法对摩擦片表面热流密度进行了优化设计.结果表明，优化后摩擦片的表面热流密度比优化前减小了14.03%(在t=0.5 s时).因此，本文方法对干式双离合器摩擦片的优化设计具有一定的参考价值.本文在优化过程中,忽略了温度对摩擦系数、压紧力及有效半径的影响.因此，在后续研究中将进一步考虑这些因素对模型的影响，以建立一个更加合理的热流密度优化模型.