求解二阶锥互补问题的一种非精确光滑化牛顿算法

薛文娟

( 福建农林大学 计算机与信息学院, 福建 福州 350002 )

0 引言

定义Rn中的二阶锥(SOC)为:

Kn={(x1,x2)∈R×Rn-1|x1≥‖x2‖},

不失一般性，本文考虑单个二阶锥上的二阶锥规划，其原问题(PSOCP)为:

min{cTx|Ax=b,x∈Kn},

其中A∈Rm×n,c∈Rn,b∈Rm为给定的已知量，x∈Kn为变量.原问题的对偶问题(DSOCP)为:

max{bTy|ATy+t=c,t∈Kn,y∈Rm},

其中t∈Kn为松弛变量，y∈Rm为变量.

二阶锥互补规划问题作为数学领域的一个重要分支，在工程、金融等领域具有广泛地应用[1].2002年，Qi等[2]提出了一种光滑化牛顿法用于求解变分不等式等问题，因为该方法具有较好的收敛性和计算效果，所以被广泛地应用于二阶锥规划问题的求解中[3-7].但目前为止，该方法大多用于求解线性互补问题，而较少应用于锥互补问题的研究；因此，本文基于一个向量函数，给出二阶锥规划问题的一种非精确光滑化牛顿算法，并证明该算法具有全局收敛性.

1 预备知识

(1)

用x2表示x∘x,x+t表示向量加法，于是(∘,+，ε)构成一个若当代数，其中ε=(1,0)∈R×Rn-1.

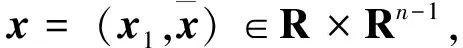
x=λ1u1+λ2u2;

(2)

λi=x1+(-1)i‖x2‖;

(3)

(4)

g(x)=g(λ1)μ1+g(λ2)μ2，x∈Kn.

(5)

由式(5)可得：

[x]+= [λ1]+u1+[λ2]+u2，x∈Rn;

lnx=lnλ1·u1+lnλ2·u2，x∈Kn.

定义一个向量值函数φ∶Rn×Rn×R++→Rn为

(6)

令z∶=(x,t,μ)， 定义函数H(z)∶Rn×Rm×R++→Rm×Rn×R++为

(7)

以下给出φ(x,t,μ)的一些性质.

ii) 对任意z=(x,y,μ)∈Rn×Rm×R++, 函数φ(x,t,μ)均为连续可微，且此函数的雅可比为

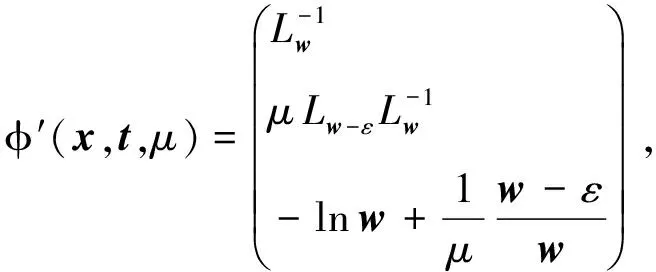
iv)φ(x,t,0)=0 ⟺x∈Kn,t∈Kn,xTt=0.

4)由于Kn={x∈Rn|xTt≥0,∀t∈Kn}是一个闭的自对偶凸锥，则根据文献[8]中的引理2.2可得对任意两个向量x,y∈Rn, 满足x=[x-t]+⟺x∈Kn,t∈Kn,xTt=0.

定理1定义函数H(z)如式(7)，则有如下结论：

i) 问题PSOCP和DSOCP的解与方程组H(z)=0的解一致.

ii) 对任意z=(x,y,μ)∈Rn×Rm×R++，H(z)连续可微，其雅可比为

(8)

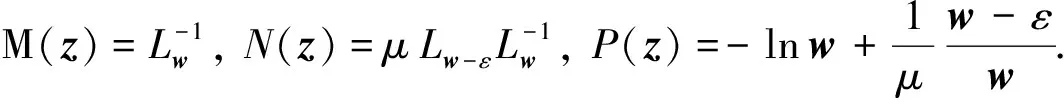
iii)如果矩阵A的行向量组线性独立，则对任意μ>0,H′(z)为非奇异.

证明1)因求解问题PSOCP和DSOCP等价于求解

Ax=b,ATy+t=c,x∘t=0,x∈Kn,t∈Kn,

则由性质1的iv)知问题PSOCP和DSOCP的解与方程组H(z)=0的解一致，结论i)得证.

2)由式(7)和性质1中的φ′(x,t,μ)表达式易得结论ii)成立.

3)为证明结论iii)，令Δz∶=(Δx,Δy,Δμ)∈Rn×Rm×R.在此只要证明方程H′(z)Δz=0只有零解即可.由式(8)知方程H′(z)Δz=0等价于

(9)

2 光滑化牛顿算法及其收敛性

ψ(z)∶=‖H(z)‖2,β(z)∶=rmin{1,ψ(z)}.

第1步 若ψ(zk)∶=‖H(zk)‖2≤ξ, 则停止算法；否则计算

βk∶=β(zk)∶=rmin{1,‖H(zk)‖2}.

(10)

第2步 求解方程(11)得Δzk∶=(Δxk,Δtk,Δμk)∈Rn×Rn×R++.

DH(zk)Δzk=-H(zk)+βk‖H(zk)‖2e0,

(11)

其中DH(zk)为H(z)在点zk处的雅可比表达式.

第3步αk是1,δ,δ2,…中满足条件

ψ(zk+αkΔzk)≤[1-σ(1-rμ0)αk]ψ(zk)

(12)

的最大数.

第4步 令Δzk+1∶=zk+αkΔzk,k∶=k+1; 转到第1步.

定理2设矩阵A行向量线性独立,则算法1可产生无穷序列{zk∶=(xk,tk,μk)}, 且下述结果成立：

i) {ψ(zk)}、{‖H(zk)‖}和{βk}均是单调下降的，且{ψ(zk)}、{‖H(zk)‖}收敛于0.

ii) 记Ω∶={z∶=(x,t,μ)∈Rn×Rn×R++,μ≥μ0β(z)‖H(z)‖2}, 则zk∈Ω.

证明1)由于矩阵A行向量线性独立,则类似文献[9]中的定理3.1的证明，可得算法1是可行的.因此，算法1能产生无穷序列{zk∶=(xk,tk,μk)}.由式(12)可得{ψ(zk)}是单调下降的，因此{‖H(zk)‖}和{βk}均是单调下降的.

2)利用归纳法证明ii).由于β(z0)‖H(z0)‖2=r‖H(z0)‖2min{1,‖H(z0)‖2}≤r‖H(z0)‖2<1, 因此μ0≥μ0β(z0)‖H(z0)‖2, 故z0∈Ω.假设zk∈Ω， 即μk≥μ0βk‖H(zk)‖2, 则

μk+1-μ0βk+1‖H(zk+1)‖2=μk+αkΔμk-μ0βk+1‖H(zk+1)‖2=

μk+αk[-μk+μ0βk‖H(zk)‖2]-μ0βk+1‖H(zk+1)‖2=(1-αk)μk+

αkμ0βk‖H(zk)‖2-μ0βk+1‖H(zk+1)‖2≥(1-αk)μ0βk‖H(zk)‖2+

αkμ0βk‖H(zk)‖2-μ0βk+1‖H(zk+1)‖2=μ0βk‖H(zk)‖2-μ0βk+1‖H(zk+1)‖2=

μ0[βk‖H(zk)‖2-βk+1‖H(zk+1)‖2]≥0.

(13)

式(13)中的第1个不等式可由zk∈Ω得到，第2个等式可由式(10)得到，最后的不等式(≥0)可由结果i)得到.

假设1问题SCCP的解集S∶={(x,t)∈Rn×Rn:x∈Kn,t∈Kn,xTt=0,Ax=b,ATy+t=c} 为非空有界.

定理3设矩阵A行向量线性独立, {zk∶=(xk,tk,μk)}是由算法1得到的无限序列,则{zk∶=(xk,tk,μk)}任一聚点z*=(x*,t*,μ*)是H(z)=0的解.

证明因证明类似于文献[9]中定理3.2的证明，故在此省略证明.

3 数值试验

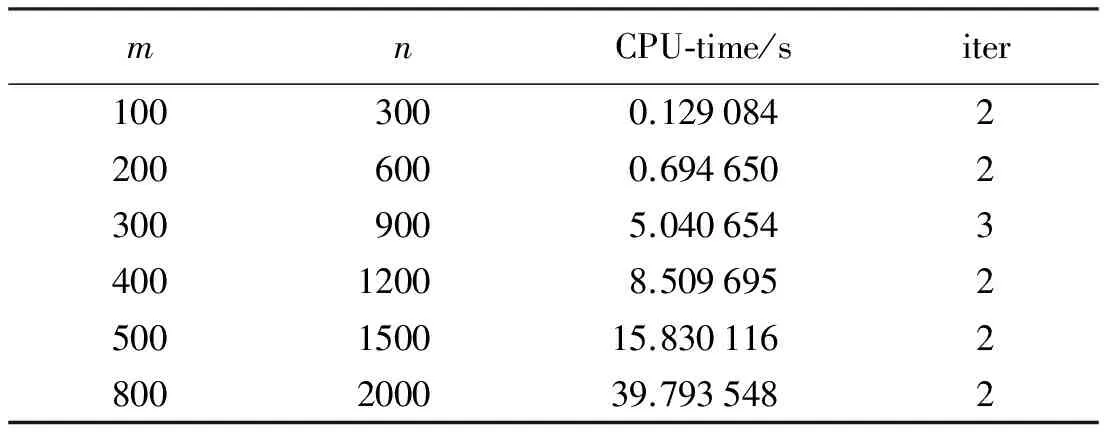
表1 算法1的数值试验结果