离合器压盘热变形与应力分析方法及其应用*

万里翔, 陈 浩,刘雪莱,侯秋丰,于 洋,上官文斌

(1.西南交通大学机械工程学院，成都 610031；2.华南理工大学机械与汽车工程学院，广州 510641；3.宁波宏协离合器有限公司，宁波 315807；4.天津一汽夏利汽车股份有限公司，天津 300380)

2016216

离合器压盘热变形与应力分析方法及其应用*

万里翔1, 陈 浩1,刘雪莱2,侯秋丰3,于 洋4,上官文斌2

(1.西南交通大学机械工程学院，成都 610031；2.华南理工大学机械与汽车工程学院，广州 510641；3.宁波宏协离合器有限公司，宁波 315807；4.天津一汽夏利汽车股份有限公司，天津 300380)

为解决离合器压盘在使用过程中的断裂问题，建立了离合器压盘热变形与应力的分析模型。建模中，考虑了波形片轴向非线性特性和摩擦因数随转速差的变化。利用模型对离合器压盘接合过程中的温度分布进行仿真分析，并通过实测验证模型的正确性。基于分析结果，提出压盘改进方案，并进行装车测试，离合器压盘未出现断裂情况，证明了本文的建模方法与分析过程的正确性。

离合器；压盘；温度场分析；温度测试；热结构耦合

前言

压盘作为离合器总成中的重要部件，在使用过程中会出现烧蚀、变形甚至断裂的现象；而这些现象会导致离合器传递转矩的能力下降，离合器踏板行程增加；更严重的甚至影响到汽车在行驶过程中的安全性。离合器由离合器盖、压盘、摩擦片、压紧与分离机构等组成，其中，离合器盖与压盘和飞轮连接，摩擦片与变速器输入轴相连。在汽车起步过程中，压盘跟随发动机一起转动，摩擦片与压盘逐步接合；通过滑摩传递转矩直至接合完成。在汽车起步过程中，摩擦片与压盘间滑摩产生了大量热量。由于接合时间短，离合器工作环境相对封闭，压盘温度在短时间内快速升高，致使压盘产生热变形与热应力。

一款离合器总成，在装车测试的过程中，压盘由于温升产生的热应力发生了断裂。断裂发生于车辆满载半坡起步工况，离合器处于半联动状态。实车测试过程中有10%的几率导致离合器压盘断裂。为解决该问题，需要研究缺口半径、压盘整体厚度和压盘在离合器接合过程中产生的热应力集中与热变形，并采取措施予以改进，以提高压盘在使用过程中的可靠性。

在离合器传递转矩与传热方面的研究如下。文献[1]和文献[2]中综合考虑了波形片与膜片弹簧的轴向非线性特性，摩擦因数与转速差变化关系，建立了离合器传递转矩的数学模型。文献[3]中在此模型的基础上推导出离合器接合过程中，产生滑摩功的数学模型，并对离合器表面温度进行仿真分析。文献[4]～文献[6]中推导了离合器接合过程中产生的滑摩功，利用有限元方法对离合器摩擦副进行温度分析，结果表明，压紧力分布、压盘厚度和滑摩功的大小对压盘滑摩表面的温度有重要的影响。文献[7]中提出通过用电容等效压盘和飞轮上的热容量，用电阻来等效离合器系统中的热对流和热交换，从而计算压盘温度，并进行了相关试验，结果表明：该模型能较好地预测压盘温升情况。文献[8]中利用温度测量系统对摩擦副接合时的温度进行了测量，得出了因温度升高而产生的热应力是压盘变形失效的主要因素的结论。文献[9]中对压盘在接合过程中的温度和转矩传递进行了试验分析，结果表明：压盘因为受热而产生的变形会导致离合器传递转矩能力的下降。

上述研究工作主要是对压盘在滑摩过程中温度场的分布情况做出分析与预测，更多的是通过理论上的分析，大都未经试验验证。同时，虽然很多文献也提到压盘受热产生的应力与变形对压盘失效产生影响，但是并没有提出有针对性的改进措施。

本文中基于某款离合器压盘在装车测试的过程中出现缺口处断裂的问题，对该款压盘进行了热应力与热变形分析。首先，在考虑波形片非线性特性以及摩擦因数在滑摩过程中变化的基础上，建立了离合器传递转矩的模型，计算了接合过程中产生的滑摩功。然后，用有限元方法对压盘进行温度场分析，并通过试验验证模型的正确性。再将温度作为载荷导入到结构分析中，计算得到了压盘受热产生的热变形和热应力。结果表明：计算出的压盘应力最大位置与断裂位置一致。接着对压盘进行结构改进，并经计算发现，随着压盘缺口半径增大而变浅，缺口下缘应力减小；而压盘加厚后，缺口上缘应力减小。最后提出了压盘改进方案，进行装车测试，在测试过程中，离合器运行良好，未出现压盘断裂情况。本文中的建模和分析方法对离合器压盘的设计与开发具有指导意义。

1 压盘温度场分析

1.1 压盘温度场测试方法

离合器压盘温度场测试旨在了解离合器压盘在汽车起步过程中的温度场分布及变化趋势，该测试在离合器综合性能试验台上进行。试验台的结构如图1所示。

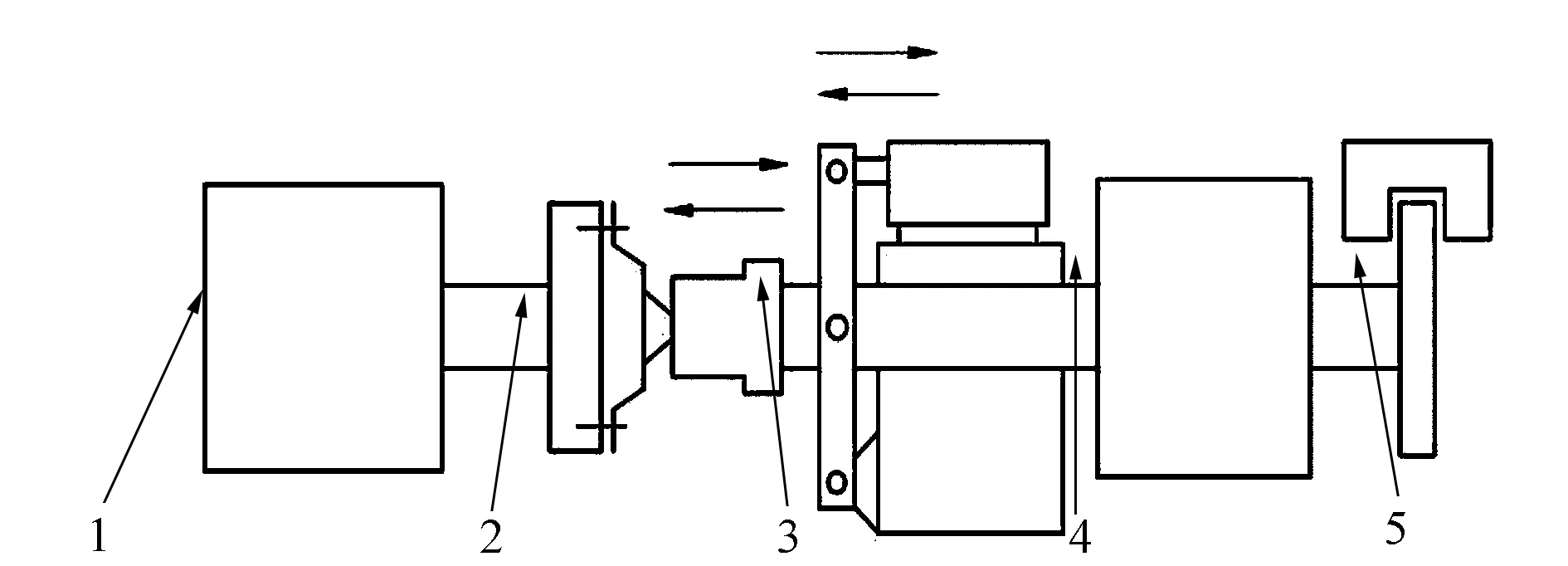
1—电机模块；2—离合器安装模块；3—离合器分离接合控制模块4—试验台惯量模块;5—试验台制动模块图1 离合器综合性能试验台结构原理示意图

在图1中，电机模块为整个试验台提供动力，模拟汽车发动机转速转矩。离合器安装模块用来安装离合器总成。压盘控制模块在试验台运行时，模拟分离轴承，依靠气泵的前进与后退，控制离合器压盘与摩擦片的分离与接合。试验台惯量模块用来模拟汽车行驶过程中的整车惯量。试验台制动模块在试验台试验结束时对传动轴进行制动。

测试时，从压盘的支撑面打螺纹孔，孔底距离滑摩表面3mm，三孔之间的圆周间距为120°。在螺纹孔中拧入热电偶。在测试过程中，热电偶采集到的数据将通过蓝牙进行传输。将带有热电偶的离合器总成安装到试验台上的离合器安装模块上，分离机构推动气泵前进，使离合器压盘与从动盘处于分离状态。电机稳定在730r/min的设定转速，计时器开始计时，气泵推动离合器接合，滑摩开始。当主、从动盘转速达到一致时，立刻分离。温度传感器记录压盘在整个循环中的最高温度，当计时达到30s时气泵再次接合，开始进行下一个循环。连续进行5次循环，记录温度传感器数据。

1.2 滑摩功与滑摩功率的计算

离合器接合过程中，所传递的转矩[10]为

(1)

式中：Tc为离合器传递的转矩；μ为离合器摩擦面滑动摩擦因数；Fc为离合器压紧力；R0为压盘滑摩面外径；R1为压盘滑摩面内径。在建模过程中仅考虑压盘与摩擦片之间的转速差ω对摩擦因数的影响[10]，即

μ(ω)=μd+(μs-μd)e-ω

(2)

式中：μs为最大静摩擦因数；μd为滑动摩擦因数，可由试验数据拟合得到。

由文献[2]中试验可知，在离合器接合的过程中，分离轴承的位移与摩擦片中波形片的变形量近似成正比，此时，膜片弹簧在此过程中产生的压紧力不起决定性作用。因此，在接合过程中，只认为压盘受到的压紧力与波形片的非线性压缩特性有关。图2为试验得到的离合器总成波形片的面压缩特性曲线，通过对试验数据的拟合得到压紧力模型。

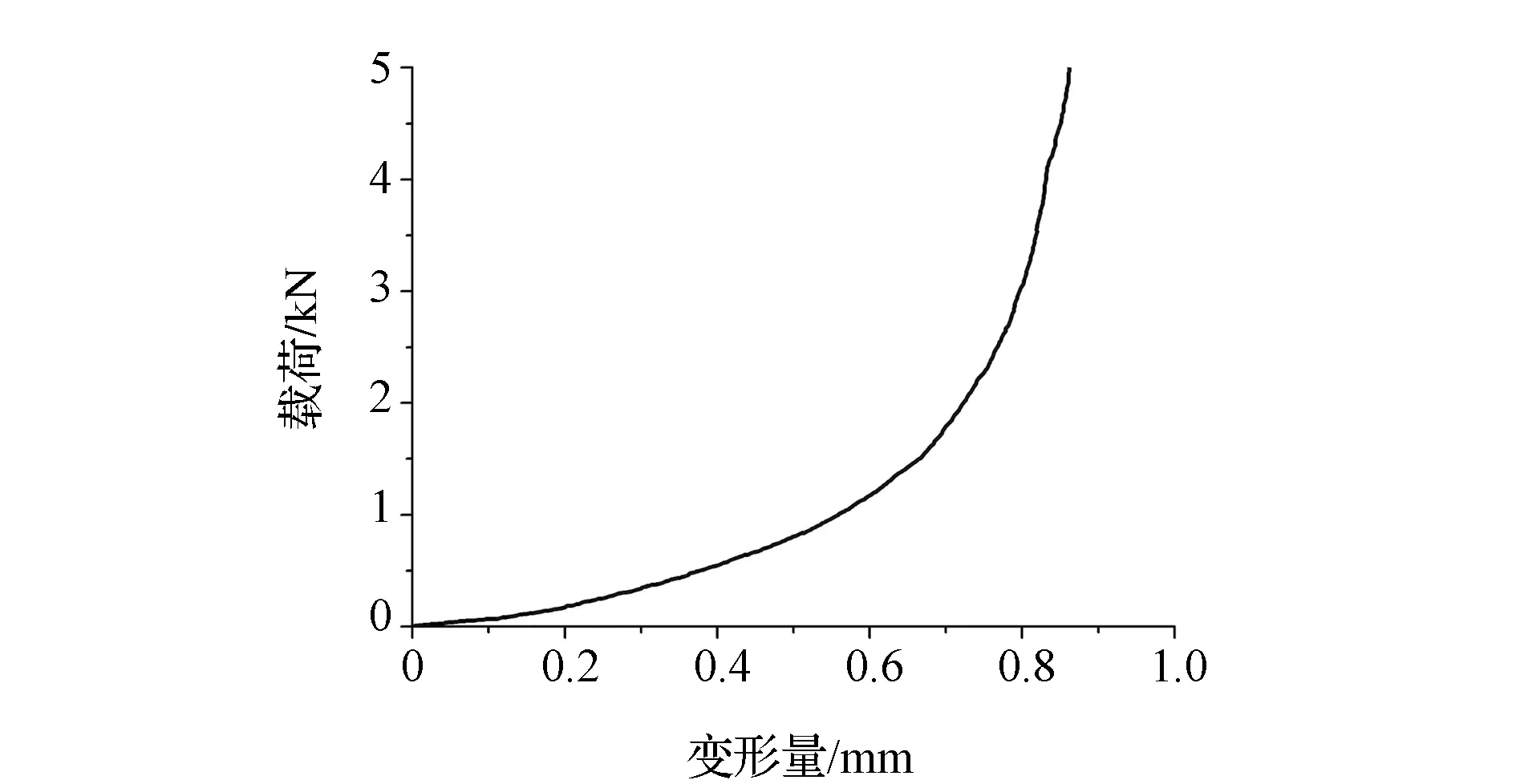
图2 波形片面压缩特性曲线

离合器压紧力Fc与摩擦片波形片变形量x的关系为

Fc=Ax5+Bx4+Cx3+Dx2+Ex

(3)

式中：A，B，C，D和E为拟合参数。

离合器接合过程中，离合器压盘与摩擦片之间由于速度差产生滑摩，在滑摩过程中消耗大量能量，这部分能量称为滑摩功，滑摩功和滑摩功率分别为

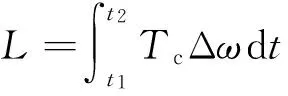
(4)

式中：L为滑摩功；P为滑摩功率；t1为开始接合时刻；t2为压盘、摩擦片转速相同时刻；Δω为压盘与摩擦片间的角速度差。

式(4)所得的计算结果如图3所示。由图可见，一次接合压盘产生的滑摩功约为8kJ，滑摩功率峰值约为7.4kW。

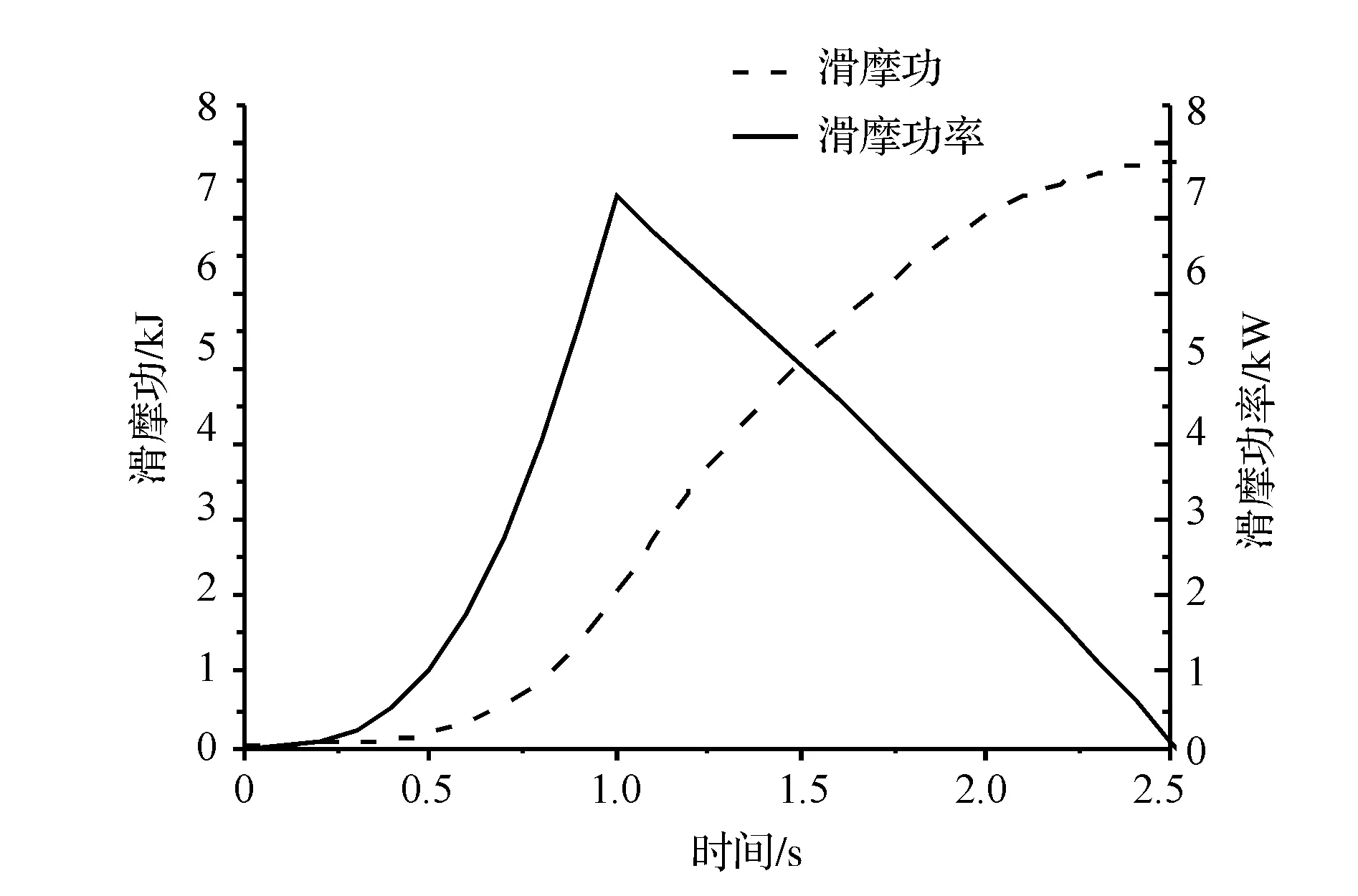
图3 滑摩功与滑摩功率曲线

1.3 温度场计算模型与边界条件

离合器温度场测试过程中，离合器接合时压盘与摩擦片发生滑摩，产生热量，热量传递到压盘。压盘温度场计算即是利用有限元软件模拟这一过程中压盘与摩擦片接触表面的温度变化。模拟手段为在压盘与摩擦片接触面上施加热流密度，即温度载荷。

通过滑摩功率可推导出热流密度，摩擦片某一点上产生的滑摩功率与热流密度间的关系为[11]

(5)

式中：q(t)为热流密度；R为压盘所研究点的半径；N(t)为滑摩功率。

离合器在接合过程中，滑摩表面吸收摩擦产生的热量，其它表面存在与空气的对流换热，同时向四周发出热辐射。分离时，压盘所有表面存在与空气的对流换热，并向四周发出热辐射。因此，本文中所建立的有限元模型将热辐射对流换热等因素作为边界条件考虑在内。

物体总是在不停地对外辐射和吸收能量。在传热学中，为便于研究，定义黑体为一种理想模型，可以用它作为衡量其他表面辐射能力的参照基准。物体实际对外辐射能力与对应的黑体辐射能力的比值称为辐射率，以ε表示：

ε=E/Eb

(6)

式中：E为实际物体辐射力；Eb为黑体辐射力。

物体的辐射率取决于物质种类、表面温度和表面形状，故物体辐射力为

E=εσT4

(7)

式中：σ为黑体辐射系数，σ=5.67×10-8。

压盘在接合过程中，散热主要依靠与周围的空气进行对流换热。而对流换热系数随着压盘的转速和周围温度不断变化，很难确定。本文中采用盘式对流换热系数经验公式：

(8)

其中Re=vL/vν

(9)

式中：λa为空气导热系数；d为压盘直径；Re为雷诺数；v为空气流速(本文中取压盘中径线速度，随时间变化)；L为压盘中径；ν为空气的运动黏度。

压盘和摩擦片在滑摩过程中既产生热量，又吸收热量。压盘与摩擦片吸收热量的比值，可通过热流分配系数K得到，其计算公式为

(10)

式中：λ1为摩擦片导热系数；λ2为压盘导热系数；c1为摩擦片比热容；c2为压盘比热容；ρ1为摩擦片密度；ρ2为压盘密度。式(8)～式(10)中参数数值见表1。

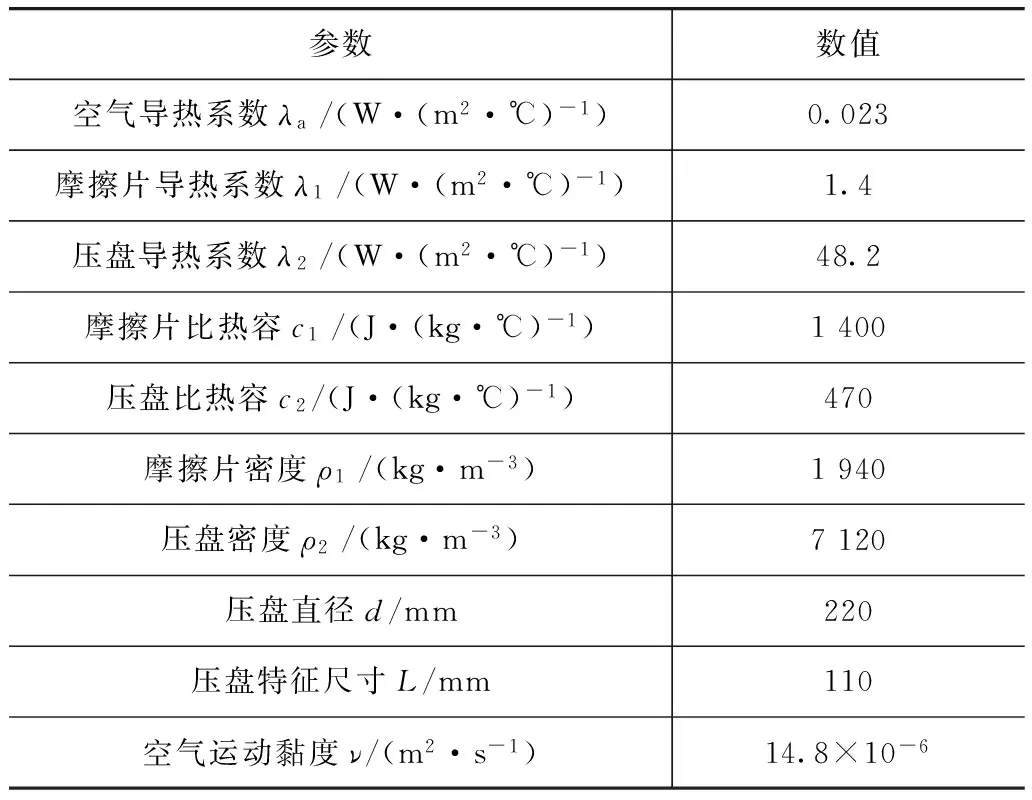
表1 模型计算参数

本文中使用的压盘材料为HT250，摩擦片以铜基合金粉末为基体材料。

1.4 温度场计算结果

建立离合器压盘三维模型，导入有限元软件中并建立有限元模型进行温度场计算。

图4 温度场峰值时刻温度分布图

图4为压盘温度场峰值时刻的温度云图。在1.8s时，压盘最高温度达到52.9℃，出现在滑摩表面的外缘处，高温区主要集中在滑摩表面。由于此时离合器从动盘与飞轮处于滑摩阶段，且由式(5)可知，滑摩表面的热流密度与半径成正比，这与温度最高点出现在滑摩表面外缘处的实际情况相符。压盘的支撑面由于接合时间短，热量还未得到及时传导，因此温度未有明显变化。

图5为温度循环结束时压盘温度场分布。在30s时，从动盘与飞轮的滑摩过程已经结束，且转速增高导致热对流带走的能量增加，使温度整体下降到39.1℃。但是滑摩表面的温度分布趋势没有变化。部分热量已经传递到压盘的支撑面上，因此，温度也有所升高。压盘定位孔处在离合器运转过程中不与热源直接接触且线速度最大，因此热量流失现象明显，温度没有明显变化。

图5 温度循环结束时刻温度分布图

图6为温度场仿真计算与试验结果对比。

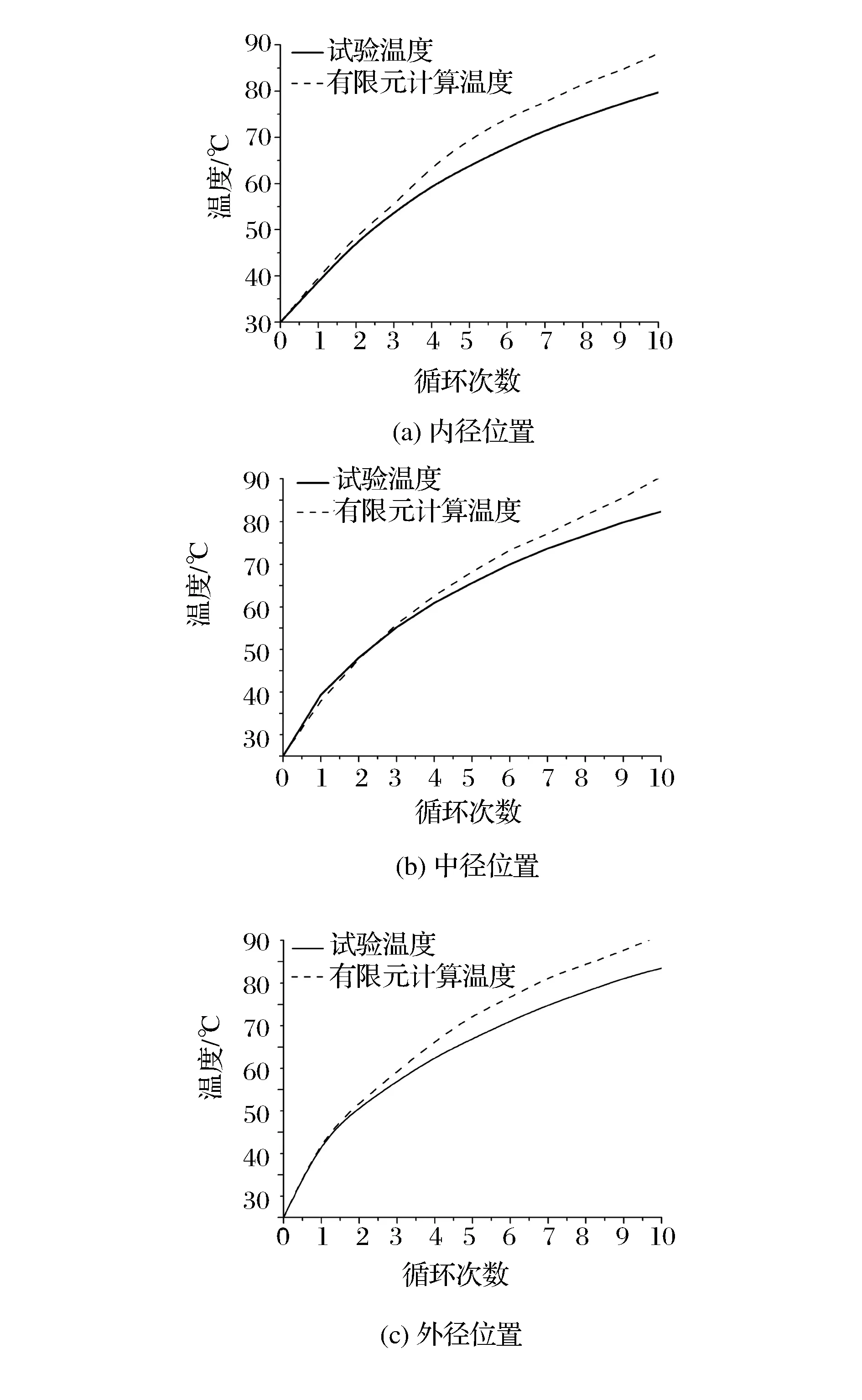
图6 压盘内、中、外径位置温度的试验值与计算值对比

由图可见，温度场测试结果与仿真结果变化趋势相同，很好地验证了本文中建立的压盘温度场有限元模型的正确性。但随着循环次数的增加，试验值和计算值的偏差加大。这是由于压盘比热容会随着温度升高而增大，随着循环次数增加，吸收相同热量，压盘的温升值会降低。对流换热系数也会随温度变化而变化。

对比试验与仿真结果，内、外径仿真温度随着循环次数的增加，计算温度值高于试验值，中径温度与试验结果误差较小。其主要原因是：

(1)内径和外径边缘处打孔安装温度传感器，对流换热情况复杂；

(2)由于压盘产生的热变形，可能导致滑摩表面热流密度分布情况改变；

(3)随着温度的升高，压盘本身的比热容也会变化，但是在仿真的过程中并未考虑；

(4)温度传感器通过在压盘上钻孔安装，且温度测量位置与压盘滑摩表面距离3mm，但是现实中安装会有一定误差。

2 压盘热应力与变形分析

2.1 汽车起步过程动力学模型

离合器压盘是在汽车起步过程中出现断裂现象，因此，需要对压盘在真实工作工况下的情况进行仿真分析。本文中模拟汽车以恒定的节气门开度(10%)，在12%的坡道上满载起步的工况。

发动机输出转矩是发动机节气门开度和发动机转速的函数：

Te=f(α,ne)

(11)

式中：Te为发动机输出转矩；α为节气门开度；ne为发动机转速。

在节气门开度一定的情况下，发动机输出转矩曲线可由试验数据三次样条插值拟合达到满意的精度[12]，可用一定数量的试验数据建立发动机输出转矩的输出模型。根据发动机的试验数据及其应用范围, 绘制出发动机不同节气门开度和转速时的发动机输出转矩曲线。

汽车起步时，离合器接合过程可分为3个阶段。

(1) 第一阶段：离合器主、从动盘开始接合，但此时离合器传递的转矩小于汽车起步的阻力矩，从动盘角速度ωc=0，车辆静止不动，则

(12)

(2) 第二阶段：随着压盘压紧力的增加，离合器所传递的滑摩转矩逐渐大于汽车起步行驶阻力矩，发动机转速降低，汽车开始起步，则

(13)

(3) 第三阶段：离合器主、从动盘之间转速达到一致，不再有滑摩，离合器完全接合。从动盘传递的转矩等于发动机的输出转矩，则

(14)

式中：Je为发动机旋转部分和离合器主动盘的转动惯量；Jc为离合器从动盘带动所有转动部件和整车转换到离合器从动盘上的转动惯量；Te为发动机输出转矩；Tc为离合器传递转矩；Tf为外界阻力矩换算在变速器输入轴上的当量阻力矩；ωe为发动机输出轴角速度；ωc为离合器从动盘角速度[12]。

作用在变速器输入轴上的当量阻力矩为

Tf=[(f+sinαi)mvg+CDAu2/21.15]rw/(i0ig1η)

(15)

式中：mv为汽车的整备质量；u为车速；CD为空气阻力系数；A为迎风面积；rw为车轮半径；αi为道路坡度；f为滚动阻力系数；i0为主减速器传动比；ig1为变速器1挡传动比；η为传动效率。

2.2 计算结果及其分析

在模拟汽车起步的工况中，节气门开度保持恒定，由式(11)可知，发动机输出转矩可以通过转速计算得到；将12%坡度的数据代入式(15)中，可以计算出作用在变速器输入轴上的当量阻力矩。依据上第2.1节中所建立的汽车起步的动力学模型，由式(4)可算得汽车在起步工况下离合器接合的滑摩功和滑摩功率，通过式(5)计算得到接合产生的热流密度，利用有限元方法对压盘进行温度场计算，边界条件的确定方法与第1.3节中的方法相同。分析结果如图7所示。

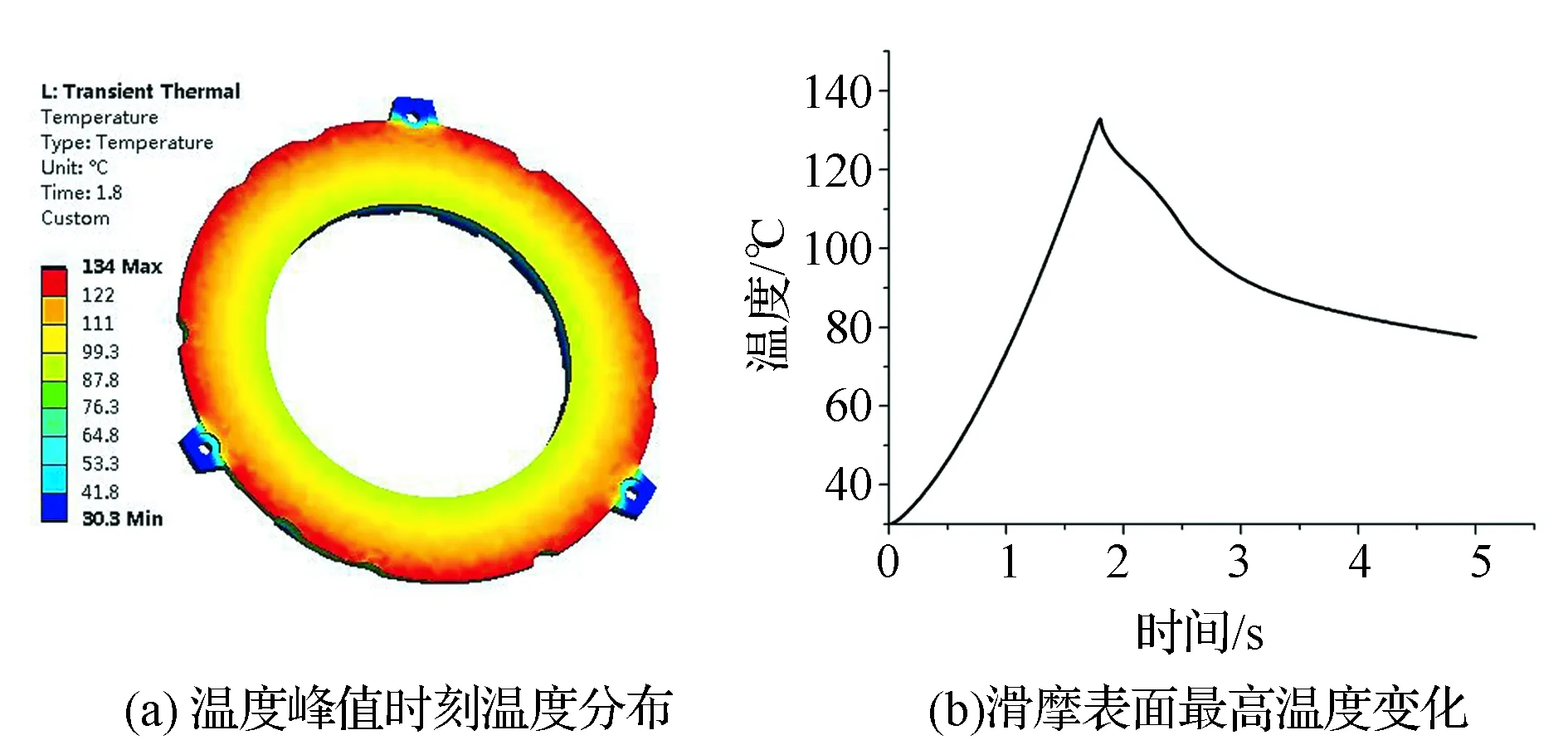
图7 温度场计算结果

由图可见，在汽车满载、坡道起步过程中，离合器一次接合压盘温度达到了134℃，高温区域主要集中在滑摩表面，轴向温度梯度较大。在离合器刚开始接合的过程中，压盘温度快速升高，接合完成之后，温度缓慢下降。

将计算出的温度结果作为载荷施加到压盘上，再对压盘进行热-结构耦合分析。即采用顺序耦合的方法，计算压盘因为受热产生的应力和变形。压盘在接合过程中，膜片弹簧的压力和压盘自身旋转产生的惯性离心力也会产生一定应力；但是，相比于温度载荷产生的应力，这部分应力非常小，因此在进行热结构耦合分析的过程中，忽略膜片弹簧压力和压盘自身旋转的影响。热结构耦合的计算结果如图8和图9所示。压盘缺口摩擦面侧为下缘，支撑面侧为上缘。

图8 压盘缺口下缘应力达到峰值时刻应力分布图

图9 压盘缺口上缘应力达到峰值时刻应力分布图

压盘的整体应力水平较低，但是应力集中现象非常明显。在热应力达到峰值时，压盘应力最大点出现在缺口下缘的中心位置(图8(b))，应力值达到了135.2MPa。在3s时，缺口上缘的应力最大点出现在中心位置(图9(b))，应力值达到了94MPa。压盘的整体应力水平较低，但是应力集中现象非常明显。同时，仿真结果中的应力最大值位置与断裂位置一致，也验证了模型的正确性。

图10为压盘缺口上、下缘最大应力值随接合时间变化的曲线。由图可见：在接合开始后，下缘应力快速增大，在2s时达到峰值，并开始缓慢下降；上缘应力在接合开始时应力并不大，在1.5s时刻之后开始显著增加，在3s时达到峰值，而后缓慢下降。出现这种现象的原因主要是：在接合刚开始时，滑摩产生大量的热量，同时由于时间较短，热量在轴向传递较少，高温区域全部集中在滑摩表面；缺口下缘处轴向温度梯度较大，因此应力水平较高。在接合完成后，滑摩表面温度梯度降低，但是由于热量的轴向传递，缺口上缘处的温度梯度增加，因此，应力水平较高。

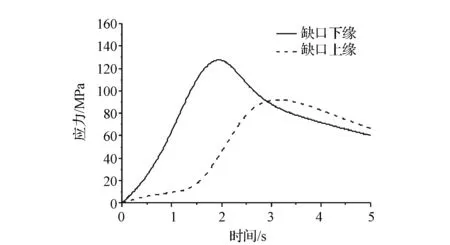
图10 缺口上下缘应力曲线

3 压盘结构改进

综上所述，在汽车起步、离合器接合过程中，压盘应力最大值出现在缺口下缘，而在接合完成时，应力最大值出现在缺口的上缘。因为压盘的材料参数很难改变，并且由于离合器工作环境相对封闭，与周围的换热情况也很难改变；因此本文中主要从压盘缺口半径和压盘厚度两个方面对压盘结构进行改进。改进方案如表2所示。

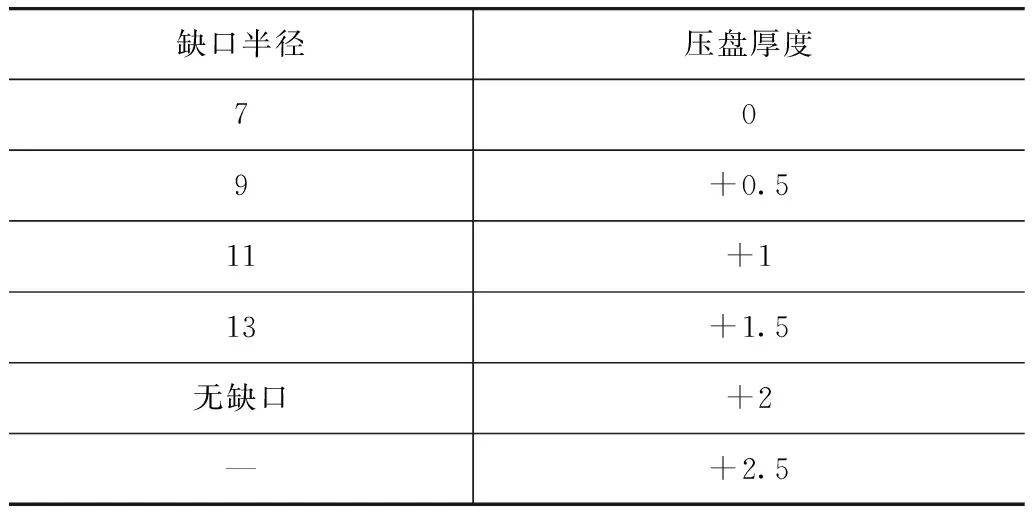
表2 压盘改进方案 mm

3.1 缺口半径对热应力大小的影响

压盘因受热而沿径向膨胀是导致缺口处产生应力集中的主要原因。在保证缺口弦长，即缺口宽度不变的情况下，缺口半径的大小会引起缺口深度的变化。分别建立半径为7(初始设计方案),9,11和13mm及无缺口5个有限元模型，进行热结构耦合分析，计算结果如表3所示。

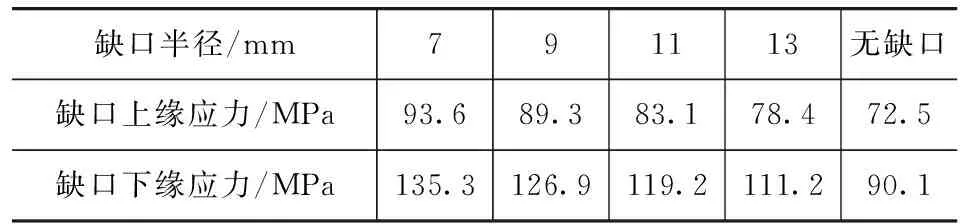
表3 缺口半径对应力的影响

由表可见，由于缺口弦长不变，随着缺口半径的增加，缺口深度减小，应力水平随之降低。从缺口半径为7mm到无缺口；下缘应力值降低了33.4%，上缘应力值降低了22.5%。半径增加，对下缘应力改善效果更加明显，这是因为缺口深度减小可在离合器刚开始接合的阶段有效地降低由于热膨胀而产生的拉应力。

3.2 厚度对热应力大小的影响

压盘厚度增加，可影响热量在轴向传导的效率，且增加缺口的厚度，有效降低其应力水平。在原始模型的基础上给压盘加厚0.5，1.0，1.5，2.0和2.5mm，并分别建立有限元模型进行热结构耦合分析，计算结果如表4所示。

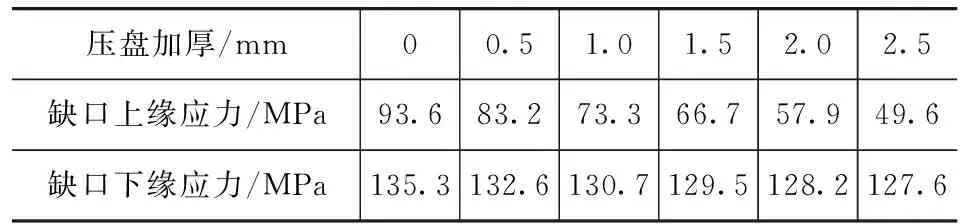
表4 压盘厚度对应力的影响

由表可见，由于压盘加厚，缺口应力水平也在降低。从初始设计方案到压盘加厚2.5mm，下缘应力值降低6.0%，上缘应力降低47%。厚度增加对缺口上缘应力改善效果非常明显，而对下缘应力只稍有改善。这是由于厚度增加并不能改变离合器刚开始接合时由于热膨胀对缺口产生的拉应力。但由于厚度增加，轴向温度梯度降低，所以缺口上缘的应力水平明显降低。

3.3 压盘最终方案

根据以上分析，最终将原压盘断裂处缺口去除(共3处)，压盘厚度增加2.5mm，改进后压盘如图11(b)所示。而原来为之而设置缺口的干涉问题，则通过调整飞轮上的离合器定位铆钉的位置和改变离合器总成的安装半径予以解决。

对改进后的压盘进行有限元热结构耦合计算并与改进前计算结果进行对比，结果如表5所示。由表可见，改进后压盘原缺口处上缘热应力下降62.1%，下缘热应力下降40.6%，均有明显下降。将改进后的离合器压盘制成样品进行装车测试。在测试过程中，改进后的离合器运行良好，未出现压盘断裂情况。

图11 改进前后离合器压盘

表5 压盘改进前后热应力对比 MPa

综上所述，本文中的建模和分析方法能对压盘在使用过程中应力集中位置有较为准确的预测。在压盘的设计开发过程中，原先为避免与离合器壳的连接铆钉产生干涉而在压盘外缘设计了缺口，但分析结果表明设置缺口后，压盘在该处的压力明显增大，故最终取消缺口，干涉问题通过其它措施解决。压盘的总体厚度也由于安装空间的限制有一定的尺寸限制。在压盘设计受到这些条件的约束时，利用本文中的建模和分析方法，能够有效地确定压盘的最优结构，降低在使用时由于温升而产生的应力水平，并改善应力集中的现象，为压盘的设计开发提供了有效依据，缩短了设计开发周期，提高了压盘在使用过程中的可靠性。

4 结论

(1) 本文中在考虑了波形片轴向非线性特性以及摩擦因数随转速差变化的离合器传递转矩模型，并计算得到了离合器接合时产生的滑摩功和滑摩功率。建立了压盘温度场分析的有限元模型，计算得到压盘滑摩表面温度，并通过试验验证了模型的正确性。

(2) 建立了发动机传递转矩模型和离合器动力学模型；并对压盘进行了热结构耦合分析。结果表明：在离合器接合过程中，压盘的整体应力水平较低，但是应力集中现象非常明显，应力最大值出现在压盘的缺口处，与压盘实际断裂位置一致。

(3) 通过增加压盘缺口半径和压盘厚度两个方面对压盘进行结构改进。结果表明：随着缺口半径的增加，缺口深度减小，压盘缺口下缘应力水平明显降低，最终决定取消缺口。随着厚度的增加，轴向温度梯度减小，压盘缺口上缘的应力水平明显降低。将改进的压盘进行装车测试，在整个测试过程中，离合器运行良好，未出现压盘断裂情况，表明本文中的建模和分析方法对离合器压盘的设计与开发具有指导意义。

[1] VASCA F, IANNELLI L, SENATORE A， et al. Modeling torque transmissibility for automotive dry clutch engagement[C]. American Control Conference, 2008： 306-311.

[2] VASCA F, IANNELLI L, SENATORE A, et al. Torque transmissibility assessment for automotive dry-clutch engagement[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(3):564-573.

[3] WANG Y, LI Y, LI Nan, et al. Time-varying friction thermal characteristics research on a dryclutch[J]. Proc. IMechE Part D:J Automobile Engineering，2014，228(5): 510-517.

[4] ABDULLAH O, SCHLATTMANN J. Computation of surface temperatures and energy disspation in dry friction clutcches for varying torque with time[J]. International Journal of Automotive Technology,2014, 15(5): 733-740.

[5] ABDULLAH O, SCHLATTMANN J.Finite element analysis of temperature field in automotive dry friction clutch[J]. Tribology in Industry, 2012, 34(4):206-216.

[6] ABDULLAH O, SCHLATTMANN J.Effect of band contact on the temperature distribution for dry friction clutch[J]. Tribology in Industry, 2013, 35(4):317-329.

[7] VELARDOCCHIA M, AMISANO F, FLORA R. A linear thermal model for anantomotive clutch[C]. SAE Paper 2000-01-0834.

[8] 蔡丹，魏宸官，宋文悦. 离合器片表面温度的测量与表面应力的计算[J]. 车辆动力与技术，2000,4(1):7-11.

[9] HE H, OKUBO K, FUJII T, et al. Thermal deformation of pressure plates for manual clutch[C].SAE Paper 2005-01-1784.

[10] 栾文博，吴光强. 基于六自由度传动系模型的自动变速器仿真[J]. 农业机械学报，2013(4)：1-7.

[11] 刘雪莱，朱茂桃. 离合器压盘热负荷特性分析及改进研究[J]. 机械传动，2014, 38(5):128-131.

[12] 胡建军，李光辉，伍国强，等. 汽车起步过程离合器传递转矩精确计算分析[J]. 汽车工程，2008,30(12):1803-1806.

A Method of and its Application to the Thermal Deformation and Stress Analyses for Clutch Pressure Plate

Wan Lixiang1, Chen Hao1, Liu Xuelai2, Hou Qiufeng3, Yu Yang4& Shangguan Wenbin2

1.SchoolofMechanicalEngineering,SouthwestJiaotongUniversity,Chengdu610031;2.SchoolofMechanicalandAutomotiveEngineering,SouthChinaUniversityofTechnology,Guangzhou510641;3.NingboHongxieClutchCo.,Ltd.,Ningbo315807;4.TianjinFawXialiAutomobileCo.,Ltd. ,Tianjin300380

To solve the fracture problem of clutch pressure plate, a model for analyzing the thermal deformation and stress of pressure plate is built with consideration of the changes in axial nonlinear characteristics of waved plate and friction coefficient with rotating speed difference. With the model, the temperature distribution during the engaging process of pressure plate is simulated and verified by real measurement. Based on analysis results, modification schemes for pressure plate are proposed, a sample part is produced and real vehicle test is performed with no fracture of pressure plate happened, demonstrating the correctness of modeling and analyses.

clutch; pressure plate; temperature field analysis; temperature measurement; thermo-structure coupling

*国家自然科学基金(11472107，51475171)和广东省自然科学基金(2014A030313254)资助。

原稿收到日期为2015年8月5日，修改稿收到日期为2015年11月20日。