盘式制动器闭环耦合模型耦合刚度的优化
高 普,杜永昌,王宇健
(1. 北京理工大学机械与车辆学院,北京 100081; 2. 清华大学,汽车安全与节能国家重点实验室,北京 100084)
2016214
盘式制动器闭环耦合模型耦合刚度的优化
高 普1,杜永昌2,王宇健2
(1. 北京理工大学机械与车辆学院,北京 100081; 2. 清华大学,汽车安全与节能国家重点实验室,北京 100084)
为确定盘式制动器关键耦合界面的耦合刚度,首先进行制动器静态加压加载工况下的模态试验得到其模态参数,然后运用非线性优化方法使模型计算与试验结果间的误差达到最小,从而得到与实际使用工况尽量一致的耦合刚度。最后将优化后的模型和原模型计算结果与台架试验结果进行对比。结果表明,利用本文优化后的耦合刚度计算得到的不稳定模态结果与台架制动噪声试验结果更接近,验证了本文方法的合理性和有效性。
盘式制动器;制动噪声;闭环耦合模型;耦合刚度;优化
前言
车辆制动时动能通过摩擦副间的相对滑动作用转化为热能耗散,如果制动器设计不合理、摩擦材料老化或制动工况改变,制动时就可能引起强烈的振动,并伴随着噪声。制动噪声不仅降低汽车舒适性、造成噪声污染,而且会造成承载零部件的早期磨损,降低寿命。
对制动噪声的诊断和有效抑制是汽车行业一直面临的问题。由于制动器具有复杂的结构动态特性,且制动噪声产生与多变的使用工况和环境因素密切相关,迄今为止对该问题的研究仍没得到一致的结论[1-2]。然而,在过去的二三十年,大量试验和分析的方法被应用到分析诊断和抑制制动噪声问题中,并取得了显著成果,大大降低了汽车产品的制动噪声水平[3-7]。
复特征值分析方法是对制动噪声进行建模分析的行之有效的方法。文献[8]中首先将盘式制动器制动片与制动盘之间的摩擦耦合作为非对角项引入系统刚度矩阵,以其不稳定复特征根表征系统振动的发散。文献[5]、文献[6]和文献[9]~文献[12]中利用有限元和模态综合法建立了盘式制动器闭环耦合模型,并提出了子结构模态组成分析、子结构模态参数灵敏度分析、制动能量馈入分析等方法,可有效地分析结构参数对噪声的影响,寻找抑制噪声的途径,其分析结果与试验有较好的一致性。
在制动器闭环耦合模型中,子结构(零部件)的动态特性以模态参数表示,而子结构之间的相互作用以耦合节点间的弹性和摩擦耦合表示。耦合刚度是模型的重要参数,其取值对建模准确性有决定性影响。但公开发表的文献对此问题论述很少。文献[5]和文献[13]中认为耦合刚度的取值应尽量在力学上与原结构等效,文献[14]中则认为应以耦合部位局部刚度的1 000倍作为接触界面的耦合刚度值,文献[15]中在建立盘式制动器整体有限元噪声分析模型时给出了以下原则:(1)两子结构之间存在相对滑动,接触界面的切向耦合刚度设置很小的值,约为0.5N/m;(2)两子结构之间存在严格的相互约束时,耦合刚度设定为较大值,其数量级为1010N/m;(3)两子结构之间存在连续性接触,且材料参数相近时,耦合刚度值数量级设定为109N/m;(4)两子结构之间存在间隔性接触时,耦合刚度值的数量级设定为106N/m。
可见,上述文献[5]和文献[13]~文献[15]中只是给出了一些原则性的建议,在具体建模时需进行大量的试算和调整,并根据模型计算结果判断取值的合理性。这一过程不仅费力、耗时,而且极大地依赖个人的经验和判断。
本文中为一盘式制动器建立了闭环耦合模型,并在确定子结构耦合刚度方面进行研究。首先根据不同耦合界面耦合刚度对模型影响的大小分为关键和次要耦合界面两类。对于次要耦合界面的耦合刚度,参照文献给出的原则和以往的建模经验确定;对于关键耦合界面的耦合刚度,则进行制动器静态加压加载工况下的模态试验得到其模态参数,然后运用非线性优化算法,使模型计算与试验得到的结果间的误差达到最小,从而得到与实际使用状况尽量一致的耦合刚度。最后对利用优化得到的耦合刚度和现有根据经验确定的耦合刚度参数计算出的不稳定模态,与台架制动噪声试验结果进行对比。结果表明,利用本文中优化得到的耦合刚度计算得到的不稳定模态结果与台架制动噪声试验结果的一致性有显著提高,证明了本文中方法的合理性和有效性,应用于后续的噪声分析,可提高分析结果的可信度,并有助于制定更有效的噪声抑制措施。
1 盘式制动器闭环耦合模型
闭环耦合模型是基于制动器结构闭环耦合理论和模态综合方法建立的分析模型[5,9,12]。
在忽略子结构本身的小阻尼的情况下,制动器的振动方程为
(1)式中:M和K分别为有限元离散化后的质量阵和刚度阵,它们分别由各子结构的质量阵和刚度阵组合而成;u为所有节点的位移矢量;Kf为摩擦耦合刚度阵,是非对称阵,由子结构间的相互作用关系确定。
设q为子结构模态坐标矢量,则
u=Φq
(2)
式中Φ为由各子结构对各自模态质量归一化的模态振型矩阵组合而成的矩阵。
利用式(2)对式(1)进行坐标变换可得
(3)
其中:
Ksys=λ-ΦTKfΦ
(4)
式中λ为各子结构的模态角频率平方组成的对角阵。
对式(3)进行复特征分析,可得到系统的复特征值和相应的特征向量。复特征值虚部表示噪声频率,实部代表模态阻尼。因此实部大于零的模态为负阻尼,对应于系统中不稳定的、存在产生尖叫倾向的模态,称为噪声模态。噪声模态复特征值实部越大,说明发生噪声的倾向越大。
由式(4)可以看出,在子结构模态参数已经确定的情况下,建模质量取决于摩擦耦合矩阵Kf。要得到可信度高的复特征值分析结果,就必须使Kf与噪声发生时的实际状况尽量一致。
2 耦合刚度矩阵
制动器闭环耦合模型以子结构间的耦合表示零部件之间的相互作用。本文中所建模型包含7种耦合界面,如表1所示。
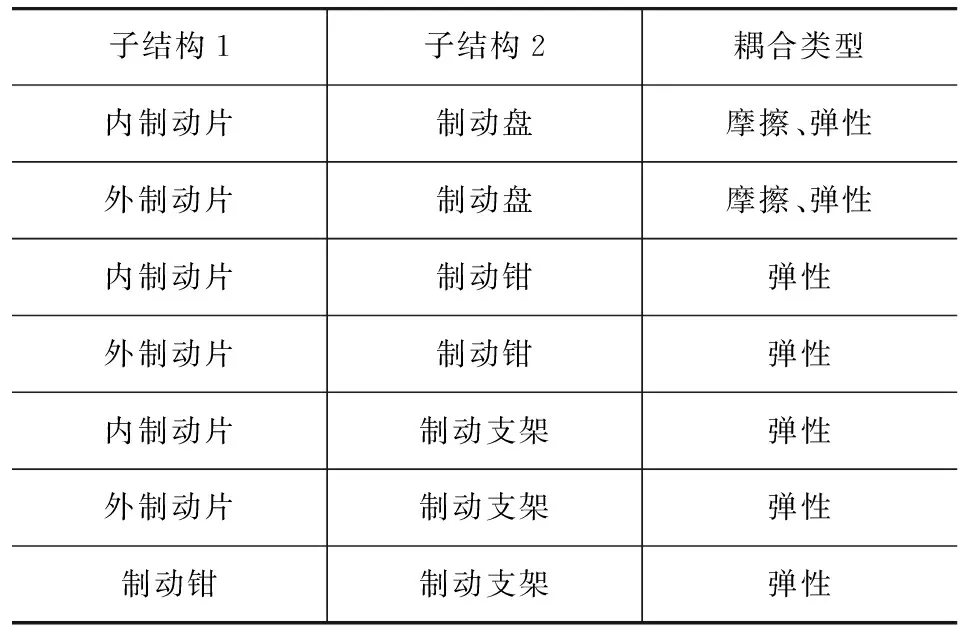
表1 子结构间的耦合类型
耦合刚度矩阵具体描述耦合界面内节点之间的耦合。制动片摩擦材料和制动盘之间的耦合界面同时存在弹性和摩擦耦合,其耦合节点对间的耦合刚度矩阵[5-6]可表述为
(5)
其他的耦合界面只存在弹性耦合,其耦合矩阵[5]简化为
(6)
式(5)和式(6)中:μ和K分别为摩擦因数和节点耦合刚度。
3 次要耦合界面参数
不同的耦合界面参数对模型有不同的影响。根据经验,相比其它耦合界面,制动片摩擦材料与制动盘之间和内制动片背板与制动钳之间的耦合参数对闭环耦合模型的计算结果影响巨大,细微的取值变化会使后续的计算结果发生质变,在本文中称为关键耦合界面,而其它耦合界面被称为次要耦合界面。针对这两种不同的耦合界面,本文中分别采用不同的方法确定其耦合刚度的取值。
对于次要耦合界面的耦合刚度可根据已有经验和文献给出的原则确定取值范围:
(1)某些耦合界面为性质接近的两个平整金属表面连续性接触,如制动钳与外制动片背板接触界面、制动片背板耳槽与支架安装凸台的接触界面等,其取值范围在109N/m附近;
(2)某些耦合界面存在油膜润滑,如制动导向销与支架导向销孔壁接触界面,其耦合刚度值取决于油膜,大体估计接触刚度值为106N/m左右。
4 关键耦合界面参数
关键耦合界面指同时存在弹性和摩擦耦合的制动盘与两个制动片的接触界面和内制动片背板与制动钳的接触界面。本文中首先对制动器进行静态加压加载工况下的模态试验,得到其模态参数,然后运用非线性优化算法,使模型计算结果与试验数据的误差最小,优化得到与实际状况尽量一致的耦合刚度取值。
4.1 制动总成静态加压加载模态试验
静态加压加载模态试验在制动器静止工况下进行。制动器固定在牢固的支架上,在安装轮辋的位置安装加载横杆。试验时,制动管路内施加并保持稳定的制动压力,制动盘静止并使加载横杆保持水平,在加载杆末端吊装一定数量的砝码以模拟制动力矩,这样可使各个零部件之间的耦合受力状态与实际制动时尽量接近。采用力锤对制动盘进行垂直方向激励,在制动盘、制动钳和支架上安装三向加速度传感器,利用LMS数据采集设备采集试验数据,试验装置如图1所示。

图1 制动器静态加压加载试验装置
通过试验提取了6.5kHz内的5阶模态,其模态参数见表2。由于多数模态制动盘在轴向的振型幅值较大,形状规则,因此只给出了制动盘的外廓的轴向振型并在振型图中以放大的径向变形表示。
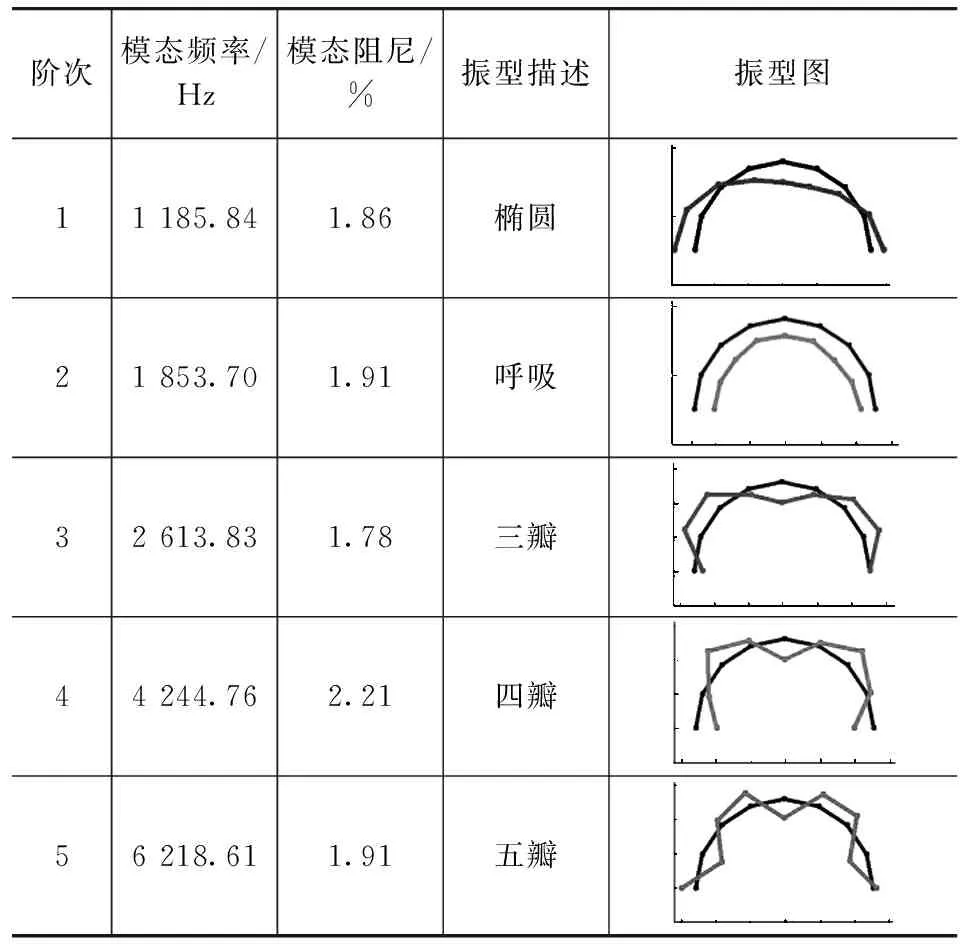
表2 制动器静态加载模态试验结果
本文中挑选后3阶辨识度高的振型的模态,作为后续优化工作的目标。
4.2 制动器模型调整
由于试验是在静态加压加载条件下进行的,因此必须对制动器闭环耦合模型进行调整使之与试验条件相符。模态试验时制动器各部件只存在高频小振幅的振动,可认为耦合界面间无相对滑动,只有静摩擦力,因此式(5)矩阵中的不对称项不再出现,而是以等效刚度耦合的形式存在。经此变换后,系统特征矩阵变为对称阵,式(3)的特征值实部全部为0,即此工况下系统的各阶模态全部为稳定模态。
4.3 优化方法
优化的目的是寻找关键界面耦合刚度的最优解使模型计算得到的模态参数与模态试验结果之间的误差最小,优化的目标函数[16-17]设定为
(7)
其中:
Wjf=(ω1e/ωje)2,j=1,…,N
(8)
式中:ωjl和ωje分别为模型计算和模态试验得到对应的N个模态频率;Wjf为第j阶加权系数。
优化变量为关键耦合界面耦合刚度,包括制动盘与制动片摩擦材料界面耦合刚度和制动钳与内制动片背板界面耦合刚度。在优化前首先需要确定优化变量的初始值和取值范围。
(1)制动盘与制动片界面耦合刚度:根据有限元静力计算和以往研究经验确定其初始值为5×107N/m,取值范围为2×107~1×108N/m。
(2)制动钳与内制动片背板界面耦合刚度,代表制动管路的弹性,与制动液压系统的体积弹性模量成正比,可估算为
(9)
式中:CT为刚度;E为液压系统的体积弹性模量;A为制动缸截面积;V为制动缸和制动管路内的制动液总容积。根据文献[18],E大致范围为500~1 400MPa,因此可估算耦合刚度范围为5×106~5×107N/m,初始值为3×107N/m。
对于优化目标函数和优化变量初始值的取值范围,运用序列二次规划算法(SQP)进行寻优。其基本思想为:在某个近似解处将原来的非线性规划问题简化为一个二次规划问题,求其最优解[19]。对于约束优化问题,可把非线性目标函数与其约束条件相结合,构造拉格朗日函数,进行二次近似求解,将求得最优解代替原函数的解。在优化过程中涉及的拉格朗日函数的海赛矩阵,可利用拟牛顿法的近似计算,这里采用BFGS变尺度方法构造其近似值,其中优化步长则利用一维线性搜索获取。
4.4 优化结果
优化过程中,目标函数值随迭代次数增加的变化曲线如图2所示。
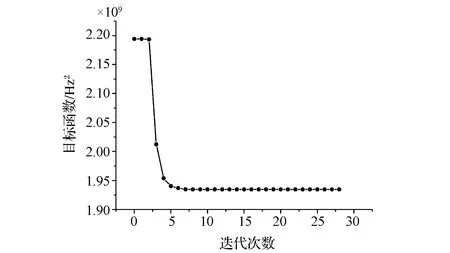
图2 目标函数值随迭代次数变化趋势
由图可见,随着迭代次数的增加,目标函数收敛于一稳定值,说明优化问题达到了最优解。表3为优化前后模型计算得到的模态频率与对应的试验结果之间的对比。
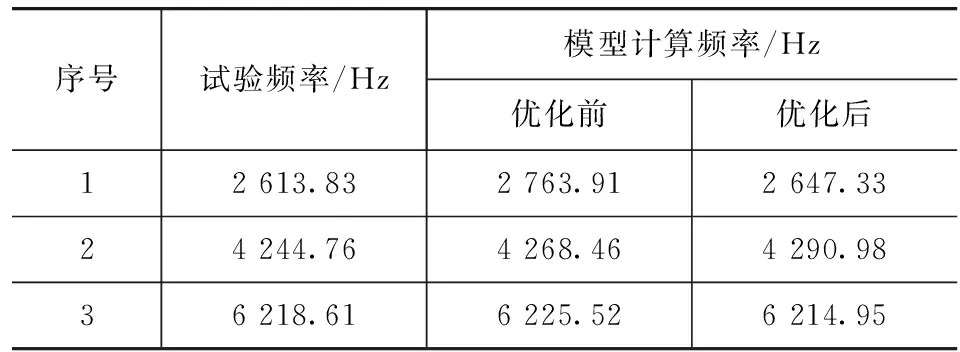
表3 优化前后计算模态频率与试验结果对比
从表3可以看出,经过耦合刚度优化后模型计算结果更加接近试验得到的模态频率。可以推断,这时的关键耦合界面的耦合刚度取值更加接近制动器的实际情况。
耦合刚度最优值:制动盘与制动片耦合界面为4.9×107N/m;制动钳与内制动片耦合界面为2.6×107N/m。
表4列出了最终确定的两类耦合界面的耦合刚度取值。

表4 耦合刚度最终取值
5 复特征分析结果
本文中最后将优化得到的耦合刚度参数代入制动器闭环耦合模型,进行复特征值分析,得到其不稳定模态,与根据文献[5]中经验选定的耦合刚度计算出的不稳定模态和目标制动器台架试验得到的制动噪声结果进行对比,如图3所示,图3(a)为台架噪声试验结果,图3(b)为优化前后模型仿真计算出不稳定模态的两组结果。
首先观察图3中的台架噪声试验结果,根据不同频率处发生高声压噪声的频次判断制动器的噪声产生倾向,可以看出,在1.6,2.7,4.3,5.5,7.5,8.5,8.7,10和13kHz处测得多次的制动噪声,其中1.6,2.7,8.5和13kHz附近出现频次最高。然后对比优化前后两模型计算出的不稳定模态,前者计算出了2.7,7.5,10和13kHz附近的不稳定模态,且10和13kHz这两阶不稳定模态的复特征根实部最大;而后者比前者多计算出了1.6,4.3,8.5和8.7kHz附近的不稳定模态,且1.6,8.5和13kHz这3阶不稳定模态的复特征根实部最高。因此可以看出,利用优化得到的耦合刚度建立的模型所得到的不稳定模态无论在频率的分布上,还是复特征根实部所指示的不稳定倾向上,都比原模型与台架试验结果一致性更好,说明此模型更加接近目标制动器的实际情况。

图3 台架试验及模型计算结果
6 结论
本文中利用结构闭环耦合理论建立盘式制动器分析模型,并通过制动器静态加压加载工况模态试验和参数优化得到了更接近制动器实际情况的耦合参数。与台架制动噪声试验结果对比表明,利用本文中优化得到的参数建立的制动器模型与试验数据的一致性有显著提高,证明了本文中方法的合理性和有效性,应用于后续的噪声分析,可提高分析结果的可信度,并有助于制定更有效的噪声抑制措施。
[1] CHEN F.Disc brake squeal:an overview[C].SAE Paper 2007-01-0587.
[2] OUYANG H, NACK W, YUAN Y, et al. On automotive disc brake squeal part II: Simulation and analysis[C]. SAE Paper 2003-01-0684.
[3] LIU W, PFEIFER J. Reducing high frequency discbrake squeal by pad shape optimization[C]. SAE Paper 2000-01-0447.
[4] YUE Y, ALLGAIER R, JABER N, et al. Brake noise study (part I): low frequency squeal[C]. SAE Paper 2006-01-0474.
[5] 蒋东鹰. 盘式制动器制动尖叫的研究[D].北京:清华大学汽车工程系,1998.
[6] 宿新东. 抑制制动器振动噪声的子结构灵敏度分析和结构修改设计方法研究[D].北京:清华大学汽车工程系,2003.
[7] 张芳, 管迪华. 抑制制动器振动噪声的阻尼方法的探讨[J]. 汽车工程, 2003, 25(3): 264-268.
[8] LILES G. Analysis of disc brake squeal using finite element methods[C]. SAE Paper 891150.
[9] GUAN Dihua, JIANG Dongying. A study on disc brake squeal using finite element methods[C]. SAE Paper 980597.
[10] GUAN Dihua, SU Xindong, ZHANG Fang. Sensitivity analysis of brake squeal tendency to substructures’ modal parameters[J]. Journal of Sound and Vibration, 2006, 291(1): 72-80.
[11] GUAN Dihua, HUANG Jinchun. The method of feed-in energy on disc brake squeal[J]. Journal of Sound and Vibration, 2003, 261 (2): 297-307.
[12] 管迪华,杜永昌,王霄锋,等. 对一盘式制动器高频尖叫及抑制的分析[J]. 工程力学, 2014(12):217-222.
[13] 孙振华, 蒋东鹰. 盘式制动器制动尖叫的研究[J]. 汽车工程, 1999, 21(6): 326-332.
[14] CHEN F, TAN C, QUAGLIA R L. Disc brake squeal: mechanism, analysis, evaluation, and reduction/prevention[M]. SAE International, 2006: 83-84.
[15] ABU-BAKAR A R, OUYANG H. Recent studies of car disc brake squeal[J]. New Research on Acoustics:159-198.
[16] 李效韩,杨炳渊. 结构振动分析中的连接子结构[J]. 宇航学报,1987(1):7-15.
[17] 宋伟力,杨炳渊. 舵-液压伺服机构刚度参数识别[J]. 强度与环境,1992(4):1-5.
[18] 戴云飞. 液压缸液压刚度的计算[J]. 有色金属设计, 1999(1).
[19] GAO P, DU Y, WANG Y. Validation of closed-loop coupling disc brake model for squeal analysis[M]. Experimental Techniques, Rotating Machinery, and Acoustics, Volume 8. Springer International Publishing, 2015: 113-120.
Optimization of Coupling Stiffness Obtained from Closed-loop Coupling Model for a Disk Brake
Gao Pu1, Du Yongchang2& Wang Yujian2
1.SchoolofMechanicalandVehicularEngineering,BeijingInstituteofTechnology,Beijing100081;2.TsinghuaUniversity,StateKeyLaboratoryofAutomotiveSafetyandEnergy,Beijing100084
For determining the coupling stiffness of key coupling interfaces in a disk brake, firstly a modal test is performed on a stationary disc brake with both hydraulic pressure and braking torque applied to get modal parameters. Then non-linear optimization method is used to minimize the differences between the results of model calculation and stationery modal test, thus a coupling stiffness is obtained which is as close as possible to the real operation condition. Finally the results with optimized model and original model are compared with bench test results. The outcomes show that the unstable modes calculated with the coupling stiffness obtained from optimized model are closer to the results of brake squeal bench test than that with original model, verifying the rationality and effectiveness of the method proposed.
disc brake; braking squeal; closed-loop coupling model; coupling stiffness; optimization
*原稿收到日期为2015年7月31日,修改稿收到日期为2015年12月9日。

