从一题多解中探寻一般规律
——由2019年全国卷Ⅱ文科第12题引发的思考
2019-11-19 04:00甘肃
教学考试(高考数学) 2019年6期
甘肃
焦永垚
(作者单位:甘肃省兰州市第六中学)
2019年全国卷Ⅰ和全国卷Ⅱ中的小题压轴题都考到了双曲线的知识,全国卷Ⅰ理科第16题和全国卷Ⅱ文科第12题从表面上看似乎没有联系,但是经过深入挖掘会从全国卷Ⅱ文科第12题的一些解法中发现一般性的结论,并且用此结论可以解决全国卷Ⅰ理科第16题.本文将通过对这两道题的多解探寻总结出解决高考圆锥曲线小题的一般方法,让学生轻松突破解决这类问题的思维瓶颈.
一、题目
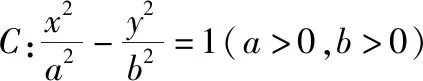
( )
2018年1月,《普通高中数学课程标准(2017年版)》正式发布,其中提出数学六大核心素养,并界定了数学核心素养的含义,本题就是逻辑推理、直观想象、数学运算等数学核心素养的具体体现.
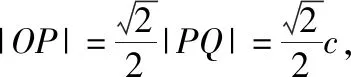
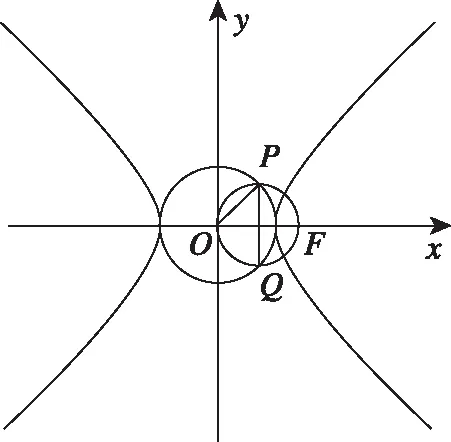
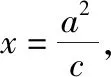
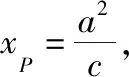
从上述解法可以看出,解法1是通法,而由解法2和解法3可以得出以下重要的结论.
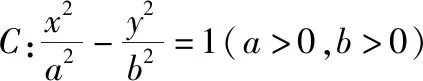
(1)直线PQ为双曲线的准线;
(2)点P,Q在双曲线的渐近线上.
再来看2019年全国卷Ⅰ理科第16题,虽然表面上看与2019年全国卷Ⅱ文科第12题没有关系,但是经过挖掘可以发现,这两道题有着本质的联系,并且该题可以应用上述结论来解决.
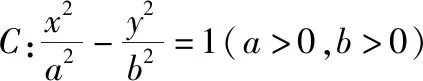
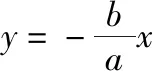
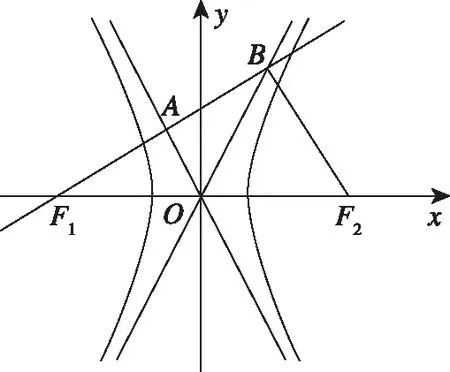
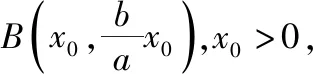
【点评】有意思的是从解法2中可以发现,点B恰好是直线x=±a,y=±b所围成的矩形的顶点.另外,直接运用向量的坐标运算也是解决本题的通性通法.
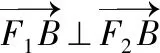
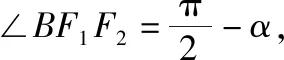
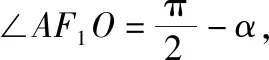
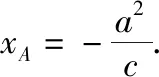
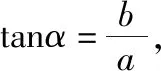
教师应该把教学的重心放到探索问题的过程上,放在揭示问题蕴含的规律上,让学生通过对问题的感知、概括、应用,去发现和掌握规律.上述两道高考题及所蕴含的规律就是这一过程的具体体现.通过进一步挖掘我们还可以找到上述问题的源头.
二、追本溯源
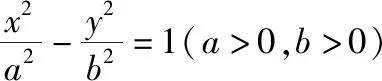
( )
A.30° B.45°
C.60° D.90°
答案:D
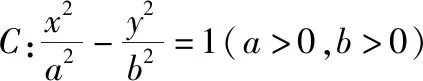
( )
A.2 B.3
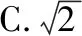
答案:C

猜你喜欢
意林(2021年21期)2021-11-26
中学生博览·文艺憩(2020年3期)2020-08-14
中学生数理化(高中版.高二数学)(2018年2期)2018-04-04
中学教学参考·理科版(2017年8期)2018-02-24
中学生数理化·教与学(2017年1期)2017-01-19
福建中学数学(2016年7期)2016-12-03
数学学习与研究(2016年19期)2016-11-22
创业家(2015年4期)2015-02-27

