无刷双馈电机多回路绕线转子性能研究

周 韬，薛令军，穆 彤

(天津市特种设备监督检验技术研究院，天津 300192)

0 引 言

无刷双馈电机(Brushless Doubly-Fed Machine，BDFM)通过容量较小的变频器控制就可以实现能量的双向流动，可作为发电机或电动机运行，因省掉了电刷和滑环可靠性大大提高[1]。

BDFM的转子结构直接影响着电机性能，近年来对绕线式BDFM转子的研究越来越多。绕线式转子槽内的导体可以灵活放置，与功率绕组和控制绕组极对数pp和pc所对应的绕组系数较高，高次谐波含量低。文献[2]根据交流电机绕组理论提出了采用变极法设计绕线转子的理论，利用该方法可以提高槽内导体的利用率，但是接线比较复杂。文献[3]和文献[4]主要对同心式转子绕组设计方法进行了分析，而且每巢只有一个闭合回路，绕组端部较长。文献[5]和文献[6]研究了BDFM气隙中的磁场等内容。文献[7]和文献[8]反应了近些年对BDFM转子结构的研究方向，主要针对不同结构的转子的理论研究。以上文献基本反映了BDFM绕线转子的研究现状。然而，转子结构对改善BDFM的性能、提高其功率密度还需要进行深入的探讨。

BDFM中定子产生的两种旋转磁场通过转子绕组的调制作用产生耦合，实现能量的传递。电机的转子起着极数转换器的作用，不同的转子结构具有不同的磁场调制效果。本文依据交流电机绕组理论，依照齿谐波法设计了一种的每相多个自闭合回路的绕线式转子，给出了多回路绕线转子BDFM统一坐标系下的数学模型，并分析了定转子的谐波磁动势。最后，给出了一个每相3个回路的电机模型算例，并对其进行了有限元仿真研究。

1 结构与数学模型

1.1 转子绕组齿谐波原理

交流电机绕组通常嵌放在铁心表面的槽内，当按p对极设计的分布绕组通电时会产生各种极对数的一系列的磁动势，而磁动势的幅值与其极对数成反比，与其绕组系数成正比。当磁动势的谐波次数与绕组设计极对数p和电机槽数z呈现出如下关系：

vnz±p=nz±p(n=1，2，3…)

(1)

这些磁动势的绕组系数的绝对值与磁动势的绕组系数相同，即

(2)

通常极对数满足式(1)的谐波称为“齿谐波”。

式中，含“+”的齿谐波磁动势旋转方向与基波相同，含“-”的与基波相反。这也说明齿谐波磁动势是成对出现的。

根据BDFM的工作原理，转子必须同时产生与功率绕组和控制绕组的极对数pp和pc所对应的两种旋转磁动势，且这两种磁场的旋转方向相反。这恰好可以利用齿谐波理论，把其中极对数为pp的磁动势波当成基波，把它的一阶反向的齿谐波看成另一种极对数pc的磁动势波即可；另一方面，由于两种极对数绕组系数相同，只要将pp设计成较高的绕组系数，另一极对数pc绕组系数也自动会较高。

齿谐波法设计的BDFM的两种极对数pp和pc，与转子槽数Zr应满足的关系为

Zr=n(pp+pc)(n=1，2，3…)

(3)

式(3)表明，为了获得两种极对数的磁动势，在对称性的前提下，转子槽数为两种极对数之和的整倍数即可。实际上为了有效的加强这两种极对数的磁动势，削弱其他高次谐波，通常将转子槽数设计为两种极对数之和的偶数倍，即进行“裂槽”使得两种极对数的绕组系数都较高。

1.2 多回路转子结构

BDFM的定子上放有两套三相绕组，也就是极对数为pp的功率绕组和极对数为pc的控制绕组，且它们相互独立。功率绕组接入工频电网，控制绕组接双向变频器。定子两种极对数的三相绕组产生两种极对数的旋转磁场，通过转子绕组耦合实现电机能量的转换。本文主要讨论转子绕组，定子两套绕组均采用双层短距分布绕组结构。根据齿谐波理论，绕线转子可以设计成同心式绕组和等匝短距绕组两种大的类型。本文讨论的转子为等匝短距每相多自闭合回路的绕组结构。

图1 绕线型转子嵌套的单元结构

图1为绕线式BDFM转子绕组的单元结构图。转子槽数为zr，如图所示转子由m个相同结构的相组成(即转子巢个数为m)，每相由n个单独的自闭合回路线圈绕组组成，从左到右编号为1，2，…，n；相邻的相绕组之间有叠压。

图2为转子每相的闭合回路线圈的结构示意图。如图所示，每相的每个闭合回路线圈的上元件边跨越y0个槽，所有线圈的节距均为θy，矩形虚线方框内表示的是转子每相中的某一个自闭和回路，相当于图1中的一个闭合线圈。⊙表示线圈上元件边在一个槽中的导体，⊗表示线圈下元件边在一个槽中的导体。由图可知，每相绕组的上元件共占用ny0个槽，每相相邻两个闭合回路轴线间距离为y0个槽距，相邻的两相轴线之间的距离为zr/m个槽距。

图2 每相(巢)的多个回路示意图

1.3 统一坐标系数学模型

分析BDFM数学模型时，假设电机气隙均匀、忽略电机齿槽效应和端部漏磁、电机内磁场饱和等因素。规定电机线圈的绕组电压、电流和磁链方向按照电动机惯例。电机的电压方程表示为

(4)

式中，usp、usc和ur分别表示定子功率绕组、定子控制绕组和转子绕组的电压矩阵，Rsp、Rsc和Rr分别为定子功率绕组、定子控制绕组的每相的电阻和转子绕组每个闭合回路的电阻，Ψsp、Ψcp和Ψr、分别为定子功率绕组、控制绕组和转子绕组的磁链矩阵。

BDFM各绕组的磁链方程为

(5)

式中，Lsp、isp分别为定子功率绕组的电感、电流矩阵；Lsc、icp分别为定子控制绕组的电感、电流矩阵；Lr、ir分别为转子绕组的电感、电流矩阵；Mspr表示定子功率绕组与转子绕组的互感矩阵；Mscr表示定子控制绕组与转子绕组间的互感矩阵；T表示矩阵的转置。

由于电机转子是旋转的，定子功率绕组、控制绕组和转子绕组的互感矩阵与电机的位置有关；定子功率绕组与转子绕组的互感矩阵Mspr可以表示为

(6)

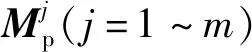
(7)

式中，j=1，2，…m。Mp0为定子功率绕组A相轴线与转子j相绕组轴线重合时的互感值，m为转子的相数(即转子巢数)，θpr为转子第1相绕组轴线超前于定子功率绕组A相轴线的机械角度。

同样，设定子控制绕组A相轴线超前功率绕组A相轴线的机械角度为θ0，则控制绕组与转子绕组的互感矩阵Mcr也是类似的一个3×m阶的矩阵。只是将上式中的θpr换成θpr+θ0，pp换成pc。

转子绕组的自感矩阵Lr表示为

(8)

式中，Lr为一个m×m阶的实对称矩阵，Lj为转子j(j=1，2，…m)相绕组的自感矩阵。由于转子中各相绕组位置相对固定，每相分布的自闭合回路位置相同，故所有相的自感矩阵是相同的。其子矩阵Lj表示为

(9)

(10)

2 磁动势与互感的计算

2.1 绕组磁动势

绕线式BDFM定子两套绕组没有耦合关系，定子绕组磁动势与普通的感应电机无异。由BDFM运行原理可知，定子两套绕组产生的磁场与转子绕组闭合线圈交链，在转子绕组中产生感应电动势，通过闭合的绕组形成感应电流。感应电流的大小和相位主要由转子绕组各相之间的互感和自感以及定转子绕组的互感决定，随转子位置而变化。以单个线圈为基本的分析单元，线圈按空间位置顺序编号，且线圈号与槽号对应。图3表示转子中j相第i个闭合回路中第k个单个线圈的位置示意图，

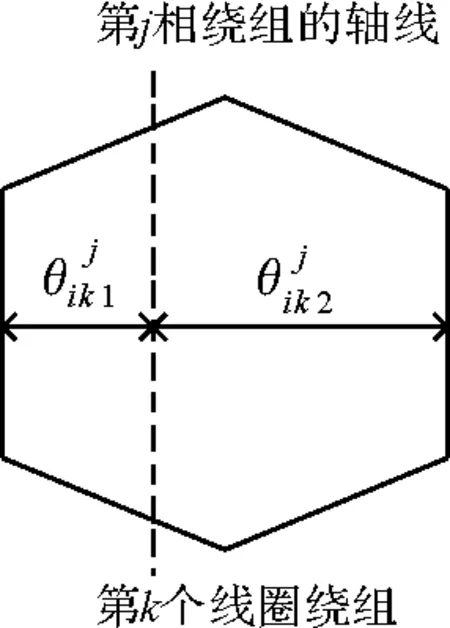
图3 单个线圈位置示意图

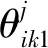
(11)

式中，Bp(vp)为功率绕组产生的极对数为vp的谐波磁密，kryp为转子绕组对极对数为vp的谐波短距系数，l为电机铁心长，D为转子外径，ωp为功率绕组中电流的角速度，ωr为电机转子的机械角速度。由此谐波磁场产生的感应电动势为

(12)

式中，k=1，2，…y0，同理由定子控制绕组电流产生的旋转磁场也会感应出类似的电压，忽略气隙磁动势中的高次谐波，只考虑定子绕组中产生的极对数为pp和pc两种基波旋转磁势产生的感应电压，根据BDFM运行原理，两种基波极对数旋转磁势与转速和极对数关系为

(13)

所以，这两种基波极对数旋转磁势产生的感应电压频率相同。则转子绕组中j相的第i个闭合回路的总电压为

(14)

这样即可得出转子的电压矩阵ur，根据式(4)和式(5)就可以计算出转子的电流矩阵ir。其中j相电流子矩阵ij可具体表示为

ij=[ij1ij2ijn]T

(15)

式中，iji为转子的第j相绕组中第i个回路中的电流值(i=1～n)。由对称性，转子每相中闭合回路绕组感应出的电流产生感应磁动势的轴线与该相绕组的轴线重合。为方便理论计算，假设转子每相中每个闭合回路绕组产生的感应电流幅值相同，均为I0；忽略电流高次时间谐波，则转子j相的第i个闭合回路的电流可以表示为

iji=I0sin(ω0t+φji)

(16)

式中，ω0为电机转子感应电流角速度。φji为j相第i个回路电流的相位。若把坐标原点x=0取在转子第1相绕组的轴线上，则电流iji所形成的旋转的磁势波为

(17)

式中，Fji=ijiNrks/π，ks为槽口系数，cji和cji分别为相应的系数。这样即可表示出转子各相线圈的总的磁势波fr

(18)

2.2 互感的计算

在忽略绕组端部和槽口影响、假设气隙均匀的情况下，根据交流电机绕组理论，1个短路线圈套在转子齿上，匝数为Nr，转子绕组中单个线圈中的电流为i0，则单个线圈产生的总磁势为Nri0。假设磁路线性并忽略定、转子磁路压降。由磁通连续性定理可以得出转子中一个短路线圈在气隙产生的磁动势沿圆周分布图，即图4所示。

在转子绕组中，取机械角度x为横坐标，线圈的节距为θy。则转子j相的第i个回路电流iji共y0个线圈产生的总的磁动势为

(19)

(20)

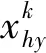
转子绕组任意一个巢中的一个闭合回路的总磁动势就可以表示为

(21)

定子功率绕组与转子绕组的互感最大值，即为式(7)中的Mp0可以表示为

(22)

图4 单个短路回路产生的磁动势示意图

3 算例

3.1 BDFM模型

本文以定子72槽，转子60槽，定子功率绕组8极，控制绕组4极，铁心长为1m的BDFM为例，利用仿真软件建立了二维有限元模型。电机的结构参数如表1所示。

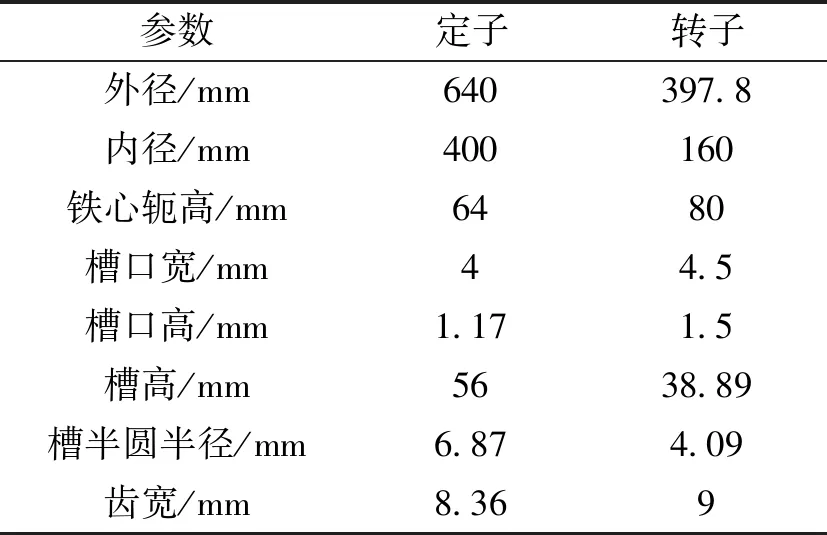
表1 绕线转子无刷双馈电机的结构参数

3.2 转子绕组结构

根据以上分析，综合分析线圈的匝数和节距等手段，设计了一种绕线式的转子结构，图5为每巢3个闭合回路的等匝短距转子绕组接线结构图。

图5 3个自闭和回路等匝短距结构转子接线方式

图中，转子绕组采用每巢3个自闭合回路，每个回路2联等匝绕制，如接线图所示，选择线圈的跨距为8个槽距。显然，转子绕组的第1巢的1号线圈的上层边与6号线圈的下层边分别位于1号和14号槽内，第1巢的第一个自闭合回路分布在第1和第2号槽内，这样的绕法使得转子绕组并没有局限在10个槽距内排布，但每个巢线圈绕组的磁动势矢量分布在宽度为6的槽距内，线圈具有较高的分布系数。而且3个闭合回路的感应电流存在相位差，使每巢的3个回路合成的磁动势的某些高次谐波含量可能会被削弱。

4 有限元仿真

为验证上述分析结果，在其他条件均相同的情况下建立转子每巢3回路绕组和每巢1个回路绕组结构的有限元分析模型，1个回路转子绕组的接线方式如图6所示。电机在超同步状态空载情况下进行仿真，转速均为600r/min，定子功率绕组接380V的工频电网，控制绕组接频率为10Hz、有效值为110V的交流电压源。两种转子结构模型在0.04s时刻的气隙磁密和各谐波含量如图7和图8所示。

图6 1个自闭和回路等匝短距结构转子接线方式

图7 气隙磁密图

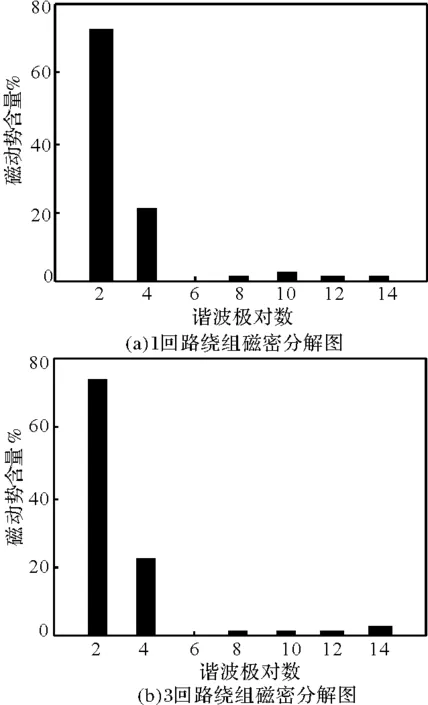
图8 两种对应的转子结构的气息磁密分解图

表2为计算出的两种转子巢结构各次谐波含量与增幅比较。图9为转子第一个巢3个绕组的感应电流波形图。

表2 谐波磁动势所占百分比

图9 转子第一个巢3个回路的电流波形图

通过对比可以看出转子绕组每巢3个自闭合回路时比每巢1个回路的2对极和4对极这两种主极对数气息磁密得到加强，8对极和10对极谐波明显降低，其他高次谐波也有不同程度的减小。由图9可以看出，每巢3回路绕组模型转子中的感应电流相位不同，幅值有差别，由于时间和空间谐波的相互作用呈现出非正弦的形状。

5 结 论

在分析齿谐波法设计等匝短距绕组的基础上，提出了每巢转子绕组多个自闭合回路的绕线转子结构；给出了其数学模型。建立了每巢3个回路的绕线转子算例，利用有限元分析软件对其进行仿真研究，得出了它的气隙磁密波形。通过与每巢1个回路模型仿真结果的分析和对比，得出：当转子每巢有多个自闭合回路时，这些回路中所感应出来的电流波形相差一个相角，幅值也有微小的差异，正是由于这些不同削弱了气隙磁场中的某些高次谐波，从而使两种主要极对数的谐波比例有所提高。因此，这种转子结构有利于改善无刷双馈电机的运行效率，改善其性能。