一种面向电动车IPMSM的基于模糊PI的高性能调速控制方法

谭 琳，刘 平，崔 帅

(1. 广安职业技术学院 智能制造与能源工程学院，四川 广安 638000； 2. 西南交通大学 机械工程学院，四川 成都 610000)

0 引 言

内嵌式永磁同步电机(interior permanent magnet synchronous motor, IPMSM)具有体积小、重量轻以及高功率密度、高转矩输出能力、高可靠性和低噪声、低振动等优点[1]，是电动汽车普遍采用的驱动电机。

矢量控制方法是IPMSM中较为成熟和主流的控制方法，其本质上是通过合理分配定子交轴和直轴电流，实现对电机转矩的控制。由IPMSM运行特点，可将IPMSM运行分为恒转矩区和恒功率区。为充分挖掘IPMSM的扭矩潜力和调速范围潜力，近些年较为普遍的方法是在恒转矩区使用单位电流最大转矩(MTPA)控制算法，在恒功率区则采用弱磁控制算法。控制结构上通常采用内外环结构，内环为电流环，外环为速度环。两环均采用PI控制器进行调节。

PI控制器结构简单，工作可靠，调整方便，在控制对象特性固定时能取得满意的控制效果，工业应用十分广泛。但传统的固定PI控制器缺乏对控制对象特性变化适应能力，而IPMSM作为一个非线性、参数时变、强耦合、干扰繁多的复杂系统，建立准确的数学模型较为困难。同时IPMSM运行于电动汽车上时，负载时变，调速频繁，运行工况较为复杂。传统PI控制器应用在全速度范围IPMSM中会存在超调振荡、稳态误差较大等问题。为改善电机调速动、稳态性能，目前普遍是对各种电机参数、各种电机扰动进行在线辨识，然后进行校正和补偿。刘长柱等[2]采用递推最小二乘法对IPMSM定子电阻、直轴电感、交轴电感、磁链等参数进行在线辨识；林国汉等[3]采用一种改进型综合学习粒子群优化算法在线辨识IPMSM的定子电阻、直轴电感、交轴电感、磁链等参数；肖曦等[4]提出了一种基于遗传算法的参数辨识法来在线辨识IPMSM的定子电阻、直轴电感、交轴电感、磁链等参数；黄文卿等[5]对交流逆变器死区进行了补偿策略，减小了电流谐波对控制系统的影响。以上方法均增加了系统的复杂程度，性能受制于辨识算法性能和收敛时间，且IPMSM干扰繁多，时变参数多，要一一辨识且校正，实际工程实现十分困难。

模糊-PI控制器是一种利用模糊控制器进行实时调整PI参数的自整定方法。它既具备模糊控制器不依赖于控制对象准确数学模型优点，也充分利用了PI控制器良好的控制性能。针对IPMSM特点，笔者设计了一种参数自整定的模糊PI控制方法。通过MATLAB/Simulink环境下仿真，其结果表明：相对于转速环采用固定PI，模糊-PI控制器改善了IPMSM伺服调速系统全速度范围的动、稳态性能，对负载变化等外部干扰及电机参数变化具有较强的鲁棒性，从而更适应电动汽车运行特性。

1 IPMSM数学模型及矢量控制

当忽略磁路饱和、磁滞和涡流等影响，假设定子绕组电流和磁通势均为正弦波分布、无高次谐波时，根据矢量控制理论中的矢量坐标系转换关系，对三相静止(abc)坐标系下的IPMSM数学模型进行Clarke和Park变换可得到两相旋转坐标系(d-q坐标系)下的IPMSM数学模型，分为4组方程：电压方程、磁链方程、转矩方程与运动方程[6-7]，如式(1)～(4)。

磁链方程：

(1)

电压方程：

(2)

电磁转矩方程：

(3)

运动方程：

(4)

式中：λd、λq分别为定子d、q轴的等效磁链；μd、μq分别为定子d、q轴的等效电压；id、iq分别为定子d、q轴等效电流；Ld、Lq分别为定子d、q轴等效电感；TL为负载转矩；Te为电磁转矩即输出转矩；ωr为转子的同步旋转电角速度；R为定子绕组电阻；λPM为永磁体磁链；p为转子极对数；J为转动惯量。

根据IPMSM数学模型，所建立的IPMSM矢量控制系统框图如图1[8]。

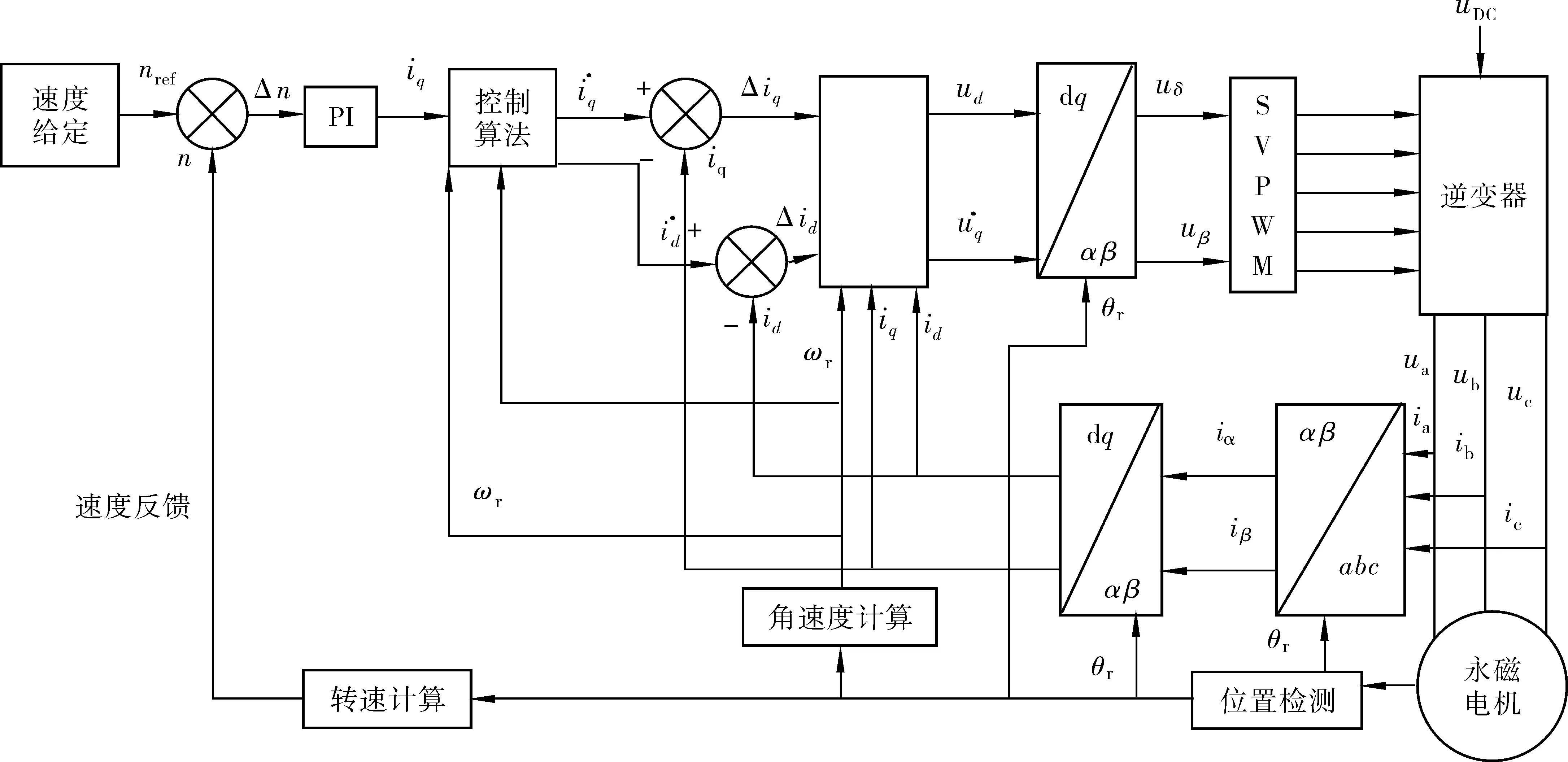
图1 IPMSM矢量控制系统框图Fig. 1 IPMSM vector control system diagram

其中：矢量控制算法在恒转矩区采用最大转矩电流比(MTPA)控制算法，在恒功率区采用弱磁控制算法，从而保证充分挖掘IPMSM的扭矩潜力和调速范围潜力。

2 模糊-PI控制器理论及建模

图1中转速环如采用传统PI控制，其参数整定完全取决于被控对象的数学模型；而模糊控制系统则不同，它并不依赖于被控对象的数学模型，而是通过对人工多次积累操作经验及大量试验数据进行分析、归纳总结，得到适合系统输入输出的模糊关系，特别适用于非线性、时变、滞后系统的控制。考虑到IPMSM特性及在电动汽车上的工况特点，笔者设计了一个模糊-PI控制器，将其取代传统的固定PI控制器，应用于IPMSM伺服调速系统的转速环控制器中。

模糊控制器设计过程主要包括：确定模糊控制器结构、设置输入输出变量及隶属度、建立模糊规则、选定近似推理算法等[9]。模糊控制器控制过程为：把输入量精确值进行模糊化，变成模糊语言表示的模糊输入量，根据模糊控制规则进行模糊决策，得到模糊语言表示的模糊控制量，再进行解模糊处理，得到精确控制量。

笔者所建的模糊-PI控制器(Fuzzy-PI)采用二维输入输出模糊控制器，共有49条模糊控制规则。它能够严格反映受控过程中输出量的动态特性，在控制效果上比一维模糊控制器好[10-11]。Fuzzy-PI以转速偏差e和偏差变化率ec作为输入量，根据模糊规则自动得到PI控制器中比例系统和积分系数的修正值，对这两个系数进行在线调整，使其能适应各种复杂工况、参数变化和扰动。Fuzzy-PI控制器原理如图2。

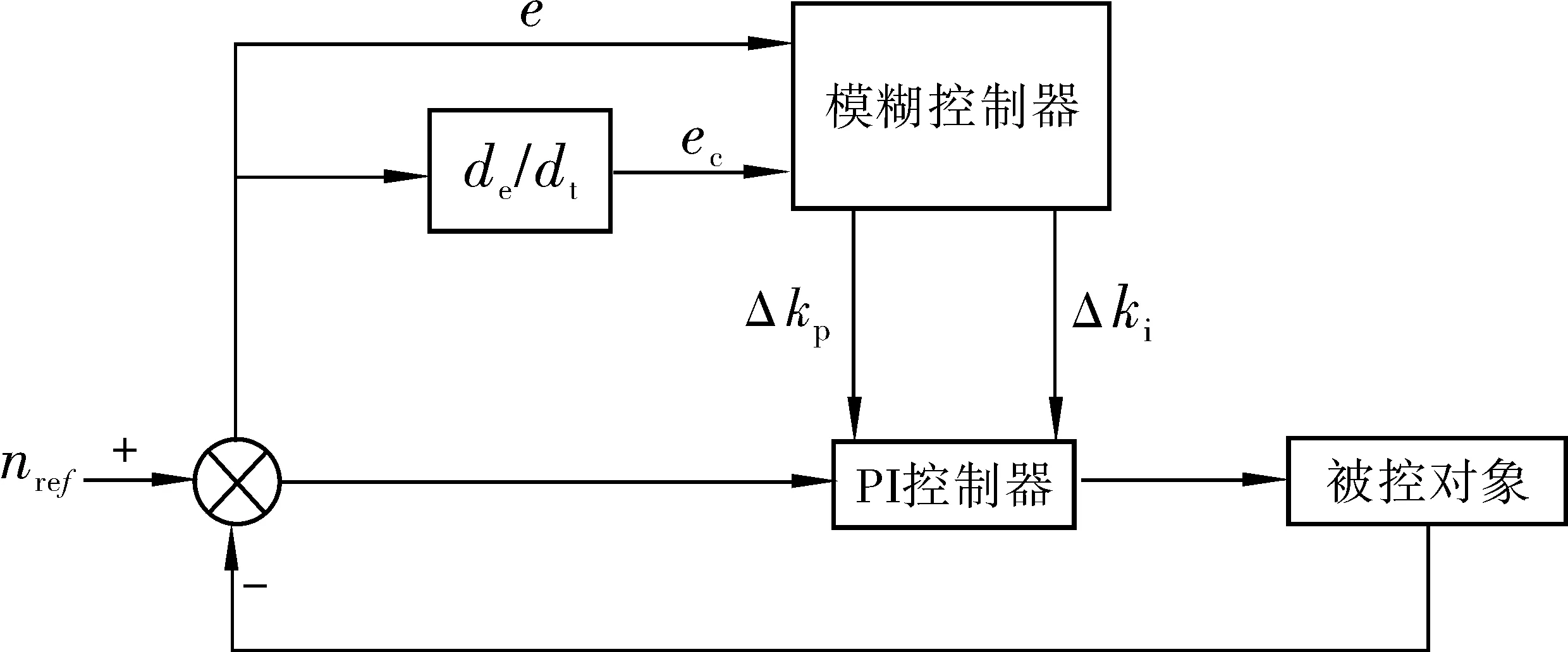
图2 Fuzzy-PI控制器原理Fig. 2 Principle of fuzzy-PI controller

合理设置模糊控制器输入变量的量化因子和输出变量比例因子及基本论域十分重要，对模糊控制器性能影响很大[12]。笔者根据实际调节经验和系统实际运行的动态范围，设置转速偏差e、误差变化率ec、比例系数修正值Δkp、积分系数修正值Δki的量化因子，基本论域，模糊论域，如表1。

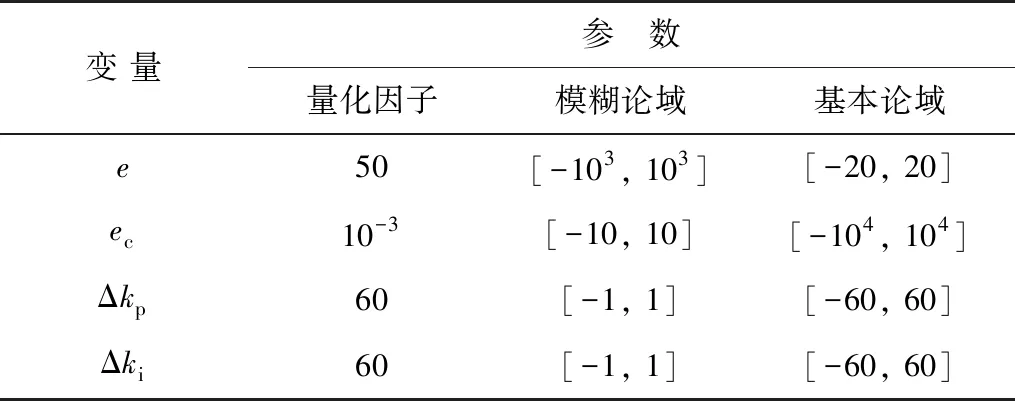
表1 Fuzzy-PI控制器参数设置Table 1 Fuzzy-PI controller parameter setting

对于输入输出变量的隶属度函数，笔者选取三角型隶属度函数，其计算工作量小，灵敏度高，且可以节省存储空间。e、ec、Δkp、Δki隶属度函数曲线如图3。

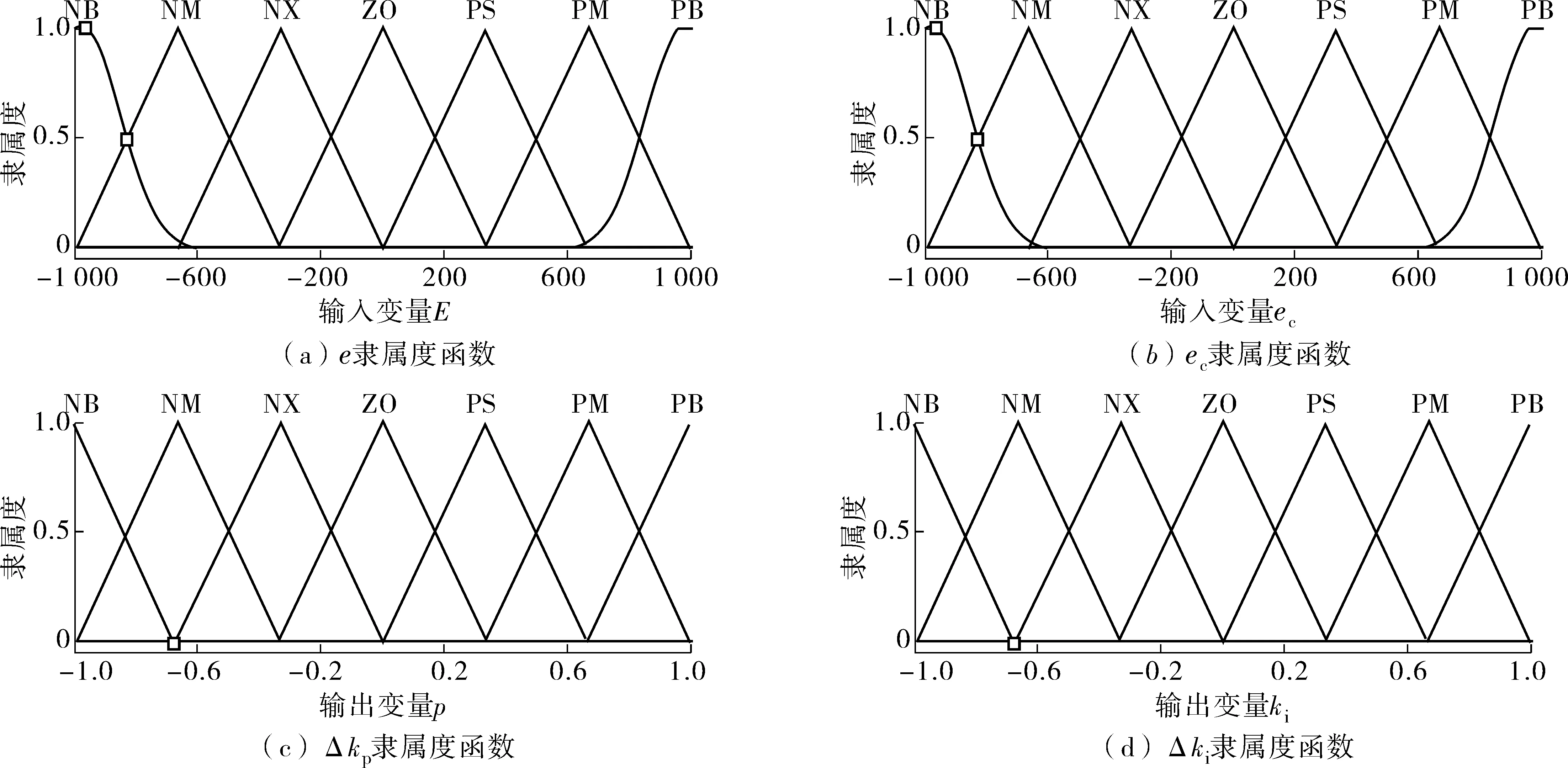
图3 隶属度函数Fig. 3 Membership function

模糊控制规则是模糊控制器的核心，根据人工专家经验和理论分析建立。依据 PI 参数调整经验和误差逐级逼近原则，建立Δkp和Δki的控制规则，笔者所建的Δkp和Δki模糊控制规则如表2、3。

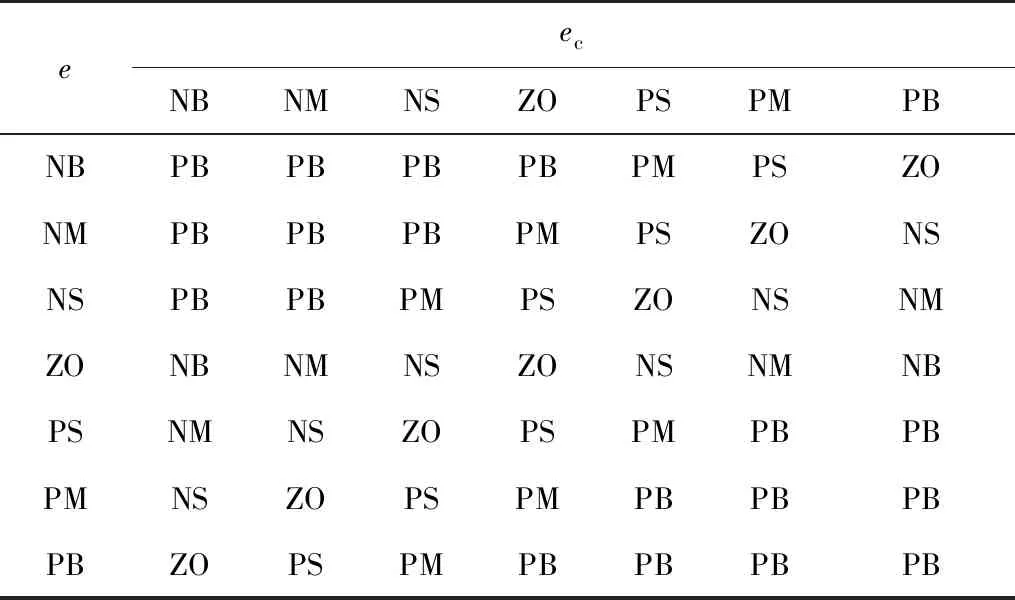
表2 Δ kp的模糊控制规则Table 2 Δ kp fuzzy control rule

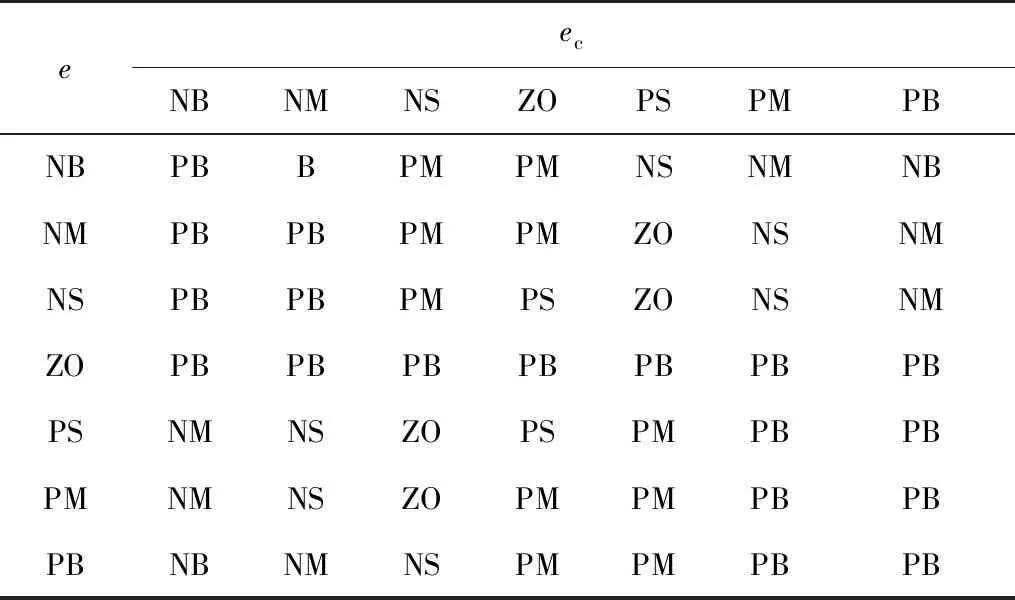
表3 Δ ki的模糊控制规则Table 3 Δ ki fuzzy control rule

表2、3中：NB(negative big)、NM(negative medium)、NS(negative small)、 ZO(zero)、PS(positive small)、PM(positive medium)和PB(positive big)分别表示负大、负中、负小、零、正小、正中和正大。根据表2、3中的模糊控制规则，并在Simulink中建立模糊控制语句如图4，共有49条推理语句。采用Mamdani方法得到模糊输出量，最终运用重心法进行解模糊，得到Δkp和Δki精确量。

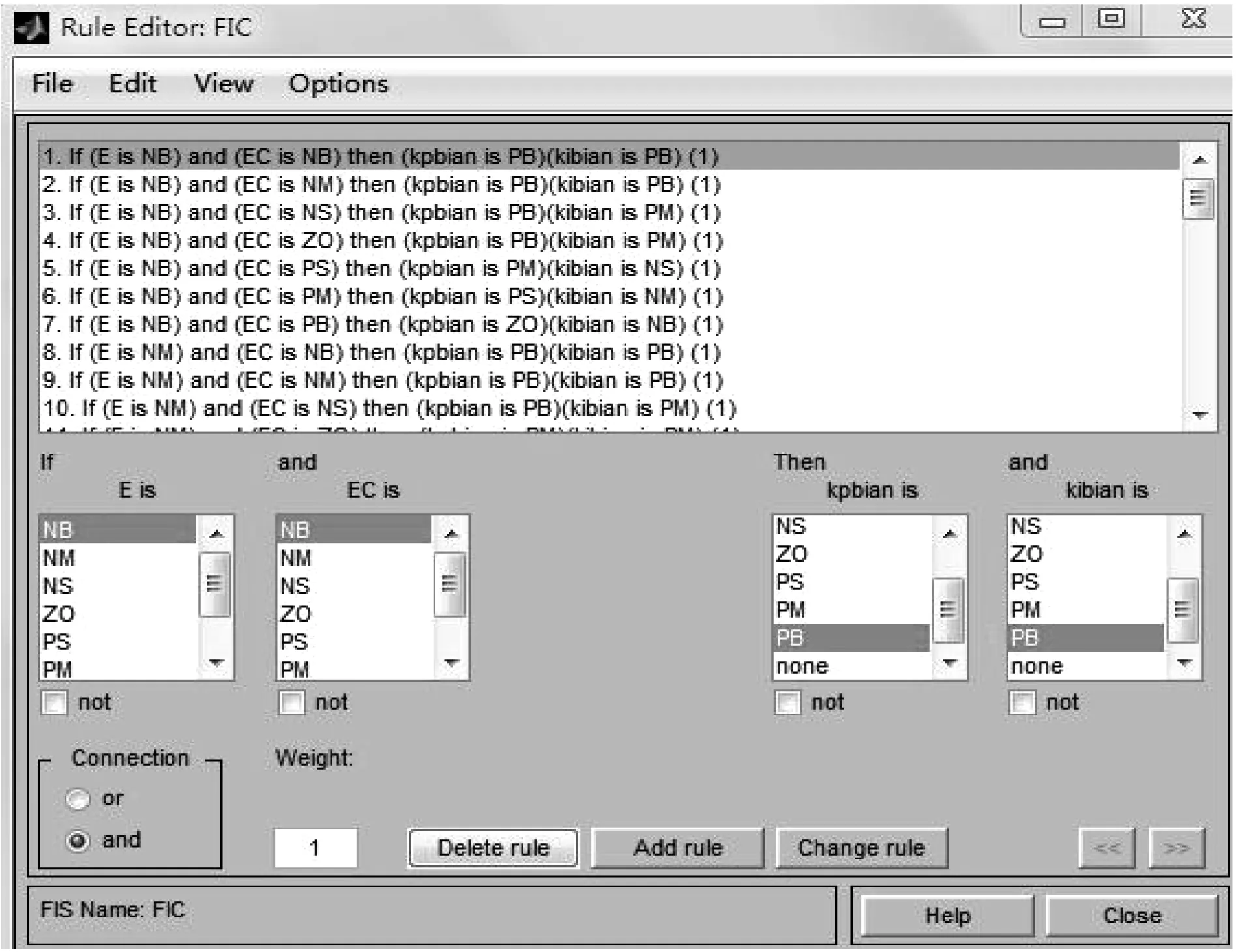
图4 Simulink中所建立模糊控制语句Fig. 4 Fuzzy control statement established in Simulink

3 控制系统仿真及结果分析

为验证Fuzzy-PI对IPMSM控制性能改善的有效性，基于Matlab/Simulink进行了IPMSM的MTPA和弱磁控制算法的调速模型建模，其转速环调节器分别采用固定PI和Fuzzy-PI控制器进行仿真对比。IPMSM仿真参数如表4。

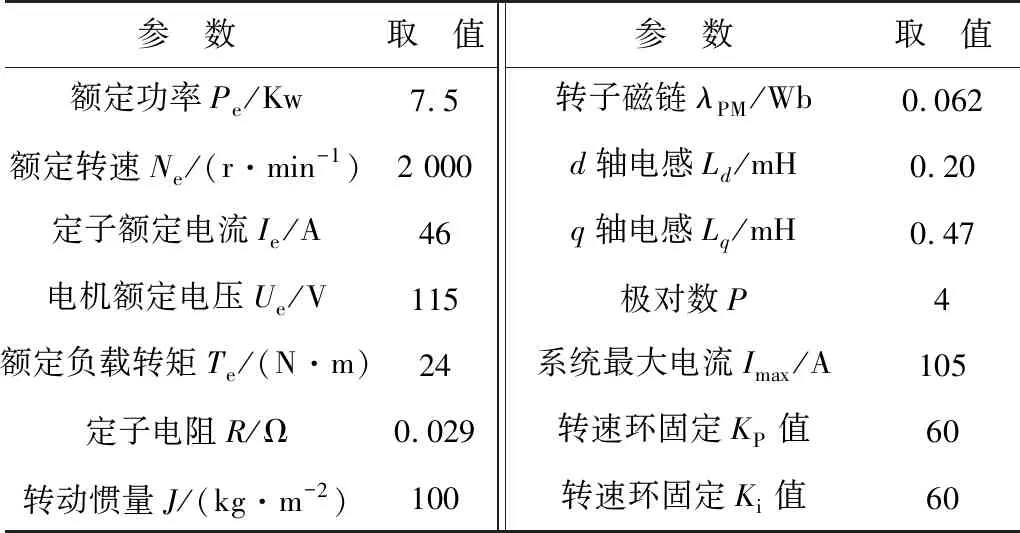
表4 IPMSM仿真参数Table 4 IPMSM simulation parameters

3.1 工况1

为测试IPMSM在系统状态不变，仅有指令转速变化时的全速度范围转速调节动、稳态特性，设定为工况1：负载转矩恒定为10 N·m，转速从0阶跃到高速转速6 000 r/min，0.35 s后转速下降到低速转速1 000 r/min。传统固定PI和Fuzzy-PI的电机转速跟随波形如图5、6。

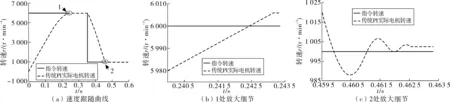
图5 固定PI工况1速度跟随曲线Fig. 5 Speed following curve under fixed PI condition 1

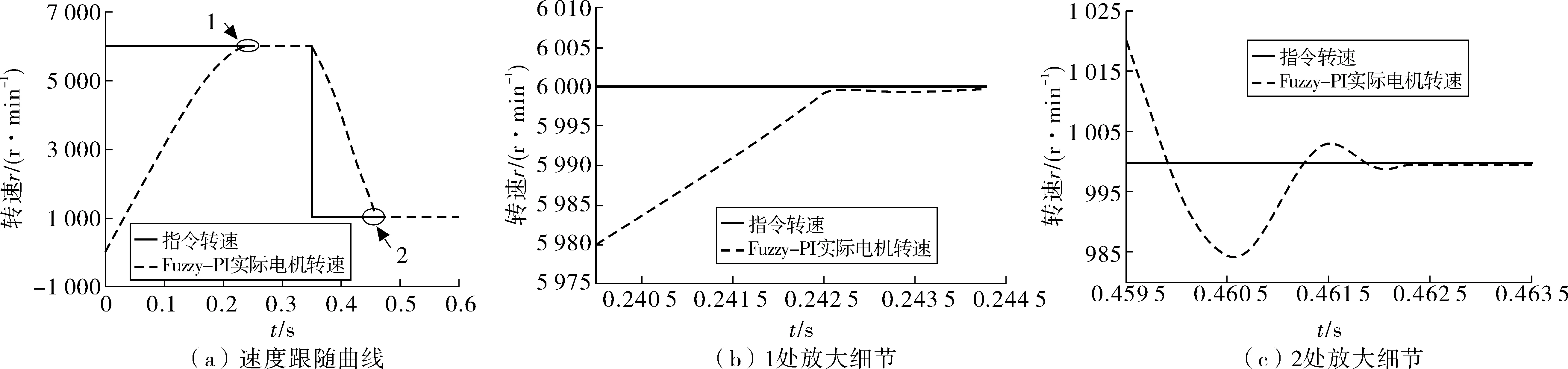
图6 Fuzzy-PI工况1速度跟随曲线Fig. 6 Speed following curve under fuzzy-PI condition 1

由图5(b)、(c)可看出：转速环采用传统固定PI时，当实际电机转速接近指令转速，由于PI参数固定不可调，全速度范围会出现超调振荡现象，且稳态静差均较大，同时指令转速越大，稳态静差也越大。

对比图5(b)、6(b)：指令转速为6 000 r/min时，固定PI的转速调节出现超调现象，转速稳定在6 006 r/min，稳态静差为6 r/min；而Fuzzy-PI转速调节未出现超调现象，转速平稳过渡并稳定在5 999 r/min，稳态静差为1 r/min。

对比图5(c)、6(c)：当指令转速为0.35 s时由6 000 r/min突变为1 000 r/min后，固定PI转速稳定在1 003 r/min，稳态静差为3 r/min；而Fuzzy-PI转速稳定在999 r/min，稳态静差为1 r/min。

3.2 工况2

为测试IPMSM转速调节对抗负载突变及参数变化等干扰鲁棒性，设定工况2：让IPMSM运行恒定转速1 000 r/min，0.04 s后负载转矩从10 N·m突变成30 N·m；0.05 s后负载转矩又从30 N·m突变成10 N·m。传统固定PI和Fuzzy-PI电机转速跟随波形分别由图7、8。

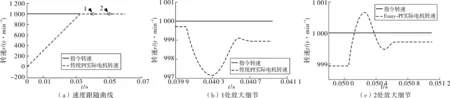
图7 固定PI工况2速度跟随曲线Fig. 7 Speed following curve under fixed PI condition 2

图8 Fuzzy-PI工况2速度跟随曲线Fig. 8 Speed following curve under fuzzy-PI condition 2

由图7(b)、(c)可看出：采用固定PI时，当负载转矩突变，转速会瞬间失稳，但很快经过调节就会恢复稳态，但调节过程震荡较大，过渡不平稳。

由图7(c)、8(c)可明显看出：在负载转矩突变增加或减小时，Fuzzy-PI相比固定PI，其恢复稳态超调振荡次数减少，过渡更为平稳。

3.3 工况1、2分析

由工况1结果可知：系统状态不变，仅有指令转速变化时，对于固定PI，在全速度范围内，其指令转速越小，超调振荡现象越严重，指令转速越大，稳态静差也不断增大。对比固定PI，采用Fuzzy-PI全速度范围超调震荡次数减少，稳态静差也大大减小，动、稳态性能及其响应速度都比固定PI均有明显的改善效果。

由工况2结果表明：在负载转矩突变扰动时，Fuzzy-PI相比固定PI具有更好动态性。

4 结 语

笔者在IPMSM伺服调速系统速度环中采用参数自整定Fuzzy-PI 控制器代替了传统固定PI控制器，并进行数值仿真。结果表明：在全速度范围，相比于传统固定PI控制器，参数自整定Fuzzy-PI控制器具有更好的动稳态性和鲁棒性，更能适应电动汽车运行特性。