主应力及其方向余弦计算的进一步研究

王 凯

(东南大学 交通学院，江苏 南京 210096)

0 引 言

在经典的弹性力学专著或教材中，均未给出主应力及其方向余弦的计算公式。在参考文献[1]和[2]中，笔者在前人工作的基础上，对3个主应力及其方向余弦的计算公式进行了详细的推导和阐述，而国外的一些著名的力学计算程序例如BISAR、ANSYS等，则利用计算方法中求解实对称方阵的全部特征值和特征向量的雅可比(Jacobi)方法，由应力矩阵计算出3个主应力及其方向余弦。这两种计算主应力及其方向余弦的方法在理论上有何联系，在各种力学状况下其计算结果是否一致，这是广大读者一直关心的问题。笔者拟对上述问题做进一步的研究和探讨。笔者曾阅读多本国内出版的弹性力学教材或专著，在这些教材或专著中，均未对两种方法的数学原理和计算过程作深入细致地介绍和论述，并通过计算对两种方法的计算结果进行对比和讨论。因此仅凭这些教材与专著中的内容，无法很好地回答上述读者所关心的问题。

1 特征值和特征向量的计算

1.1 特征值和特征向量的定义

由线性代数可知[3]，n阶方阵

的特征值是使方程组

(1)

即

(2)

有非零解的λ值。这个非零解(x1,x2,…,xn)即为该方阵的属于特征值λ的特征向量。

1.2 计算特征值和特征向量的第1种方法

根据齐次线性代数方程组有非零解的充要条件是系数行列式的值为零，特征值λ满足n次多项式方程：

(3)

展开方程(3)，即可进一步得到方程：

b0λn+b1λn-1+…+bn=0

(4)

方程(4)称为方阵A的特征方程，该方程的n个根(λ1,λ2,…,λn)即为方阵A的n个特征值。

由上述可得到确定方阵A的特征值和特征向量的第1种方法，该方法分成如下两步：

1)求解方阵A的特征方程(4)的全部根(λ1,λ2,…,λn)，得到全部特征值。

2)把所求得的特征值逐个代入方程组(2)，对于每一个特征值求解出方程组(2)的解(x1,x2,…,xn)，即可得到相应的特征向量。

由式(2)可知，如果(x1,x2,…,xn)是方程组(2)的一个非零解，那么(kx1,kx2,…,kxn)(k≠0)也是满足方程组(2)的非零解。这说明特征向量不是被特征值所唯一决定的。在实际应用问题中，往往对特征向量的取值加以“规格化”限制，即令所求算的特征向量值必须满足式(5)：

(5)

任意去掉方程组(2)中的一个方程式，并将剩余的(n-1)个方程式与式(5)联立求解，即可得到“规格化”的特征向量。该特征向量有两组解答，如其中一组为(x1,x2,…,xn)，则另一组为(-x1,-x2,…,-xn)。

1.3 计算特征值和特征向量的第2种方法

由线性代数和计算方法可知[3-4]，如果P为n阶非奇异方阵，P-1为其逆矩阵，则利用矩阵相乘相似变换(B=P-1AP)得到的n阶方阵B与n阶方阵A有相同的特征值。

实际中方阵A为实对称的情况较为常见，关于其特征值和特征向量的计算比一般情况要简单得多。线性代数理论表明，对于实对称方阵A,存在一个n阶正交方阵Q，使得：

Q-1AQ=D=diag(λ1,λ2,…,λn)

(6)

式中：λ1,λ2,…,λn为n阶方阵A的特征值；D为由n个特征值构成对角线元素的对角方阵。

n阶正交方阵Q的k列qk正好为n阶方阵A之相应于第k个特征值λk(k=1,2,…,n)的特征向量。

在计算数学中，雅可比方法是计算实对称方阵的全部特征值和特征向量的最常用方法。雅可比方法的基本思想是经过一系列正交变换(雅可比旋转变换)将n阶实对称方阵A一步一步化成由A的n个特征值构成对角线元素的对角方阵D，即：

(R1R2…Rm)-1A(R1R2…Rm)=D=diag(λ1,λ2,…,λn)

(7)

式中：R1,R2,…,Rm为旋转方阵。

与此同时，n阶方阵Q=R1R2…Rm为所有旋转方阵的乘积，其k列qk正好为n阶方阵A之相应于第k个特征值λk(k=1,2,…,n)的特征向量。

应用雅可比方法计算实对称方阵全部特征值和特征向量，已编成专用的计算机程序[5]。在该计算机程序中，考虑到实际应用的需要，一般还对所求的特征向量值规格化。因此当雅可比计算机程序计算结束时，即可得到实对称方阵全部的特征值和各特征向量平方和等于1的规格化特征向量。不过该特征向量解答不是全部解答，而仅仅是上述两组规格化特征向量解答中的一组解答。

2 弹性力学中主应力及其方向余弦的计算[6]

弹性力学中，求解主应力σ及其方向余弦(l,m,n)的方程组为：

(8)

又有：

l2+m2+n2=1

(9)

将式(8)和式(9)联立求解，即可得到σ,l,m,n的解答。齐次方程组(8)不能有l=m=n=0这样的解答，因为该解答与式(9)相矛盾。要使方程组(8)有别的解答，则必须取方程组的系数行列式等于零，即：

展开行列式得：

σ3-I1σ2+I2σ-I3=0

(10)

式中：I1、I2、I3为应力状态不变量，其值不随坐标系的改变而改变，分别为：

三次方程式(10)称为该应力状态的特征方程，它的3个实根σ1,σ2,σ3即为所求的主应力。运用一元三次方程的理论求解三次方程式(10)，即可得到3个主应力的计算式[1]：

(11)

与先前国内各种文献中出现的主应力计算公式相比，笔者所列的主应力计算公式无论是公式本身，还是在参考文献[1]中公式的推导过程都更完善，因而也更为学术界所接受。

由参考文献[6]，通过进一步力学分析，得到：

1)在弹性体内任意一点，一定存在3个相互垂直的主应力及其微分作用面(主平面)，主平面的外法线方向称为应力的主方向，主平面外法线的方向余弦与主应力的方向余弦相同。每一个主应力σi(i=1,2,3)及其主平面都是成对出现的。

2)在弹性体内任意一点，上述6个微分主平面构成一个微分六面体，同一个主应力的两个主平面相互平行，在其上分别作用着与其相对应的两个大小相等、方向相反的主应力。

由上述可知，弹性体内任意一点的每一个主应力σi(i=1,2,3)的方向余弦都有两组解答，如果其中一组是(li,mi,ni)，则另一组是(-li,-mi,-ni)。

在实际计算时求解主应力及其方向余弦，也有两种方法：

1)计算公式法

首先由前述的主应力计算式(11)即可计算出3个主应力，然后将所求出的3个主应力σi(i=1,2,3)依次代入式(8)中任意两式并与式(9)联立求解，即可得到相应的方向余弦li,mi,ni(i=1,2,3)。由式(8)和式(9)可知，与σi相对应的方向余弦有两组解答，如果其中一组为(li,mi,ni)，则另一组为(-li,-mi,-ni)，这与上面的力学分析一致。

由于参考文献[2]已将主应力方向余弦的计算公式推导出，因此在实际计算时，可直接利用该计算公式计算主应力方向余弦。由参考文献[2]可知，该文中主应力方向余弦的求解只列出正数解的表达式，因此采用该文中公式仅计算了两组主应力方向余弦解答中的一组解答。不过一旦该解答li,mi,ni(i=1,2,3)得到后，另一组解答(-li,-mi,-ni)也很容易得到。

2)雅可比方法

如果将式(8)改写成：

(12)

由式(12)即可看出主应力σ是应力矩阵S的特征值，应力矩阵S如式(13):

(13)

主应力方向余弦为应力矩阵S的属于特征值σ的特征向量。因此，可以利用计算方法中求解实对称方阵全部特征值及其相应规格化特征向量的雅可比方法及相应的计算机程序，计算出全部主应力和主应力方向余弦。如前所述，采用该方法只能计算出两组主应力方向余弦解答中的一组解答。与计算公式法一样，一旦该解答li,mi,ni(i=1,2,3)得到后，另一组解答(-li,-mi,-ni)也很容易得到。

3 计算算例

在笔者编写的NESCP程序[7]中，计算主应力及其方向余弦采用计算公式法，而在BISAR程序[8]中则采用雅可比方法。作者利用上述两个程序计算了各种应力状况下的几十个算例。由于篇幅有限，仅列出其中4个算例，如表1、表2、表3。每个算例中NESCP程序的计算结果精确到4位有效数字， BISAR程序的计算结果精确到3位有效数字。

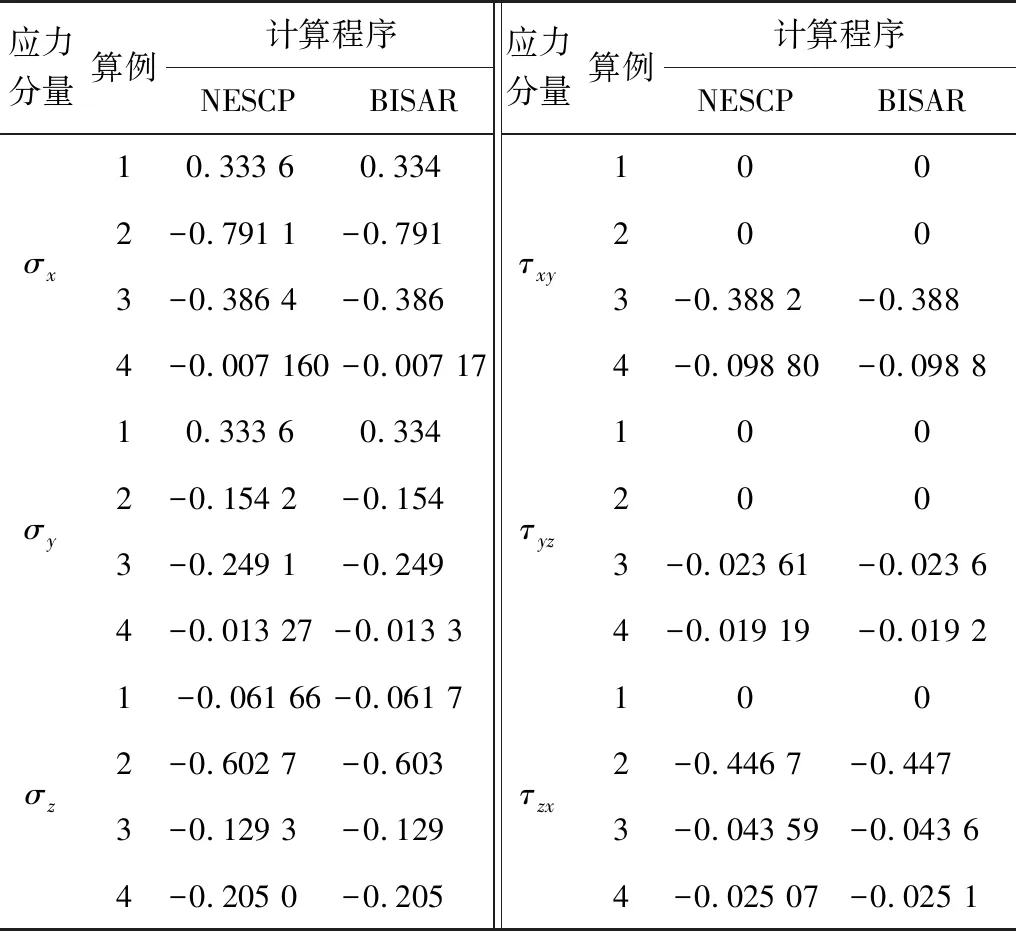
表1 算例1～算例4应力分量计算结果汇总Table 1 Summary of calculation results of stress components in example 1～example 4 MPa

表2 算例1～算例4主应力及其方向余弦计算结果汇总Table 2 Summary of calculation results of principal stresses and their direction cosines in example 1～example 4

表1、表2的计算结果表明，利用两个程序得到的主应力的计算结果十分接近；主应力方向余弦的计算结果则分两种情况：一种情况是计算结果的绝对值十分接近，符号也相同，另一种情况是计算结果的绝对值十分接近，而符号相反。由前面所述可知，两种计算方法实际上均只计算了两组主应力方向余弦解答中的一组解答[假设该解答为li,mi,ni(i=1,2,3)]，如果将另一组解答(-li,-mi,-ni)补齐，则由表3[表3中的计算数据在表2中算例4主应力及其方向余弦计算数据的基础上将另一组主应力方向余弦解答(-li,-mi,-ni)补齐后得到] 可知，在此情况下，不仅主应力的计算结果十分接近，每一个主应力方向余弦的计算结果也十分接近，仅计算结果中主应力方向余弦的排列次序可能不一样。

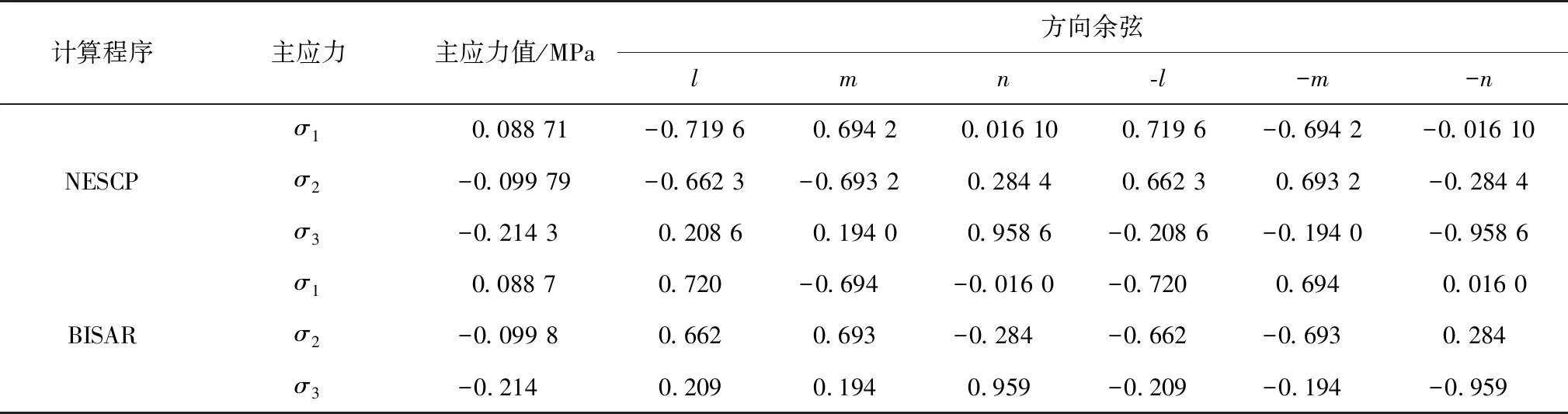
表3 算例4主应力及其方向余弦完整计算结果Table 3 Complete calculation results of principal stresses and their direction cosines in example 4

4 结 论

综上所述，可得到如下结论：

1)弹性力学中计算主应力及其方向余弦的两种方法即计算公式法和雅可比方法与线性代数中计算特征值及其特征向量的两种方法一脉相承，或者说弹性力学中计算主应力及其方向余弦的两种方法具有相同的数学渊源。

2)弹性体内任意一点的每一个主应力σi(i=1,2,3)及其主平面均成对出现。同一个主应力的两个主平面相互平行，在其上分别作用着与其相对应的两个大小相等、方向相反的主应力。因此每一个主应力σi(i=1,2,3)的方向余弦都有两组解答，如果其中一组解答为(li,mi,ni)，则另一组解答为(-li,-mi,-ni)。目前采用计算公式法或雅可比方法计算主应力方向余弦，实际上均只计算了两组主应力方向余弦解答中的一组解答，只有将另一组解答补齐，才能得到完整的计算结果。

3)计算表明，在各种力学状况下上述两种方法的计算结果十分接近，仅计算结果中主应力方向余弦的排列次序可能不一样。无论是采用计算公式法还是采用雅可比方法均能得到足够精确的主应力及其方向余弦的计算结果。

由上述结论可知，笔者的研究成果不仅很好地回答了读者的问题，也是对经典的弹性力学基础理论做了一点很好的补充。

致谢：笔者对东南大学数学学院赵业鑫副教授的帮助谨表示衷心感谢。