在运算教学中渗透思维训练——“20 以内的退位减法”单元教学设计与评析

◇设计/周 志 评析/胡重光

一 运算方法的选择

“20 以内的退位减法” 是一年级下册教材（人教版）的教学内容，教材中介绍了两种运算方法。以15-9 为例。一是把被减数分成10 和5，用10 减去9 得1，再将1 加5 就得6 （通常叫作“破十法”）。二是利用减法是加法的逆运算：因为9+6=15，所以15-9=6(通常叫作“想加算减”)。这两种方法各有什么优点或不足，教材中没有给出评价，只是在练习中说明 “用你喜欢的方法计算”。其意图显然是：不必分出优劣。

这两种方法差别很大，令人觉得有必要对其进行对比和分析。

第一种方法的思路是设法简化运算，将复杂的新运算转化为已经学过的简单运算。第二种方法则没有做减法，而是做了一道加法题，再根据减法是加法的逆运算，直接得出减法的结果。第一种方法是化繁为简，分步计算,没有新的思维方式。第二种方法则包含两种新的思维方式：

第一，这种方法把加法和减法这两种不同的运算联系了起来。 用联系的观点看问题对于儿童的学习极为重要。 曾任美国联邦教育署长的当代著名教育家欧内斯特·L·博耶曾引用马克·范·多琳（Mar

k Van Doren）的话：“找出各种事物之间的联系是教育家们竭尽全力思考的问题……当学生能够用相互联系的观点看待各种事物的时候，他们的学习生涯就开始了。我建议把发现事物之间的联系当作基础学校（即小学——引者注）课程的首要目标。”[1]

第二，这种方法利用了逆运算。这一点也很重要。 美国数学教育家J·W·海敦斯教授指出：“逆运算概念是基本数学结构的一个重要概念，它对理解初等数学是必须的。”[2]

随之而来的问题是，一年级的学生能否理解和运用第二种方法包含的思维方式呢？

事实上，在一年级上册的教材中已经使用了第二种方法包含的思维方式。例如，教材（人教版）在第53 页安排了这样的练习：

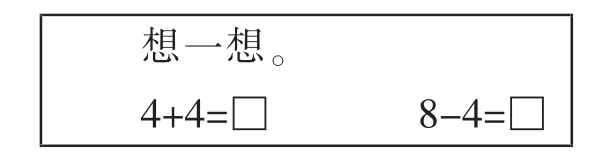
图1

还出现了许多如图2 所示的“分与合”的问题：（第21 页）

图2

这类问题也包含逆运算思维。

经过这两类问题的学习，儿童应该对加法和减法之间的联系有所认识，初步具备了根据逆运算的关系“想加算减”的能力。因此，选择第二种运算方法是顺理成章的。

二 运算方法的教学

（一）感悟。

让学生进行以下两个操作活动。

活动1：凑数游戏。同桌两人玩，每人准备十几根小棒（或扣子、围棋子等）。双方约定一个要凑的数（教师要求最好是十几），比如15。然后由甲方拿出几根小棒（少于15 根）摆在课桌上；再由乙方出小棒，所出小棒与桌上的小棒加起来要恰好等于15。如果出对了，那么桌子上的小棒都归乙；如果出错了，则桌子上的小棒都归甲。

活动2：猜数游戏。也是同桌两人用小棒玩。先拿出十几根小棒摆在桌子上，接着甲从中拿走若干根，但不让乙看见是几根；然后乙要根据桌子上剩下的小棒猜出甲拿走了几根。 猜对了，则剩下的小棒都归乙；猜错了，就都归甲。

这两个活动的目的是让学生通过实物操作来感悟加法和减法的关系及逆运算概念，既可复习20以内的进位加法，又可为“想加算减”的方法打下基础。采用实物操作，并设计为游戏活动，符合处于具体运算阶段的儿童的认知特点，具有较强的趣味性。

（二）内化。

前面的两个活动都是通过操作实物进行的，学生的认知依赖于具体事物，所获得的知识是经验型的。 因此还需经过内化形成系统的理论知识。内化活动可通过以下两个层次的练习进行。

1.笔算。让学生进行以下各类运算：

（1）7+8=15 15-7= 15-8=

5+9=14 14-5= 14-9=

……

（2）11-7=4 11-4= 7+4=

13-5=8 13-8= 5+8=

……

（3）15-9=6 15-□=9 □+6=15

12-4=8 12-□=4 □+8=12

……

（4）6+5=11 □-5=6 □-6=5

8+4=12 □-4=8 □-8=4

……

这些计算要求学生独立完成，但可以操作小棒等学具或利用数轴辅助计算。如果发现学生出现错误，教师可以引导他们通过操作学具来发现和纠正。通过大量各种类型的题目的计算，儿童最终完成减法是加法的逆运算的知识建构。

2.口算。由同桌两人合作进行，一人出题，另一人回答。每次练习以上四组题中的一组，出题人从自己的笔算题中随机抽取题目。例如，先约好做第二组题，甲先报“11-7=4”，然后问“11-4等于几？7+4 等于几”，乙回答时，不能看自己的笔算答案。回答正确，甲给乙一件奖品（小星星、小红旗之类，由教师先发给每名同学）。二人轮流出题、答题，四组题都练完后，看谁的奖品多。

三 思维的拓展

（一）整理。

教师将表1（教材一年级下册第24 页）发给每一名学生：

表1

学生将表1 填完整，得到20 以内的全部退位减法算式，如表2。

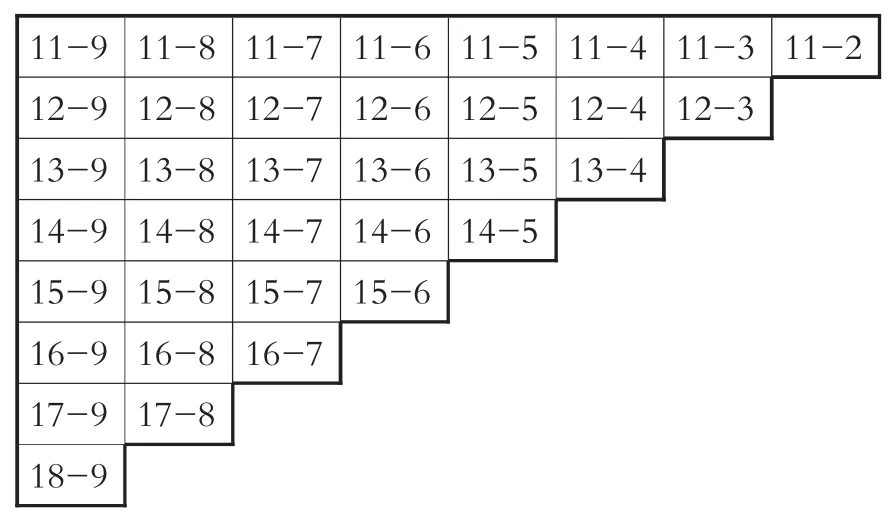
表2

在这里，看起来学生只做了简单的填表工作，与运算似乎没有什么关系。但是这种表将20 以内的退位减法做了有序排列，形成了结构，这可能会对学生以后的成长发挥很大的作用。 伟大的哲学家、数学家笛卡儿说：所谓方法，就是把我们应注意的事物进行适当的整理和排列。可见，笛卡儿将这一工作作为了所有科学研究最基本的方法。因此，从小学开始，我们就应该训练学生掌握这种方法，并引导他们自觉地运用这种方法。

（二）计算。

学生计算表2 中的每一个算式，并将结果填入表中（如表3）。

表3

（三）找规律。

引导学生横着、竖着仔细观察表3，找出其中有规律性的联系。学生自由发言，先在小组里说，然后各组派代表说出本组的发现。 一年级的学生表达能力不强，教师可以让他们尽量用算式表示。在学生充分发言后，教师归纳出以下规律：

1.竖着看。从第一列（减9）可以发现：11-9=1+1，12-9=2+1，13-9=3+1，…，18-9=8+1，即差总是比被减数的个位大1； 再让学生观察第二列（减8），又可发现：差总比被减数的个位大2；以此类推。

（2）横着看。从第一行（11 减几）可以发现：11-9=1+1，11-8=2+1，11-7=3+1，…，11-2=8+1，即差总等于减数的补数 （减数的补数指10 减去减数所得的数）加1；再让学生观察第二行（12 减几），又可发现：差总等于减数的补数加2；以此类推。

掌握了这两条规律，就可以很快地写出表中任意一个减法算式的结果。 这两条规律是通过把20 以内的全部退位减法算式按一定的顺序排列起来而发现的，如果我们单个地或分开来教学，就不容易发现。

四 应用

学习运算的主要目的是解决现实问题。因此，最后我们应当提供一些应用题让学生解答，这些题目应真正具有现实背景。例如：

学校举行跳绳比赛，小强取得第11 名，小亮的名次比小强高3 个，小亮得了第几名？

小明与小红住在同一个单元，小明住在2 楼，小红住在11 楼，从小明家到小红家要上几层楼？

昨天的最高气温是14℃，今天的最高气温是8℃，今天的最高气温比昨天低几度？

公共汽车到站时下了4 人，上了12 人，车上的人是多了还是少了？多了或少了几人？

东东把零用钱存起来准备买一本定价为15元的书，他已经存了9 元，还差几元？

还可以插入几道20 以内的进位加法应用题，以免学生形成思维定式，例如：

学校举行跑步比赛，小强取得第9 名，小亮的名次比小强低3 个，小亮得了第几名？

电梯从1 楼开始，先上了8 层楼，接着又上了5 层楼，现在电梯在几楼？

小明今年7 岁，大牛比小明大4 岁，大牛今年多少岁？

【评析】

我们通常比较注意单个课时的教学设计。其实，教材中的内容一般是按单元分块的，单元是教材的基本结构，具有相对的独立性和整体性。进行单个课时的教学设计前，应首先进行单元的整体教学设计，单个课时的教学设计应以单元的整体教学设计为基础。

运算教学最忌为计算而计算，脱离思维训练，脱离现实应用，结果学生只获得一点干巴巴的计算技能。本设计最大的特点是注重思维训练，不但在运算方法的选择和教法上体现了这一点，而且专门安排了“思维的拓展”和“应用”两个环节。

本设计的关键环节是活动1 和活动2。这两个活动让学生通过实物操作感悟数量关系，具有形象性和具体性，符合儿童的认知特点和心理规律。起初学生可能算得慢，甚至需要数小棒，教师不要操之过急，应给学生充分的时间进行活动。通过大量的练习，学生会越来越熟练。通过这两个活动，应该使学生达到脱口而出的熟练程度。有了这两个活动作为基础，学生就能顺利完成后面的笔算练习。

让学生观察有序排列的算式表，找出其中的规律，能培养他们的数学观察能力。通常认为观察主要用于物理、化学、生物等自然学科之中，因而在数学教学中很少提及。其实，在数学中观察也是重要的基本能力。 法国著名数学家埃尔米特就曾指出： 科学的历史广泛地证实了一个简单的事实，即在数学家的思维过程中，观察占有重要的地位，并且起着巨大的作用。

“应用”这一环节列出了许多应用题，这些题都具有儿童熟悉的现实背景。这一点具有重要意义。弗赖登塔尔奖获得者梁贯成教授介绍的一项数学调查生动地说明了这一点。（如表4）

表4 5个小学生的计算测试结果