注重表征 凸显本质
——听罗鸣亮老师教学“小数的意义”一课有感
◇徐文艳
在一次研讨会上有幸聆听了青年名师罗鸣亮老师设计和呈现的“小数的意义”一课,受益良多。
【课堂回顾】
一、复习“十进制”,明确小数产生的必要性
1.复习整数“十进制”。
师:我们从一年级开始就学习数数。 老师这里面有涂色的正方形,我们一起来数一数有几个。
(师出示涂满颜色的正方形,学生一个一个地数)
师(小 结 ):10个一就是10,如果10 个10 个地数,10 个 十 就 是100,10 个百是1000 ,都是满十进一。
2.明确小数产生的必要性。
师:我们再来数。
(师出示图1)

图1
师(追问):为什么不用整数表示呢?
(生答略)
师:是的,人们在计量物品的时候,常常不能正好得到整数结果,这时可以用分数或小数表示。(板书:小数)这节课我们一起来进一步认识小数。
二、认识小数
1.认识一位小数。
师:涂色的部分,同学们猜得对不对,有什么好办法可以判断?
[学生想办法证实自己的猜测。 猜测结果为小数(0.7 或0.8)的学生都能想到:把这个正方形平均分成10 份,看看涂色的部分占其中的几份]
师:为什么平均分成10 份?
从而引导学生理解计数单位“0.1”,得出:1 平均分成10 份→()→0.1。从而得出正确答案为0.7。
师:如果老师信封里的正方形上涂色的有4 块,你们猜这个数是多少?
(学生不约而同地说出0.4。老师呈现涂色正方形,如图2 所示)
生:既然是小数,应该平均分成10 份,这里平均分成了5 份,应把这5 份再平均分,变成10份,那么原来的4 份就成了8 份,是0.8。

图2
(老师根据学生的回答,通过电脑课件演示:把5 份再分变成了10 份。并带着学生一起数: 1个0.1,2 个0.1……8 个0.1,是0.8)
2.认识两位小数。
师:还要继续猜吗?需要什么提示吗?
(学生表示:平均分成了几份,涂了几份)
师: 接下来这个正方形平均分成10 份了,不过,涂色的比8 份多。
(大部分学生表示应该是: 0.9 或1,并说明理由)
师:谁说得对呢? 请看,如图3 所示。
[学生猜测是0.88,并想办法证实自己的猜测:把0.1(第9 份)再平均分成10 份,每一小份是0.01,然后数一数里面有几个0.01。教师课件演示学生的想法,并得出板书: 0.1 再平均分成10 份→()→0.01。接着,继续通过正方形模型认识两位小数0.89、0.90]

图3
3.认识三位小数。
师:在这个正方形中怎么表示出0.536 呢?
(教师根据学生回答,课件同步演示两种想法,如图4 所示。学生在交流、说理中认识了计数单位“0.001”及三位小数)
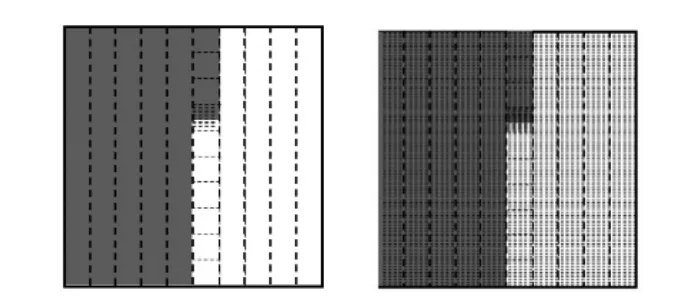
图4
三、借助数轴模型,进一步理解小数
教师把方格图进行动态演变,逐步展开为长图(如图5 所示),让学生先感受出0.536 的位置,并在数轴(如图6)上一起寻找1.73 的位置。
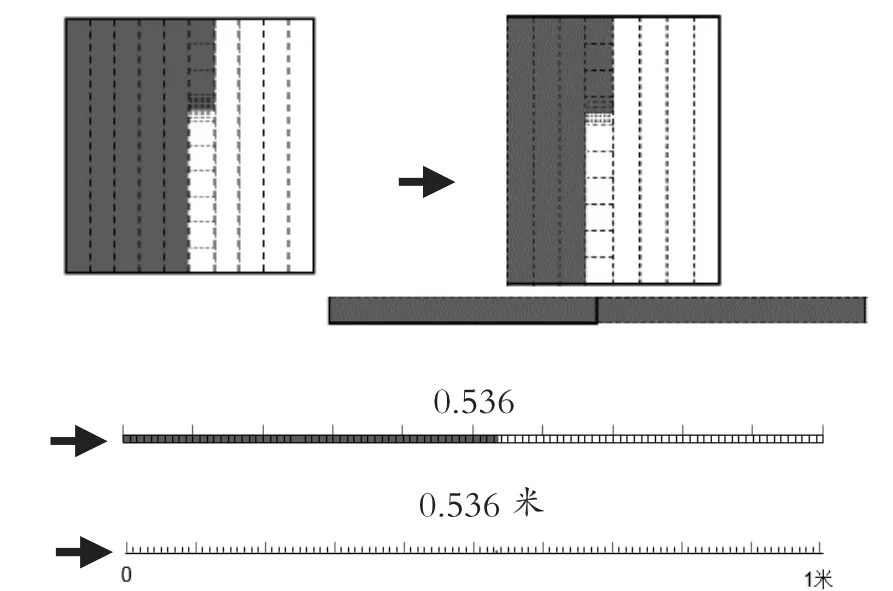
图5

图6
【课后感悟】
一、注重表征
1.选择正方形模型,引导学生主动建构。
在小数的意义教学中,单纯借助分数来理解小数的十进关系有一定的难度。教师常常会选择和运用正方形、正方体等直观模型图,去帮助学生建立清晰的小数概念。罗老师是选择了正方形模型,我认为对于四年级的学生来说更合适。因为正方形比正方体模型更直观,更利于引导学生自我建构小数的含义。
罗老师犹如一位高明的魔术师,给正方形模型进行着色“加工”,每一次呈现的面积模型都是精心设计的,承载了不同的用意。
课堂中呈现的第一个色块图(图1):先让学生明确小数产生的必要性,接着让学生在“猜测、说理”中着重理解计数单位“0.1”;并引导学生根据示意图一起数出小数 “1 个0.1,2 个0.1……7个0.1,10 份里的7 份,是,也是0.7”,形象地解释这些一位小数都是由“0.1”这个计数单位累加起来的。
第二个色块图(图2)可谓是一个“圈套”:引诱学生往里钻,当学生发现4 份不一定就是0.4,而要看有没有把1 平均分成10 份时,一位小数的意义在学生的交流中得以凸显。
而在第三个色块图(图3)呈现之前,罗老师巧妙利用了学生的思维定式“接下来这个正方形平均分成10 份了,不过,涂色的比8 份多”。学生都认为答案不是0.9 就是1。可当第三个色块图呈现出来之后,出乎孩子们的意料,但一切又在情理之中。此时,学生发现用一位小数已无法表示出时,自然地产生了将0.1 平均分成10份的需要。在平均分的过程中,学生也直观地理解了计数单位“0.1”和“0.01”之间的联系,从而实现了从一位小数到两位小数的“无痕”过渡。
而在三位小数的认识过程中,教师大胆放手,让学生用正方形模型在头脑中画出“0.536”。学生有了前面的认知经验,自然而然可以想到两种表示方法: (如图4)
一是,把一个正方形先平均分成10 份,涂其中的5 份,表示0.5;再把第六份平均分成10份,涂其中的3 份,表示0.03; 然后把第六份里面的第四小份再平均分成10 份,相当于把正方形平均分成1000 份,每一份是0.001,涂其中的6 份,表示0.006。 二是,把一个正方形平均分成1000 份,涂其中的536 份。
教师借助直观图引导学生沟通两种方法间的联系,让学生在自主讨论、辨析中明晰三位小数的意义。伴随着直观图的“演变”与呈现,学生实现了数概念的主动建构。
2.运用数轴模型,引领学生深层理解。
通过把面积模型动态转变为线型模型,让学生初步理解数轴上的点是稠密的,并且是连续的; 在此过程中也让学生接触了整数部分不是0 的小数,避免了小数就是零点几的消极思维定式,实现了对小数意义的进一步理解。
二、凸显本质
1.关注小数与整数的联系。
小数其实是“采用整数位值原则书写的十进分数”,但老师们对小数与整数的联系似乎都不怎么关注,我发现罗老师很好地关注了这一点。
罗老师先与学生一起复习整数的计数单位及其进率,从低位到高位是“十进”;进一步,罗老师通过创设情境,并结合正方形直观图的演示引出从左往右是“十分”。并在交流过程中形成以下的板书:

学生通过本节课的学习深深感受到:小数并不是分数改写而产生的,而是不断细分的结果,是自然数的十进位值制从高位往低位扩展的结果。
2.理解小数和分数的关系。
小数与分数的关系如果仅仅停留在“一位小数表示十分之几,两位小数表示百分之几……”这些抽象的概念语言上,显然没有从本质上完成概念的建构与理解。
罗老师此节课借助长方形这一模型,通过猜测、说理、辨析,着力让学生明白:一位小数就是把一个整体平均分成10 份,表示这样几份的分数……理解有限小数就是特殊的十进分数这一本质。整节课处处彰显着这一点,在此举两个环节加以阐述。
有一个环节让笔者记忆尤为深刻: 罗老师创设了 “如果老师信封里的正方形上涂色的有4块,你们猜这个数是多少”的问题情境。引诱学生往里钻,当学生发现4 份不一定就是0.4,而要看有没有把1 平均分成10 份时,一位小数的意义得以再次凸显: 一位小数就是把一个整体平均分成10 份,表示这样几份的分数。
再如,认识两位小数时,当学生说出“0.9”和“0.90”都可以表示正方形涂色部分后,老师追问:“为什么有的时候是一位小数,而有的时候是两位小数呢?什么原因?”学生在交流中明晰了小数和分母为10、100 的分数有关系。

