透视核心概念 溯源数学本真——《小学数学教材中的大道理——核心概念理解与呈现》研读与感悟

◇刘爱东

《小学数学教材中的大道理——核心概念的理解与呈现》一书由华东师范大学张奠宙教授和杭州师范大学巩子坤教授等著（以张教授在本刊所发“评论与建议”文章为主——编者注）。之所以取这个名字，是因为“虽然小学数学的学习难度不大，但它背后所依靠的道理并不小”。书中内容紧紧围绕数学核心概念的理解，就目前课程标准和小学数学教材中“有所欠缺的”“一些流传很广的认识和表述”，或从知识的滥觞处追根溯源，或从数学的本真处正本清源，或从教学的实际应用中辩证厘析，鞭辟入里、以理服人，其最终目的在于通过对小学数学核心概念的深度剖析，经由教师的教学“让孩子们获得更好的数学素养”。既有专家居高望远的引领，又有根植教学一线的实证相佐，是一本不可多得的好书。

一 追根溯源，立足数学历史大空间

数学发展史告诉我们：一个个体的发育史会重蹈其种族的发展史。 其表现在数学学习中，就是学生学习数学的认知过程与数学史的发展过程相似。为了厘清概念本质、促进学生发展，张奠宙教授十分注重从数学文化的高度，用数学发展的眼光引导教师开发教材，推陈出新。

在读到对于“方程”概念的表述时，张教授从“方程”一词的来源进行数学史的考证，发现该词在西方是没有的，西方只有“等式”。该词来源于《九章算术》中的解线性方程，“方”是指把线性方程组的系数排列成一个方阵，“程”的意思是按照一定的程式进行运算，最后把未知数找出来，两个字合起来意为系数按照一定的程式进行运算的过程，而非教材上所定义的“含有未知数的等式叫方程”。 因此，他建议教材要淡化方程的定义。他认为，学习方程的关键在于“理解方程思想的本质以及它的价值和意义”，而方程的本质是“为了寻求未知数，在未知数和已知数之间建立起来的相等关系”，其核心价值是“为了寻求未知数”。这样的分析有理有据，对于一直被“x＝1 是不是方程”折腾的一线教师而言，无疑具有十分重要的指导意义，因为x＝1 中未知数是几已经很清楚了，无须再去“寻求”，而且没必要进行这种毫无意义的自我折腾。

有了这样全新的认识，教学中，我改变传统教学中着重于以“含有未知数”“等式”为重点的定义，而是围绕“为了寻求未知数，在未知数和已知数之间建立起等式关系”这一方程思想重构教学过程，数学价值更加凸显。具体分三步：

第一步，通过认识已知数和未知数让学生明白，今天的学习是研究未知数和已知数之间的一种特殊关系。

第二步，在已知数和未知数间建立关系。给出一组已知数和未知数之间的数量关系，如x－30＜108、x－20＞108、x－25＝108 等，让学生明白，其中能帮助我们获得未知数值的，即有“等量关系”存在的，叫作方程。

第三步，丰富内涵理解方程。借助天平，在天平的左边放两个梨，右边放3 个苹果，天平平衡。问：你能根据“2 个梨的重量＝3 个苹果的重量”这个等式，分别知道每个梨和每个苹果的重量吗？

引导学生明白，仅有等量关系不一定能够获得未知数的值，仅有已知数也未必能获得未知数的值，只有在未知数和已知数之间建立等量关系，并能借助已知数和等量关系获得未知数的值，这样的等量关系才是方程。

二 关注本质，基于教学逻辑大视野

交换律的本质是什么？为什么两个加数（乘数）可以交换？怎样的教学过程才能反映出交换律的本质？在阅读本书之前，虽然也有相关思考，但一直以来离不开“两个加数（乘数）交换位置，和（积）不变”的概念定义。

张教授在书中告诉我们，理解加法交换律应该基于加法的意义，“加法的本质是接着数，它来自于添加或合并的操作活动”。 这样的论述让我明白了“交换两个加数”意味着两个求和的过程是两个不同的数数过程，如5+8 与8+5，前者是以5 为基础接着往下数8 个，后者是以8 为基础接着往下数5 个，虽然结果相同，但数的过程是有区别的，而这正是加法交换律的本质所在。同样的，乘法交换律源于乘法的意义，即“求几个相同加数的和的简便运算”，以此得知，3×5 和5×3也是两个不同的数数的过程，前者是3+3+3+3+3，数5 个3，而后者是5+5+5，数3 个5，虽然结果相同，但计算的过程是有区别的。

借鉴上述观点，我在教学中作了一些改变与尝试。比如，乘法交换律的教学，我把教材上踢毽子图（如图1）稍作改变，改成每排5 人，共3 排。引导学生据图交流得出，横着数，每行5 人，3 行共有5×3＝15（人）；竖着数，每行3 人，5 行共有3×5＝15（人）。因为结果都是15 人，所以有5×3＝3×5。这样的设计，从乘法的意义出发学习乘法交换律，打破了学生普遍通过机械记忆的方法学习乘法交换律的困境。

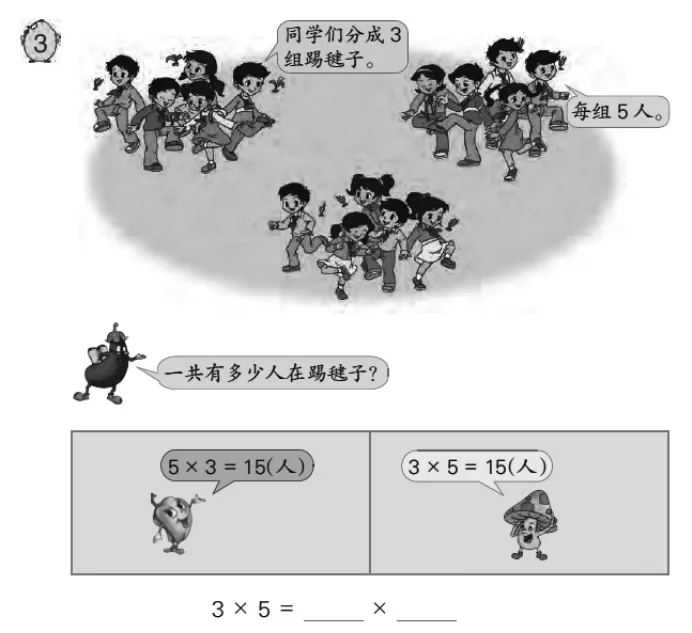
图1

像这样从数学逻辑大视野的角度厘清知识脉络关系，引导学生建构知识体系的例子，在书中还有很多。它昭示我们，小学数学并不小，只有从数学的本质出发，才能基于追寻数学根部知识，在引导学生不断体验数学方法、感悟数学思想中，有效建构数学知识体系，实现数学学习过程即知识自然生长过程的教学目标。

三 简约深刻，促进数学思维大提升

翻开本书目录，“建议将‘分数的基本性质’直称为‘分数的相等性质’”“小数容易分数难，何必死死捆绑在一起”“面积测量的活动有点‘故弄玄虚’”等题目，让我一下子感觉，在直白简约的文字背后，既挠到了小学教学中有为思维而思维的“痒”处，又触及了数学的本质，对于培养学生数学核心素养，促进数学思维的提升具有画龙点睛的作用。

张教授认为，小学数学并不简单，甚至具有很高的学术含量。如果仅就一些教育理念进行教学设计是走不远的，许多内容必须从数学本质的揭示上进行梳理，才能设计出更符合学生思维发展的教学案例。像面积，很多教科书上的定义是“物体表面或封闭图形的大小就是它们的面积”，而张教授则从日常生活经验出发，分析得出，面积和长度一样，是人与生俱来的直觉，其实质是用某一个小正方形的面积作为“1”，去度量平面或曲面上一块区域大小的“数”，可以通过“把一个图形用单位方格子填满，再数出一共有多少个方格子，就知道它的面积是几”，用这样“数一数”的办法求面积的大小。

根据这样的思路，我沿着“建立面的概念：抚摸课桌、书本、黑板等物体的面”→“面有大有小：给大小显著不同的两个空白图形涂色比赛”→“多种方法比较面的大小：观察法、重叠法、画格子法”→“统一数据描述标准：用某一个标准（如一个小正方形格子）去度量面，把面的大小用数据描述出来”→“形成面积概念：把标准看作‘1’，这种新的计量即为‘面积’”的逻辑脉络，凸显面积的计量意义。毫无疑问，这样的教学过程是对传统教学的一次突破和超越，比简单地围绕教科书上的面积定义，紧扣“表面”“封闭”等字眼，更能深刻揭示面积的数学意义，更有利于学生数学思维的培养，且为后面平面图形面积的计算奠定了坚实的基础。画1 个方格子看作“1”的数学思想，在学习体积的时候同样能用，这样的数学思想，将来学微积分时也能用上。