分数在教科书中的不同意义（下）

◇林碧珍

（上接第4 期第8 页）

（三）分数是两数相除的结果（商）。

表1

部分-整体关系是将整体量1 个单位（如1盒、1 颗、1 条、1 个）进行等分，描述其中的1 份或几份。若整体量超过1 个单位，如“3 条巧克力平均分给4 人，每人分到几条巧克力”，此问题的整体量是3 条巧克力，超过1 个单位（1 条）。本质上，这是一个等分除问题，列式为3÷4。在三年级，除法意义的教学是通过平均分或分装的操作活动，建立整数中余数比除数小的除法原理。因此，依据之前的学习经验，无法用一个整数表示3÷4 的商，所以需要扩充分数的意义，以分数表示3÷4的商。 若要解决3÷4 的结果是多少这一问题，依据表1 中的图形，学生很容易误以为整体单位量是12 等份，从而写出错误的答案条而非条。当学生犯此错误时，教学时至少有两种补救策略：（1）利用部分-整体关系，以认知冲突教学策略让学生了解“条是将1 条巧克力等分成12 份，但图示中是将1 条巧克力等分成4 份”，从而产生认知冲突；（2）利用单位分量的累加，进一步问学生：“3 个条巧克力合起来是几条巧克力？”

教材中扩张了分数第三种意义，即分数是两数相除的结果，另一个功能是进行分数和小数的互化。 学生之前建立的分数和小数的互化是单纯为了引入纯小数，即分母为10、100 等的分数与小数的互化，如=0.1，=0.01。若要解决任意分数与小数的互化问题，则需借助等值分数将分母扩分为10、100 等来求得，如图7（a）。这样做，不仅计算烦锁，缺乏效率，而且并非所有的分母都可以扩分为10、100 等，故需要借助=b÷a（a≠0）算出其商为小数。

如图7（b），三年级时学习整数除法，会出现其商是整数且余数小于除数的情形。一旦学习一位、两位小数之后，当学习小数的除法问题时，需要将个位上的数转化为十分位或百分位上的数，继续使用除法原理求出商。

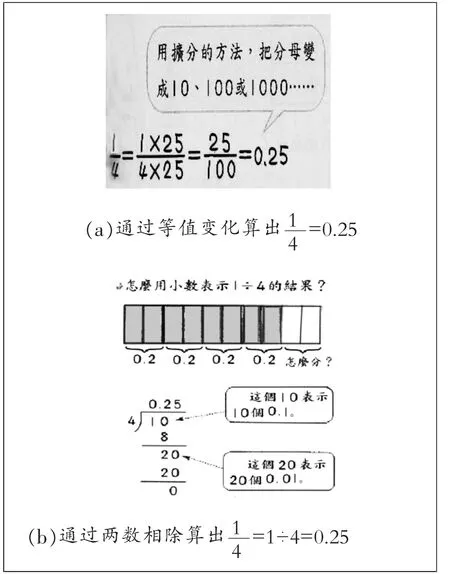
图7

（四）分数是数线上一点表示的数。

分数数线和整数数线一样，都具有数线构成的三要素：随意取一点作为原点（表示的数为0），取适当的长当作一个单位长（如1 厘米或厘米）使得间距都一样，箭头指明向右为正方向。数线具有的特性包含：（1）任何一个数都可以在数线上找到唯一的对应点，这个数就表示该点与原点的距离；（2）数线上任何一个点都可以根据其与原点的距离用唯一的数（实数）表示；（3）对于任意两个数，都可利用它们在数线上对应的点的位置及其与原点的距离来讨论大小关系；（4）在数线上，较大数对应的点，落在较小数对应的点的右边。 数线和线段图的意义不同。线段图是一种解题工具或解题的表征，线段图不需具有方向性，也不需标示原点，其上两点之间的距离表示的仅仅是一个示意长度。

将数线上0~1 这一段等分成若干段，并用分数标示其中任何一等分点，对学生来说难度不大，如图8 中的点A，表但若要在图8 上标示点B 和C 表示的数，对学生来说比较困难，如学生可能在点B 处标示错误答案（12 份中的6 份），在点C 处标示错误答案。

图8

（五）分数是运算子。

运算子（operator）是一种操作或函数。分数运算子是对某量进行缩小倍数或放大倍数的转换。缩小就是对某量进行真分数倍的转换，放大就是对某量进行假分数倍的转换。运算子所描述的分数不带单位，例如：“1 箱牛奶20 瓶，1 箱的是多少瓶牛奶”，其中的不带单位。虽然问题 “1 箱牛奶20 瓶，1 箱的是多少瓶牛奶”和“1 箱牛奶20 瓶，箱是多少瓶牛奶”的整体量都是1 箱，但前者是分数的运算子意义，后者是分数的部分-整体意义。

在教材发展的脉络上，为了解决乘数是真分数的乘法问题，需用到“全部的几分之几”这样的分数倍语言描述，因此必须扩张分数的意义——运算子。乘数是分数的乘法在教材中第一次出现时，分数不带单位，如图9。

图9

对学生而言，解决乘数为分数的乘法问题时，可能只看关键词“……的几分之几”就以乘法计算，出现疑问11 的根源是学生无法理解题目中“1 箱的”的意义。乘数为真分数的乘法问题是学生第一次接触乘数小于1 从而乘的结果变小的乘法问题，这类问题开始挑战学生之前建立的“乘法运算越乘越大”的经验。如对于问题“1 箱牛奶20 瓶，1 箱的是多少瓶牛奶”，学生为了使结果变小，而错误地使用除法算式“20÷=15”来记录该数学问题及答案。因此在进入“乘数小于1”的分数乘法教学单元时，教师必须帮助学生首先理解：（1）乘数为分数时，乘的结果会变小；（2）从“箱”这样的语言转换到“1 箱的”。 图10 是帮助学生从 “1 箱牛奶20瓶，箱是多少瓶牛奶”转换到“1 箱牛奶20 瓶，1 箱的是多少瓶牛奶”的教学历程。

（六）分数是两量的比值。

两量的比值是小学教材中分数的第六种意义。两量的比值所描述的分数倍和运算子一样，分数不带单位；但是其最大不同之处在于两量的比值中的两量可以不具有包含关系，而运算子表示对某量进行缩小倍数或放大倍数的转换。

小学不同年级的教材中，有些句子如“3 的4 倍是12”“12 是3 的倍数”“哥哥的钱是全部的倍”“哥哥的钱是弟弟的倍”，虽然都含有“倍”字，但其意义不同。“3 的4 倍是12”是在二年级建立乘法基本概念时出现的，3 的4 倍表示3 有4 个或4 个3 连加。“12 是3 的倍数” 表示12 可以被3 整除，或3 是12 的因数，是因数和倍数单元的学习内容。“哥哥的钱是全部的倍”是分数的运算子意义，哥哥的钱是全部金额的一部分。“……全部的几分之几倍” 这种语言常出现在比率单元及分数的乘法单元。 小学阶段最晚引入的分数意义是两量的比值，如“哥哥的钱是弟弟的倍”。两量的比值是比较量与基准量两个量的比值（哥哥的钱∶弟弟的钱的比值），当基准量弟弟的钱为1 时，哥哥的钱是弟弟的倍，也就是说，当弟弟的钱是40 元时，哥哥的钱是30 元；当弟弟的钱是100 元时，哥哥的钱是75 元。

以上探讨并分析了台湾教科书中在小学阶段不同年级分数的各种不同意义，将其进行比较与对照，如表2。

四、对分数教学的建议

数系从正整数扩展到负整数、分数、小数、有理数、无理数、实数、虚数、复数，有其发展脉络及需求。同样地，在小学教材中，分数从一种意义扩展到另一种意义也有其发展脉络，以及其扮演的角色与必要性。从本质上说，这六种不同意义对应不同的数学语言。教材中使用的分数语言造成学生分数学习困难的成分可能比分数类型（如真分数、假分数、带分数）的影响还要大。学生解决应用问题比解决计算问题困难许多，教师习惯上将原因归咎于学生的语文程度不佳。然而，从上面的分析可以看出，分数不同的意义在知识本质上本身就具有不同的复杂度和难度，这是造成学生分数学习困难的重要成因。期望根据本文的分析，我们能找到有效的教学策略，陪伴学生一起谨慎对待每个分数语言的意义及其之间的转化。

表2

除了理解分数的多重意义，有效的教学策略是利用生活情境问题帮助学生理解分数不同意义的差异性，或厘清学生理解分数计算法则背后的意义。如对于本文开头的疑问1～8，只要回到原问题情境帮助学生理解什么东西被分，就能厘清这些疑问。 对于疑问13，只要回到原问题情境，即可帮助学生厘清并理解为何（4 个）÷（2个）=2。